Attention Mechanism 최적화와 KV Cache 계산

Introduction

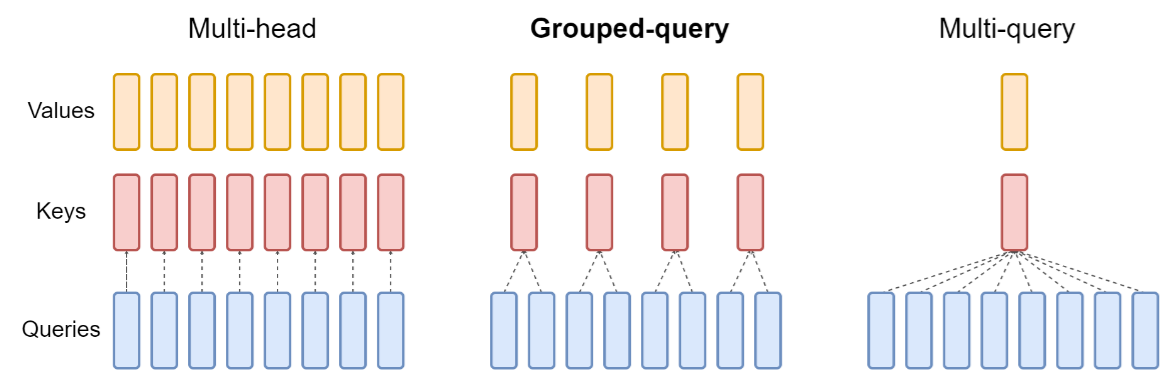
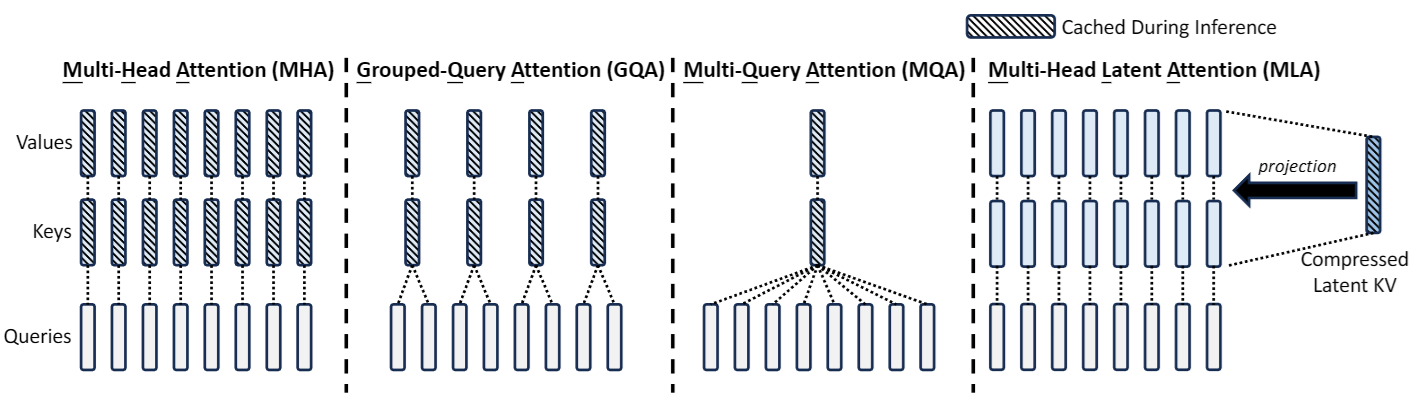
기존의 SDPA(Scaled Dot Product Attention)를 효율화하는 여러가지 방법이 있다. 대표적으로 [1] 에도 나오는 MHA(Multi-Head Attention)부터 시작해서, MQA(Multi-Query Attention), GQA(Grouped-Query Attention), 그리고 MLA(Multi-head Latent Header Attention)에 대해 알아보고 KV Cache가 얼마나 optimize되는지 알아보고자 한다.

SDPA (Scaled Dot Product Attention)

Attention 메커니즘이야 워낙 유명하고 예전에도 이에 대한 글을 쓴 적이 있다.

• \(\textrm{batch\_size}\): 배치 사이즈
• \(\textrm{seq}\): sequence length
• \(d_{\textrm{model}}\): 모델의 hidden representation size. hidden_size

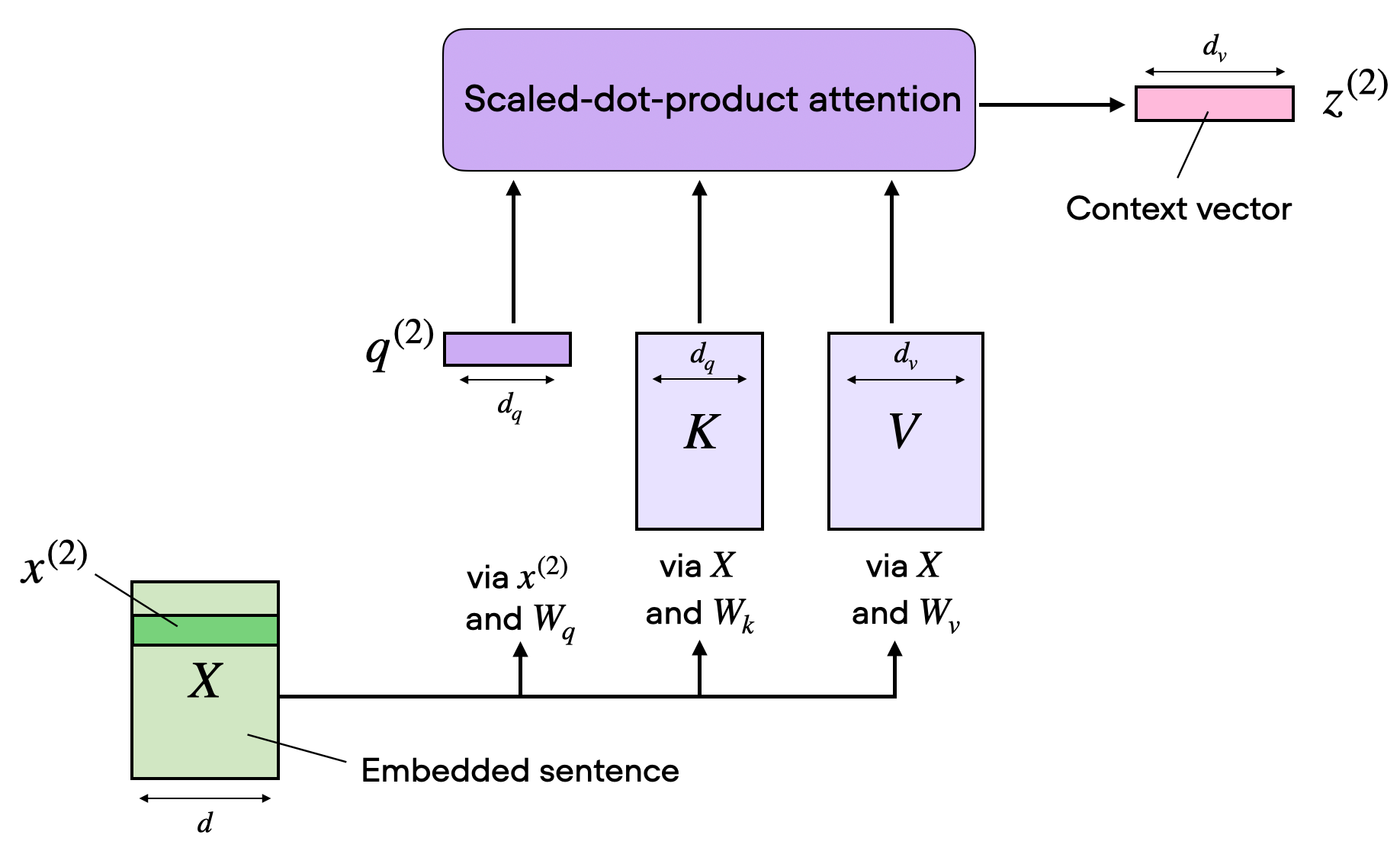
Multi Head를 고려하지 않는다고 가정하자. Input $X$가 \(\textrm{batch\_size} \times \textrm{seq} \times d_{\textrm{model}}\)일 때, 모델이 실질적으로 훈련하는 weight matrix $W^Q$, $W^K$, $W^V$는 각각 다음과 같은 dimension을 가진다.

\[W^Q \in \mathbb{R}^{d_{\textrm{model}} \times d_{\textrm{model}}}\] \[W^K \in \mathbb{R}^{d_{\textrm{model}} \times d_{\textrm{model}}}\] \[W^V \in \mathbb{R}^{d_{\textrm{model}} \times d_{\textrm{model}}}\]

이는 $Q, K, V$는 BMM(batch matrix-matrix product)을 통해 다음과 같은 dimension을 가짐을 뜻한다.

\[Q = X W^Q \in \mathbb{R}^{\textrm{batch\_size} \times \textrm{seq} \times d_{\textrm{model}}}\] \[K = X W^K \in \mathbb{R}^{\textrm{batch\_size} \times \textrm{seq} \times d_{\textrm{model}}}\] \[V = X W^V \in \mathbb{R}^{\textrm{batch\_size} \times \textrm{seq} \times d_{\textrm{model}}}\]

Attention score \(Q K^\mathsf{T}\)는 다음과 같이 계산되고,

\[Q \in \mathbb{R}^{\textrm{batch\_size} \times \textrm{seq} \times d_{\textrm{model}}}\] \[K^T \in \mathbb{R}^{\textrm{batch\_size} \times d_{\textrm{model}} \times \textrm{seq} }\] \[Q K^\mathsf{T} \in \mathbb{R}^{\textrm{batch\_size} \times \textrm{seq} \times \textrm{seq} }\]

Attention weight \(\textrm{Softmax}\left(\dfrac{QK^T}{\sqrt{d_k}}\right)\) 또한 \(Q K^\mathsf{T}\)와 같은 dimension을 가진다.

\[\textrm{Softmax}\left(\dfrac{QK^T}{\sqrt{d_k}}\right) \in \mathbb{R}^{\textrm{batch\_size} \times \textrm{seq} \times \textrm{seq} }\]

이렇게 구해진 Attention weight \(Q K^\mathsf{T}\)는 일종의 가중치 역할을 하며 이를 \(V\)와 곱해서 Attention output을 생성하게 된다. Attention output 은 다음과 같다.

\[\textrm{Attention}(Q,K,V) = \textrm{Softmax}\left(\dfrac{QK^T}{\sqrt{d_k}}\right)V \in \mathbb{R}^{\textrm{batch\_size} \times \textrm{seq} \times d_{\textrm{model}} }\]

이 뒤에 layernorm이나 FC(Fully Connected) Layer등의 이야기는 생략한다.

Summarizing the self-attention mechanism

MHA (Multi-Head Attention)

MHA를 하는 이유는 “아 다르고 어 다르다”라는 속담을 생각하면 쉽다. 같은 표현이라도 다른 의미로 받아들여질 수 있도록 모델을 학습시키기 위함이다. MHA를 통해 모델은 입력의 다양한 위치에 대해 더 풍부하게 이해할 수 있게 된다.

Head를 사용하는 가장 기본적인 방법으로, [1]에 나와있는 방법이다.

추가되는 파라미터는 다음과 같다.

• \(d_{\textrm{head}}\): attention head의 사이즈
• \(n_{\textrm{head}}\) : Attention head 수 num_attention_heads

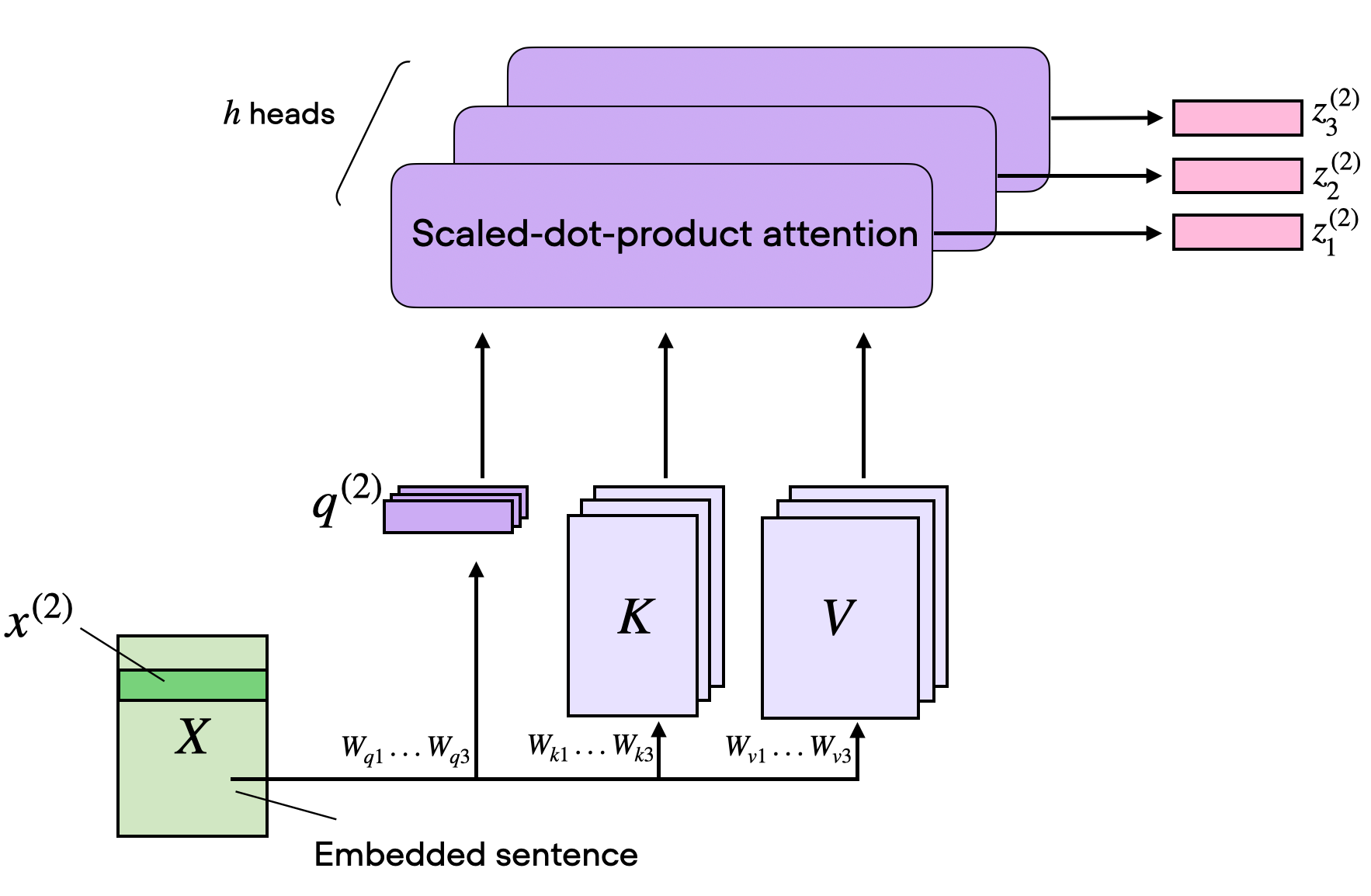
\(d_{\textrm{model}}\)을 \(n_{\textrm{head}}\)개의 head로 쪼개서 학습시킨다고 보면 된다. [1]에서는 $n_{\textrm{head}}=8$로 놓고 병렬적으로 계산하도록 하였다. \(d_{\textrm{head}} = d_{\textrm{model}} / n_{\textrm{head}}\)으로 정의하므로, 계산량은 같다. 원래 512개의 \(d_{\textrm{model}}\)을 사용하던걸 \(d_{\textrm{head}} = 64\)을 $n_{\textrm{head}}=8$ 번 수행하는 것이다.

일반화를 위해 $Q, K, V$에 대해 헤드를 분리해서 다음과 같이 표현한다. MHA에서는 \(n_{\textrm{head}}\)가 고정이므로 \(d_q = d_k = d_v\)이다.

• \(d_q\): 각 attention head에서의 query vector 사이즈
• \(d_k\): 각 attention head에서의 key vector 사이즈
• \(d_v\): 각 attention head에서의 value vector 사이즈
• \(n_{\textrm{head}}\): Attention head 수 num_attention_heads

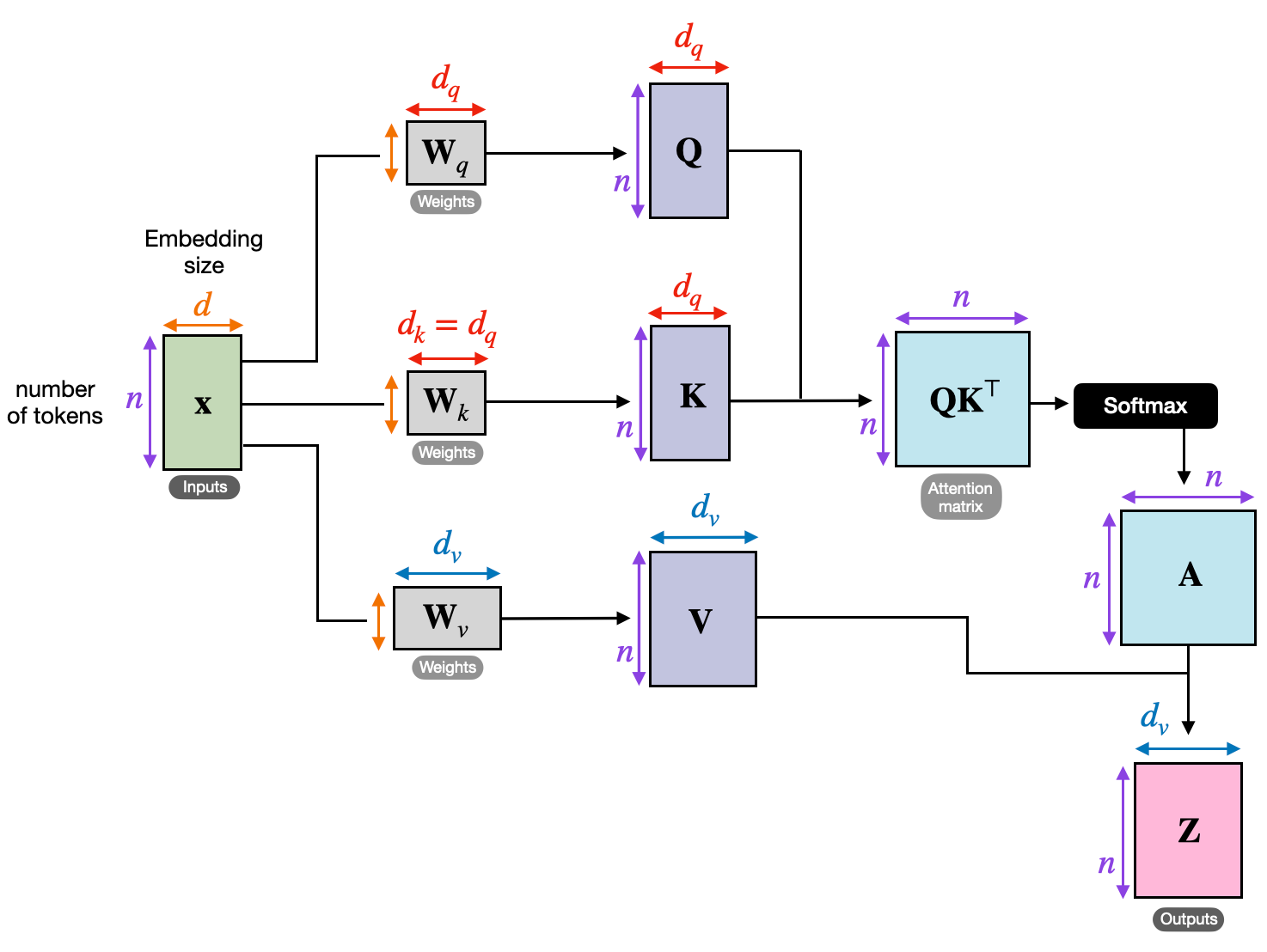
Input $X$가 \(\textrm{batch\_size} \times \textrm{seq} \times d_{\textrm{model}}\)일 때, weight matrix $W^Q$, $W^K$, $W^V$는 $d_q, d_k, d_v$에 의해 다음과 같이 변한다.

\[W^Q \in \mathbb{R}^{d_{\textrm{model}} \times d_q}\] \[W^K \in \mathbb{R}^{d_{\textrm{model}} \times d_k}\] \[W^V \in \mathbb{R}^{d_{\textrm{model}} \times d_v}\]

$Q, K, V$는 다음과 같이 변한다.

\[Q = X W^Q \in \mathbb{R}^{\textrm{batch\_size} \times \textrm{seq} \times d_q}\] \[K = X W^K \in \mathbb{R}^{\textrm{batch\_size} \times \textrm{seq} \times d_k}\] \[V = X W^V \in \mathbb{R}^{\textrm{batch\_size} \times \textrm{seq} \times d_v}\]

여기서 \(Q K^\mathsf{T}\)를 연산하기 위해서는 \(d_q = d_k\)라는 조건이 필요하고 해당 조건이 맞다고 하면, \(Q K^\mathsf{T}\)는 다음과 같이 계산된다.

\[Q K^\mathsf{T} \in \mathbb{R}^{\textrm{batch\_size} \times \textrm{seq} \times \textrm{seq} }\]

각 head의 attention output은 다음과 같다.

\[\textrm{head}_i = \textrm{Attention}(Q,K,V) = \textrm{Softmax}\left(\dfrac{QK^T}{\sqrt{d_k}}\right)V \in \mathbb{R}^{\textrm{batch\_size} \times n_{\textrm{head}} \cdot d_v \times d_{\textrm{model}} }\]

이렇게 각 head별로 계산된 attention을 concat으로 계산하면

\[\textrm{MultiHead}(Q,K,V) = \textrm{Concat}(\textrm{head}_1, \dots, \textrm{head}_i) W^O \in \mathbb{R}^{\textrm{batch\_size} \times \textrm{seq} \times n_{\textrm{head}} \cdot d_v}\]

가 되고 여기서 \(W^O\)만 다음과 같은 dimension을 가진다.

\[W^O \in \mathbb{R}^{n_{\textrm{head}} \cdot d_v \times d_{\textrm{model}}}\]

Multi-head attention: self-attention with multiple heads

\(d_q = d_k\)이어야 하지만, \(d_v\)는 다를 수는 있다. [1] 논문에서는 \(d_q = d_k = d_v = d_{\textrm{model}} / n_{\textrm{head}} = 64\)를 사용하였으나, 어차피 \(Q K^\mathsf{T}\)는 \(\textrm{batch\_size} \times \textrm{seq} \times \textrm{seq}\)의 차원을 가지므로, \(V\)와 차원을 무관한 차원을 가져도 된다. 따라서, 아래 그림과 같이 $d_v$를 다르게 하고 사용해도 된다.

Multi-head attention: focused on the matrix dimensions

또한 결과적으로 head 수 만큼 쪼개서 계산하는 것뿐이므로 기존의 SDPA와 연산량 자체는 동일하다.

KV Cache

KV Cache는 Autoregressive Decoder 모델에서 효율적인 계산을 위해 사용하는 기법으로, Self-Attention의 계산 비용을 줄이는 데 중요한 역할을 한다. 이를 이해하기 위해 먼저 MHA의 계산 구조와 비용을 살펴보겠습니다.

SDPA이나 MHA이나 계산비용은 같으므로 MHA기준으로 설명해본다면 다음과 같은 프로세스를 거친다.

1. batch_size를 무시할 때, 입력 시퀀스 \(\textrm{seq}\)에서 매번 \(Q, K, V\)를 계산하게 된다.
2. \(Q K^\mathsf{T}\)를 내적을 통해 계산하여 \(\textrm{seq} \times \textrm{seq}\)의 행렬을 생성한다.
3. Softmax를 적용하여 attention score를 계산한다.
4. Attention score를 \(V\)와 곱해 Attention output을 생성한다.

KV Cache를 적용하지 않았을 때의 계산 비용

1. \(Q K^\mathsf{T}\) 내적 계산 비용 Decoder only model이라 가정할 때, \(Q\)가 현재 디코더 스텝 $t$의 쿼리 벡터이고, \(K\)와 \(V\)는 이전 디코더 스텝의 출력을 기반으로 계산된다. \(T\)를 전체 시퀀스 길이(\(\textrm{seq}\)), \(d_k\)를 Key/Query 벡터의 차원으로 가정하면,

   \[Q K^\mathsf{T} \in \mathbb{R}^{(T \times d_k) \cdot (d_k \times T)}\]

   이는

   \[Q K^\mathsf{T} \in \mathbb{R}^{T \times T}\]

   로 수렴한다.

   각 내적의 연산은 \(O(d_k)\)이고, 이를 \(T \times T\) 행렬에 수행하게 되므로 \(Q K^\mathsf{T} = O(T^2 \cdot d_k)\)의 비용이 필요하게 된다.

2. Softmax 계산 비용 (attention score 계산비용) \(T \times T\) 행렬의 각 원소에 대해 Softmax 함수를 적용하면 되므로, \(O(T^2)\)이다.

3. Attention output 계산 비용 Attention score 행렬 \(T \times T\)와 \(V\) 행렬 \(T \times d_v\)의 곱이다. 벡터 내적으로 생각해서 계산한다면, 각 원소는 \(O(T)\)만큼 비용이 들고 이를 \(T\times d_v\)만큼 계산해야하므로, 총 계산 비용은 \(O(T^2 \cdot d_v)\)가 필요하다.

4. MHA의 계산 비용 1.부터 3.까지의 계산 비용을 합하면 \(O(T^2 \cdot d_k) + O(T^2) + O(T^2 \cdot d_v)\)이다. 그리고 보통 MHA에서는 $d_k = d_v$로 놓는 경우가 많기 때문에 $d = d_k = d_v$라고 할 수 있다.

   따라서 총합하면 각 query step $t$마다 다음과 같이 계산 비용이 quadratic하게 증가하며, 이를 $d$를 사용하여 근사할 수 있다.

   \[O(t^2 \cdot d_k) + O(t^2) + O(t^2 \cdot d_v) \approx O(t^2 \cdot d)\]

   이를 모든 Step에 대해 누적하면

   \[\sum_{t=1}^T O(t^2 \cdot d) = O (T^3 \cdot d)\]

   즉, sequence length가 길어질 수록 전체 비용이 cubic하게 증가한다.

KV Cache 원리

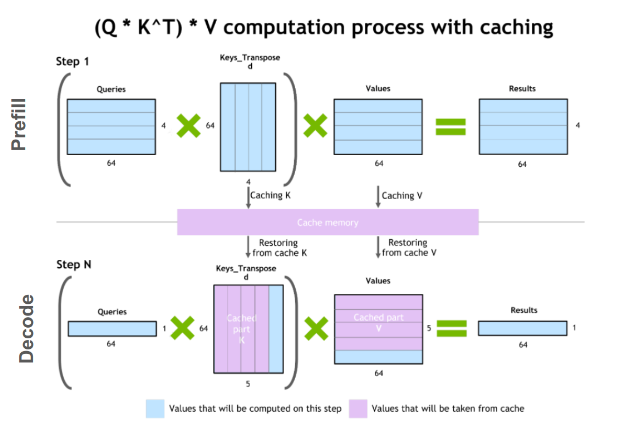
일반적인 Self-Attention에서 \(Q\)는 단일 입력 토큰 (\(x_t\))이라고 생각하면 되고, \(K, V\)는 입력 토큰의 집합인 입력 시퀀스 (\(X=[x_1, x_2, \dots, x_T]\))에 대해서 생성된다. 따라서 입력 시퀀스에 대해 계산된 \(K, V\)를 매 \(Q\)마다 모두 다시 계산할 필요가 없다.

이를 Decoder only 모델에 대해서도 다시 생각해보자면, Query라는건 decoder step에서의 신규 토큰, Key는 모델이 “attend”해야할 기존 context, Value는 이전 context에 대한 가중치합(weighted sum)라고 할 수 있다.

이 때, 이전 스텝에서 사용한 Key, Value는 유지하면서 신규 토큰에 대해서만 계산하고 \(T\)쪽 차원을 점진적으로 늘리면 계산 비용을 아낄 수 잇다.

An illustration of the key-value caching mechanism

KV Cache를 적용할 때의 계산 비용

Autoregressive한 Decoder only 모델에서도 전체 타입스텝에 대해 누적하면 \(O(T^2 \cdot d)\)의 계산 비용이 필요하다. 하지만, KV Cache를 사용하는 순간 다음과 같이 계산비용이 감소하게 된다.

1. \(Q K^{\mathsf{T}}\) 내적 계산 비용 기존에는 \(Q K^{\mathsf{T}} \in \mathbb{R}^{T \times T}\)를 전부 계산했다면, 이제는 신규 query 토큰 \(q_k\)와 \(K_{\textrm{past}}\)의 내적만 계산하면 된다.

   \[q_t K^\mathsf{T} \in \mathbb{R}^{(1 \times d_k) (T_{\textrm{past}} \times d_k)^\mathsf{T}}\]

   따라서 비용은 \(O(T_{\textrm{past}} \cdot d_k)\)이다.

2. Softmax 계산 비용 (attention score 계산비용)

   \(q_t\)에 대해 Softmax를 적용하므로 비용은 다음과 같이 감소한다.

   \[O(T_{\textrm{past}})\]

3. Attention output 계산 비용

   새로운 attention score와 \(V_{\textrm{past}}\)의 곱으로 계산되며, \(V_{\textrm{past}}\in\mathbb{R}^{T_{\textrm{past}} \times d_v}\) 이므로, 다음과 같이 계산된다. \(\textrm{Softmax}\left(\dfrac{Q K^\mathsf{T}}{\sqrt{d_k}}\right) V \in \mathbb{R}^{(1 \times T_{\textrm{past}})} \mathbb{R}^{T_{\textrm{past}} \times d_v}\)

   따라서 계산 비용은 다음과 같다.

   \[O(T_{\textrm{past}}) \cdot d_v\]

4. MHA의 계산 비용 따라서 총합하면 각 query step $t$마다 다음과 같이 linear하게 계산 비용이 증가하고,

   \[O(t_{\textrm{past}} \cdot d_k) + O(t_{\textrm{past}}) + O(t_{\textrm{past}} \cdot d_v) \approx O(t_{\textrm{past}} \cdot d)\]

   이를 모든 시퀀스에 대해 종합하면, 전체 time step에 대해 quadratic한 계산 비용이 든다.

   \[\sum_{t=1}^T O(t \cdot d) = O(T^2 \cdot d)\]

MQA (Multi-Query Attention)

이렇게 $K$와 $V$를 재활용하는 것이 중요해지자, 아예 Key와 Value를 여러개의 head로 만드는 것이 아닌, 하나의 Key Value로 공유하자는 아이디어가 나왔다. [2]

기존의 MHA와 MQA를 비교하면 다음 그림의 맨 왼쪽과 오른쪽 그림을 비교하면 된다. Query는 유지되지만, Key와 Value는 하나임을 알 수 있다.

A comparison of different attention mechanisms. (MHA, GQA, MQA)

MHA에서는 전체 시퀀스 \(T\)에 대해 각 head $i$에 대한 \(Q_i, K_i, V_i\)는 다음과 같았다.

\[\mathbf{Q}_i \in \mathbb{R}^{T \times d_k}, \mathbf{K}_i \in \mathbb{R}^{T \times d_k}, \mathbf{V}_i \in \mathbb{R}^{T \times d_v}\] \[\begin{align} \textbf{head}_i &= \textrm{Attention} (\mathbf{Q}_i, \mathbf{K}_i, \mathbf{V}_i) \\ \textrm{MHA}(Q, K, V) &= \textrm{Concat}(\textbf{head}_1, \dots, \textbf{head}_{n_{\textrm{head}}})W^O \end{align}\]

그러나, MQA에서는 다음과 같이 변화한다.

\[\mathbf{Q}_i \in \mathbb{R}^{T \times d_k}, \mathbf{K}_\textrm{shared} \in \mathbb{R}^{T \times d_k}, \mathbf{V}_\textrm{shared} \in \mathbb{R}^{T \times d_v}\] \[\begin{align} \textbf{head}_i &= \textrm{Attention} (\mathbf{Q}_i, \mathbf{K}_\textrm{shared}, \mathbf{V}_\textrm{shared}) \\ \textrm{MQA}(Q, K, V) &= \textrm{Concat}(\textbf{head}_1, \dots, \textbf{head}_{n_{\textrm{head}}})W^O \end{align}\]

\(\mathbf{Q}_i\)는 결국 \(n_{\textrm{head}}\)만큼 계산량이 늘어나지만, \(\mathbf{K}_\textrm{shared}\)와 \(\mathbf{V}_\textrm{shared}\)는 공유되기 때문에 매우 적은 메모리로도 decoding을 할 수 있게 되었다. 적은 KV cache로 메모리 부담을 줄이고 inference 속도를 향상시킬 수 있게 된 것이다.

그러나, 하나의 key와 value를 사용하기 때문에 MHA보다는 표현력을 학습하는데 있어 일부 떨어질 수 밖에 없다.

GQA (Grouped Query Attention)

[3] 에서는 위 MQA의 문제점을 해결하기 위해 MHA와 MQA의 절충안을 제시했다.

다음 그림의 가운데가 GQA이다. MQA처럼 하나의 Key Value를 쓰지는 않지만, 그렇다고 MHA처럼 헤드 개수만큼 만들지도 않는다. 일종의 그룹을 만들어서 $K, V$를 사용하는 방법으로 메모리 사용량도 줄이고 표현력도 잘 학습될 수 있도록 한 것이다.

A comparison of different attention mechanisms. (MHA, GQA, MQA)

$K$와 $V$를 위해 각 헤드 $i$대신 $g(i)$라는 group index를 도입하였다. \(n_{\textrm{head}}\)를 $G$개의 그룹으로 만든 것이다. GQA에서는 $\mathbf{Q}, \mathbf{K}, \mathbf{V}$를 각 헤드 $i$나 $g(i)$에 대해서 다음과 같이 표현할 수 있다.

\[\mathbf{Q}_i \in \mathbb{R}^{T \times d_k}, \mathbf{K}_{g(i)} \in \mathbb{R}^{T \times d_k}, \mathbf{V}_{g(i)} \in \mathbb{R}^{T \times d_v}\] \[\begin{align} \textbf{head}_i &= \textrm{Attention} (\mathbf{Q}_i, \mathbf{K}_\textrm{g(i)}, \mathbf{V}_\textrm{g(i)}) \\ \textrm{GQA}(Q, K, V) &= \textrm{Concat}(\textbf{head}_1, \dots, \textbf{head}_{n_{\textrm{head}}})W^O \end{align}\]

만약 $G$가 1이면 MQA를 $G$가 \(n_{\textrm{head}}\)이면 MHA를 표현할 수 있게 되었다. 이 방법은 Llama 3 모델에 적용되어 8B 모델이 Llama 2의 7B 모델과 유사한 inference 효율에 기여함을 보여주었다. [4]

MLA (Multi-head Latent Attention)

[5]에서는 LoRA의 아이디어를 빌려온 Low-Rank Key-Value Joint Compression을 개발하였다. 이는 Key와 Value 매트릭스를 캐싱하는 대신에, low rank vector인 $C^{KV}$에 압축된 형태로 표현한다.

A comparison of different attention mechanisms. (MHA, GQA, MQA, MLA)

$K$와 $V$를 새로운 low rank vector인 $c^{KV}_t \in \mathbb{R}^{d_c}$에 대해 표현하면 다음과 같다. 이 때, 새로운 차원 \(d_c \ll d_h n_{\textrm{head}}\)은 KV compression dimension이며 기존 head를 사용할 때의 차원보다 매우 작기 때문에 효율적이다.

\(\begin{align} c^{KV}_t &= W^{DKV} \mathbf{h}_t \\ \mathbf{k}^C_t = W^{UK} c_t^{KV} \\ \mathbf{v}^C_t = W^{UV} c_t^{KV} \\ \end{align}\) 이 때, \(W^{DKV} \in \mathbb{R}^{d_c \times d}\)는 key-value에 대한 down-projection matrix ($D$)를, \(W^{UV},W^{UK} \in \mathbb{R}^{ d_h n_{\textrm{head}} \times d_c}\)는 key-value에 대한 up-projection matrix ($U$)를 나타낸다.

Deepseek-V2 논문에서는 모델 훈련 과정에서의 activation memory를 줄이기 위해서 query에 대해서도 비슷한 접근을 취하였다.

\[\begin{align} c^{Q}_t &= W^{DQ} \mathbf{h}_t \\ \mathbf{q}^C_t = W^{UQ} c_t^{Q} \end{align}\]

마찬가지로 query compression vector \(c^Q_t \in \mathbb{R}^{d^{\prime}_c}\)는 query compression dimension \(d^{\prime}_c (\ll d_h n_{\textrm{head}})\) 을 가진다. 또한, down-projection matrix와 up-projection matrix도 \(W^{DQ}\in\mathbb{R}^{d^{\prime}_c \times d}\), \(W^{UQ} \in \mathbb{R}^{d_h n_{\textrm{head}} \times d^{\prime}_c}\) 의 차원을 가진다.

RoPE decoupling

하지만 이렇게 되면 RoPE(Rotary Position Embedding)을 적용하기가 까다로워진다. 왜냐하면, RoPE는 key와 query의 위치에 따라 결정되기 때문이다.

이를 해결하기 위해서 RoPE를 위한 헤드별 추가적인 $Q$와 $K$ 벡터를 생성한다. 이 때 RoPE를 위해 decoupled된 dimension을 \(d^R_h\)라고 하면, 추가적으로 생성되는 query와 key 벡터는 \(\mathbf{q}^R_{t,i} \in \mathbb{R}^{d^R_h}\)와 \(\mathbf{k}^R_{t,i} \in \mathbb{R}^{d^R_h}\)라고 표현할 수 있다.

\(\mathbf{q}^R_{t,i}\)와 \(\mathbf{k}^R_{t,i}\)는 기존에 만들어진 압축된 \(\mathbf{q}^C_{t,i}\)와 \(\mathbf{k}^C_{t,i}\)와 concat되어서 query와 key로 사용되게 된다.

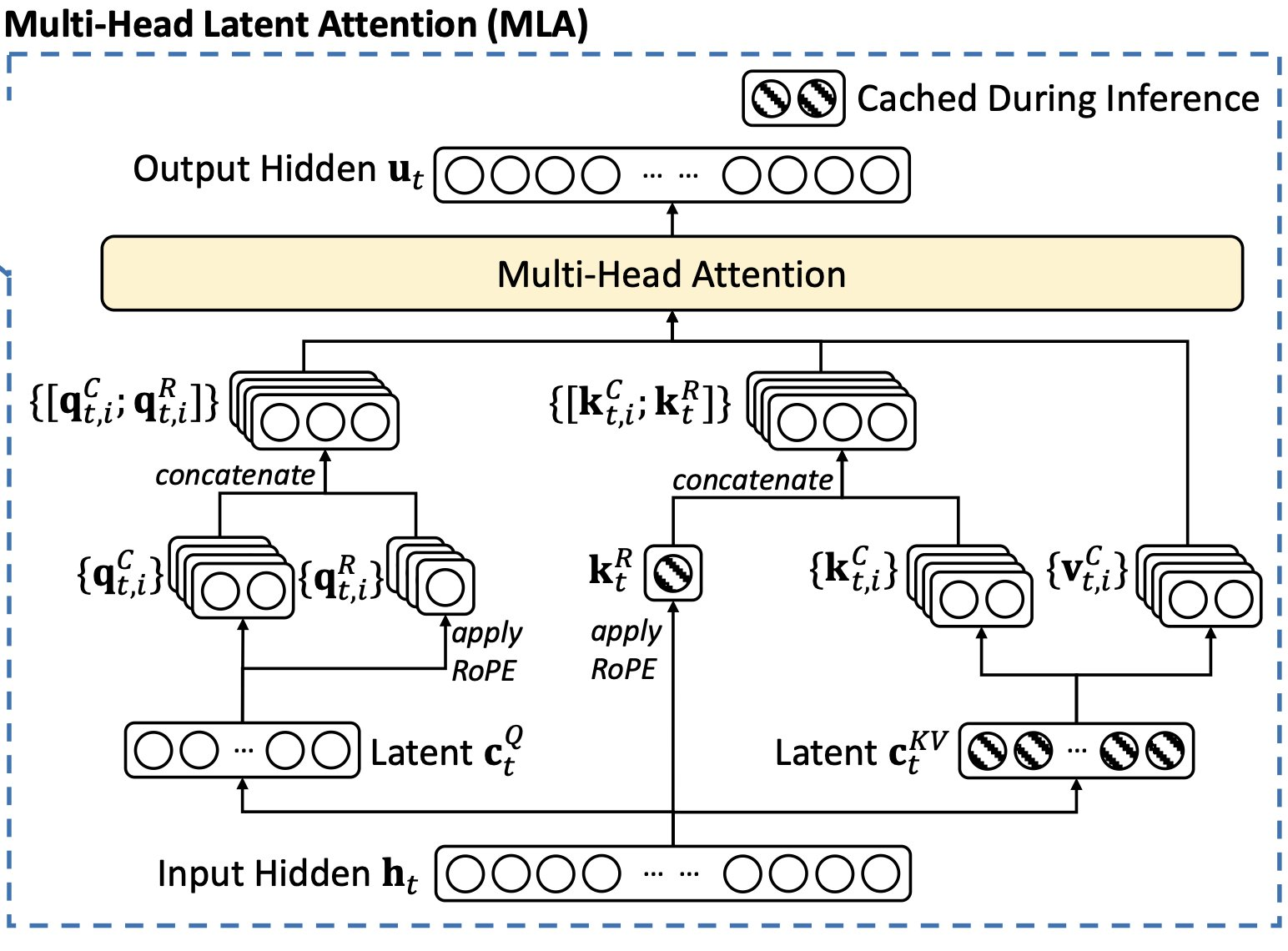
\[\begin{align} [\mathbf{q}^R_{t,1}; \mathbf{q}^R_{t,2}; \dots; \mathbf{q}^R_{t,i}] = \mathbf{q}^R_t &= \textrm{RoPE}(W^{QR}c^Q_t) \\ \mathbf{k}^R_t &= \textrm{RoPE}(W^{KR}h_t) \\ \mathbf{q}_{t,i} &= [\mathbf{q}^C_{t,i};\mathbf{q}^R_t] \\ \mathbf{k}_{t,i} &= [\mathbf{k}^C_{t,i};\mathbf{k}^R_t] \\ \mathbf{o}_{t,i} &= \sum_{j=1}^t \textrm{Softmax}_j \left( \dfrac{\mathbf{q}_{t,i}^T \mathbf{k}_{t,i}}{\sqrt{d_h + d^R_h}} \right) \mathbf{v}^C_{j,i} \\ \mathbf{u}_t &= W^O [\mathbf{o}_{t,1};\mathbf{o}_{t,2}; \dots; \mathbf{o}_{t,n_{\textrm{head}}}] \end{align}\]

이 때, \(W^{QR}\in\mathbb{R}^{d^R_h n_{\textrm{head}} \times d^{\prime}_c}\)와 \(W^{KR}\in\mathbb{R}^{d^R_h n_{\textrm{head}} \times d}\)는 RoPE를 MLA와 decoupling하기 위해 만든 weight matrix이다.

따라서 RoPE를 적용했을 경우 캐싱되는 것은 \(c^{Q}_t\) 뿐만 아니라 \(\mathbf{k}^R_t\)도 포함한다.

모든 과정은 다음 그림에서 확인할 수 있다.

Details of MLA

TPA(Tensor Product Attention)

이 논문은 아직 자세히 읽어보지 않았지만, 지금까지의 MHA, MQA, GQA, MLA에 대한 정리를 잘해서 읽기 좋다. [6]

KV Cache 메모리 크기 구하기

그럼 과연 KV Cache는 얼마나 필요할까? 심플하게 MHA라고 가정해보자.

각 헤드별 $K$와 $V$는 다음과 같이 위에서 정의하였다.

\[K = X W^K \in \mathbb{R}^{\textrm{batch\_size} \times \textrm{seq} \times d_k}\] \[V = X W^V \in \mathbb{R}^{\textrm{batch\_size} \times \textrm{seq} \times d_v}\]

batch size도 1이고 토큰 하나에 대해서 생각해보면, 모든 헤드에 대해 생각해야하고, 레이어도 여러개인 경우를 생각해봤을 때 \(K\)와 \(V\)에 대해서는 다음과 같은 메모리가 필요하다.

2 $\cdot$ num_layers $\cdot$ (num_attention_heads $\cdot$ head_dim) $\cdot$ precision_in_bytes

여기서 각 변수는 다음과 같다.

• $2$: $K$와 $V$에 대해서 수행하기 때문에 2를 곱한다.
• num_layers: 레이어수
• num_attention_heads $\cdot$ head_dim: 모델의 차원 (hidden_size)
• precision_in_bytes: sizeof(타입). float16 혹은 bfloat16인 경우 2, float8인 경우 1, float32인 경우 4.

이를 여러개의 토큰과 batch size에 대해 확장할 수 있다.

전체 KV Cache는 다음과 같은 공식이 나온다.

batch_size $\cdot$ sequence_length $\cdot$ 2 $\cdot$ num_layers $\cdot$ (num_attention_heads $\cdot$ head_dim) $\cdot$ precision_in_bytes

• batch_size: 말 그대로 배치 사이즈
• sequence_length: context length를 넣으면 되므로, max_position_embeddings 값을 사용하는게 맞다.

MHA KV Cache 공식

위에서 살펴본 것이 MHA이다.

batch_size $\cdot$ sequence_length $\cdot$ 2 $\cdot$ num_layers $\cdot$ (num_attention_heads $\cdot$ head_dim) $\cdot$ precision_in_bytes

MQA KV Cache 공식

MQA의 경우 하나의 $K$, $V$를 공유한다. 허깅페이스 모델 config.json에 따르면 num_key_value_head=1로 주어진다.

batch_size $\cdot$ sequence_length $\cdot$ 2 $\cdot$ num_layers $\cdot$ (num_key_value_heads $\cdot$ head_dim) $\cdot$ precision_in_bytes

이 때, head_dim = hidden_size // num_attention_heads로 계산된다.

GQA KV Cache 공식

GQA의 경우 num_key_value_head개의 $K$, $V$를 공유한다. 그래서 MQA와 식은 같다.

batch_size $\cdot$ sequence_length $\cdot$ 2 $\cdot$ num_layers $\cdot$ (num_key_value_heads $\cdot$ head_dim) $\cdot$ precision_in_bytes

결론

huggingface model의 config.json의 경우 num_key_value_head라는 변수를 따로 주기 때문에 MHA, MQA, GQA 모두 대응할 수 있다.

다음과 같은 num_key_value_head 조건에 따라 MHA, MQA, GQA가 적용된다.

• MHA: num_key_value_heads=num_attention_heads인 경우
• MQA: num_key_value_heads=1인 경우
• GQA: num_key_value_heads!=1 and num_key_value_heads!=num_attention_heads (else) 인 경우

이에 따라 KV Cache 공식은 다음과 같다. (head_dim = hidden_size // num_attention_heads) 이 때, sequence_length는 보수적으로 context window length(max_position_embeddings)를 따르는게 좋다고 생각한다.

batch_size $\cdot$ sequence_length $\cdot$ 2 $\cdot$ num_layers $\cdot$ (num_key_value_heads $\cdot$ head_dim) $\cdot$ precision_in_bytes

Llama 3 8B 예시

• 컨텍스트 길이 (max_position_embeddings): 8192 (최대 시퀀스 길이)
• 히든 크기 (hidden_size): 4096 (각 토큰이 표현되는 벡터 크기)
• 어텐션 헤드 수 (num_attention_heads): 32 (병렬 어텐션 헤드의 수)
• Key/Value 헤드 수 (num_key_value_heads): 8 (K/V 캐시의 헤드 수)
• 히든 레이어수 (num_hidden_layers): 32
• 데이터 타입 (torch_dtype): bfloat16 (2 바이트 per value)

이에 따라 head_dim = 4096 // 32 = 128이며, batch_size = 1, 최대 context length인 8192을 적용하면, 다음과 같다.

1 $\cdot$ 8192 $\cdot$ 2 $\cdot$ 32 $\cdot$ 8 $\cdot$ 128 $\cdot$ 2 = 1073741824 = 1GB

References

• Mastering LLM Techniques: Inference Optimization (한국어)
• MHA vs MQA vs GQA vs MLA

1. [1]A. Vaswani, “Attention is all you need,” Advances in Neural Information Processing Systems, 2017.
2. [2]N. Shazeer, “Fast transformer decoding: One write-head is all you need,” arXiv preprint arXiv:1911.02150, 2019.
3. [3]J. Ainslie, J. Lee-Thorp, M. de Jong, Y. Zemlyanskiy, F. Lebrón, and S. Sanghai, “Gqa: Training generalized multi-query transformer models from multi-head checkpoints,” arXiv preprint arXiv:2305.13245, 2023.
4. [4]A. Dubey et al., “The llama 3 herd of models,” arXiv preprint arXiv:2407.21783, 2024.
5. [5]A. Liu et al., “Deepseek-v2: A strong, economical, and efficient mixture-of-experts language model,” arXiv preprint arXiv:2405.04434, 2024.
6. [6]Y. Zhang et al., “Tensor Product Attention Is All You Need,” arXiv preprint arXiv:2501.06425, 2025.