Tensor Program II

Introduction

(Yang et al. 2022)와 (Yang, Simon, and Bernstein 2023)를 리뷰하기에 앞서 (Yang 2020)를 살펴보기로 하겠다.

이 논문의 핵심은 NTK를 확장하여 MLP뿐만 아니라 다른 어떤 아키텍처에서도 동일한 이론을 적용할 수 있음을 보인다. NTK가 중요하다는 것은 알고있었지만, 너무 이상적인 이론이라고 생각하고 있었는데, 이 논문을 통해서 많은 궁금증이 풀린 경험이 있기에 소개한다.

(Yang 2019) 논문도 같이 보는게 맞으나, 다음 버전에서 잘 요약해주기도 했다고 생각하기도 하고, 무엇보다 양이 너무 많아서 생략한다.

Neural Tangent Kernel (NTK)

먼저 알아야할 것은 Neural Tangent Kernel(NTK)이다. NTK를 통해 nonlinear한 모델을 linear하게 만들어서 training dynamics를 해석할 수 있는 길이 열렸다고 볼 수 있다.

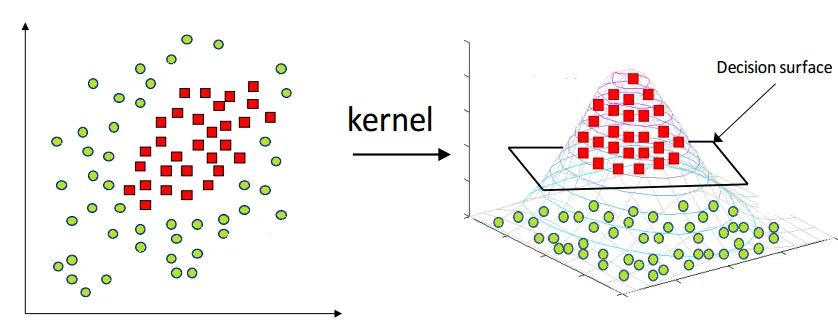
NTK는 이름 그대로 커널(Kernel)이지만, 딥러닝을 이해하는데 있어 중요한 개념이다. 머신러닝에서의 커널이란 고차원의 특성 공간(feature space)로 데이터를 변환하는 함수를 뜻한다. 아래의 그림처럼 2차원에서 linear함수로 분류가 되지 않는 데이터도 3차원으로 변환하면 hyperplane에 의해 분류가 될 수 있음을 알 수 있다. 또한 커널을 이용하면 고차원으로 매핑하지 않고도 내적(inner product)을 간단하게 계산할 수 있는 커널 트릭(kernel trick)을 사용할 수 있게 해준다.

What is the kernel trick? Why is it important?t

NTK는 테일러 전개(taylor expansion)를 통해 무한한 너비(infinite width)를 가지는 simple 2-hidden layer를 랜덤 초기값(initialization)이어도 결정론적(deterministic)인 선형 함수(linear function)로 변환해주는 역할을 수행하는 이론적인 틀이라고 요약할 수 있다. (Jacot, Gabriel, and Hongler 2018)

NTK: Beyond Intuition

(Yang 2020)의 표현에 따르면 NTK는 수학적으로는 다음과 같이 표현한다. 어떤 parameter $\theta$에 의존하는 함수 $f$ (추후에 모델이 되는 함수)에 대해서, 초기 파라미터 $\theta_0$ 기준으로 $f$를 $\theta$과 입력값 $x$ 대해 다음과 같이 확장할 수 있다. 이 때, $\langle , \rangle$은 내적이며, 우변은 선형 모델(linear model)처럼 작동한다.

\[\begin{align} f(x; \theta) - f(x; \theta_0) \approx \langle \nabla_\theta f(x; \theta_0), \theta - \theta_0 \rangle \end{align}\]

위에서 언급했듯이 우변은 선형 모델처럼 작동한다. 위 식을 선형 모델의 형태로 다시 작성하면 다음과 같다. 이는 어떻게보면 $(fx; \theta)$의 $w$에 대한 1st order taylor expansion이라고 볼 수 있다.

\[\begin{align} f(x; \theta) \approx f(x; \theta_0) + \nabla_\theta f(x; \theta_0)^\mathsf{T} (\theta - \theta_0) \end{align}\]

위 식에서 $f(x; \theta_0)$는 초기값, \(\nabla_\theta f(x; \theta_0)\)는 $\theta_0$에 의존하므로 상수라고 생각할 수 있고, $\theta - \theta_0$는 정확히는 변수 $\theta$에 대한 선형 모델로 볼 수 있다. 하지만, 모델 함수 gradient를 찾는것은 선형(linear)이지 않기에 모델 함수는 비선형(nonlinear)이라고 생각할 수 있다.

그러나 NTK는 \(\nabla_\theta f(x; \theta_0)\)를 input featurizer 혹은 feature map이라고 불리우는 nonlinear 함수라고 증명한다.

물론 이 가정은 $\theta$와 $\theta_0$의 차이가 크지 않을 때만 잘 작동한다. 신경망(neural network)에서는 작은 learning rate로 매우 적은 시간에 훈련했을 때만 성립할 수 있다.

width가 클 수록 즉 무한 너비(infinite-width) 네트워크에서 $\theta_0$이 랜덤하게 잘 초기화되었다면, weight들이 변화량($\theta - \theta_0$에 대한 기대값이 거의 0에 가깝다. 여기에 대한 직관적인 설명은 width가 클 수록 모델의 output에 영향을 주는 weight들이 많아지기 떄문에, $\theta$의 작은 변화라도 $f$에는 영향이 클 수 있다는 점이다. 따라서 weight가 굉장히 조금만 움직이게 되고 이는 모델이 lienar하게 작동할 수 있게 된다.

내가 느끼기엔 이 가정은 수치해석에서의 Euler Method의 가정과 별로 차이가 없어보인다. Unstable하지만 않는다면 복잡한 식이어도 매우 작은 time step을 가정한다면 (비효율적이지만) linear하게 근사해서 풀 수 있기 때문이다.

NTK 논문 (Jacot, Gabriel, and Hongler 2018)은 이 직관을 infinite width 모델이기만 하면 어떤 데이터든간에 적용할 수 있음을 보였다. 이를 통해, 비선형 모델도 선형처럼 해석이 가능해지고, 이는 training dynamics를 해석할 수 있게 만들어준다.

NTK: Gradient Flow

NTK논문은 gradient flow라는 것을 제시하여 gradient descent에서의 training dynamics를 해석하고자 한다.

모델 weight $\theta$가 업데이트되는 과정을 다음과 같이 나타내면, 이를 learning rate $\eta$를 일종의 time처럼 생각하는 1D ODE로 표현할 수 있게 되고, ODE의 해를 구하면 언제나 해가 존재할 수 있음을 증명했다. 우선 $L$을 $f$에 대한 loss function라고 하자.

\[\begin{align} \theta_{k+1} &= \theta_k - \eta \nabla_\theta L(\theta_k) \\ \dfrac{\theta_{k+1} - \theta_k}{\eta} &= -\nabla_\theta L(\theta_k) \\ \dfrac{d \theta(t)}{dt} &= -\nabla_\theta L(\theta (t)) \\ \end{align}\]

마지막 식은 1D ODE 가장 기본적인 형태 그 자체라고 할 수 있다. 하지만, 그 주체가 $\theta$일 뿐. 그래서 Gradient Flow라고 이름붙였다고 생각한다.

여기서 loss function $\mathcal{L}$을 MSE function이라고 가정하고, $f^*$를 정답 레이블이라고 하자. Loss function을 풀어써서 미분을 적용하면 다음과 같다.

\[\begin{align} \dfrac{d \theta(t)}{dt} &= -\nabla_\theta \mathcal{L}(\theta (t)) \\ \dot{\theta}(t) &= -\nabla_\theta (f(\theta) - f^*)^2\\ \dot{\theta} &= -(\nabla_\theta f(\theta)) (f(\theta) - f^*) \end{align}\]

이를 $f$에 적용하기 위해 Chain rule를 적용한다.

\[\begin{align} \dot{f}(\theta) &= \dfrac{d f(\theta(t))}{d \theta(t)} \dfrac{d \theta(t)}{dt} = \nabla_\theta f(\theta)^\mathsf{T} \dot{\theta} \\ \dot{f}(\theta) &= \nabla_\theta f(\theta)^\mathsf{T} \dot{\theta} = -\nabla_\theta f(\theta)^\mathsf{T} \nabla_\theta f(\theta) (f(\theta) - f^*) \\ \end{align}\]

여기서 나온 \(\nabla_\theta f(\theta)^\mathsf{T} \nabla_\theta\)를 NTK(Neural Tangent Kernel)이라고 정의한다.

좀 더 자세한 내용은 원 논문과 (Jacot, Gabriel, and Hongler 2018) 이 블로그에 정리가 잘 되어있다. 개인적으로는 논문은 어려워서 이해가 잘 안됐지만, 해당 블로그가 정말 쉽게 잘 설명되어 있어서 읽기 좋았다.

NTK: NTK INIT

위의 (Yang 2020)의 표현으로 다시 바꾸고 정리하면 다음과 같다. $f(x; \theta)$를 파라미터 $\theta$와 input $x$에 대한 신경망이라고 할 때, $\mathcal{L}$을 Loss, $y$를 label라고 하자. 서로 다른 input $x$와 $\bar{x}$에 대해서 NTK $\Theta$를 다음과 같이 정의할 수 있다.

\[\begin{align} f_t - f_{t-1} &\approx -\eta \mathcal{\Theta} \mathcal{L}' (f_t, y) \\ \Theta (x, \bar{x}) &\stackrel{\text{def}}{=} \langle \nabla_\theta f(x; \theta_0), \nabla_\theta f(\bar{x}; \theta_0) \rangle \end{align}\]

또한 (Jacot, Gabriel, and Hongler 2018)에서 보여줬듯이 $\theta$가 랜덤하게 잘 intialized되었고, $f$의 width가 충분히 크다면 (infinite-width), $\Theta$는 deterministic한 $\mathring{\Theta}$로 수렴한다.

이를 수학적으로 표현하면, $L$개의 hidden layer를 가지며, layer $l$의 width를 $n^l$이라고 할 때, NTK $\Theta (x, \bar{x})$는 $\theta$가 랜덤이어도 deterministic한 kernel $\mathring{\Theta} (x, \bar{x})$으로 수렴한다.

\[\begin{align} \Theta \stackrel{p}{\rightarrow} \mathring{\Theta} \textrm{ as } n^1, \dots, n^L \rightarrow \infty \textrm{ in that sequence} \end{align}\]

NTK: NTK TRAIN

수렴 여부뿐만 아니라 이 MLP $f$의 훈련과정을 생각해보자. Loss function $\mathcal{L}$을 사용하여 gradient descent로 train하는 하는 시간을 $t$라고 정의하자. 처음 가우시안 랜덤변수로 초기화한 MLP를 $f_0$, 시간에 따른 MLP를 $f_t$라고 했을 때, 어떤 고정된 시간 $T$에 대해서 width가 충분히 크다면 MLP 모델은 $\mathring{f}$로 수렴한다.

\[\begin{align} f_t &\rightarrow \mathring{f}_t \textrm{ for all } t < T, \textrm{ where } f_0 \rightarrow \mathring{f}_0 \\ \partial_t \mathring{f}_t &= -\eta \mathring{\Theta} \cdot \nabla_f \mathcal{L}(\mathring{f}_t) \end{align}\]

위에서도 유도했듯이 위 식은 true label $f^*$에 대해 1D ODE로 변환될 수 있다.

\[\begin{align} \mathring{f}_t - f^* = e^{-\eta t \mathring{\Theta}} (f_0 - f^*) \end{align}\]

NTK Decomposition

MLP용 NTK를 다른 모델(RNN, transformer 등)에 확장하기 위해서는 기존 MLP 표현법에 조금 변화가 필요하다. 왜냐하면, (Jacot, Gabriel, and Hongler 2018) 원 논문의 방법으로는 MLP가 귀납적(inductive)으로 표현되어 있어서 확장하기가 어렵기 때문이다. 이렇게 변형된 표현의 의미를 이해하는 것이 (Yang 2020)의 핵심적인 내용이다.

원래의 방식을 NTK parameterization이라고 하는데 다음과 같이 정의한다.

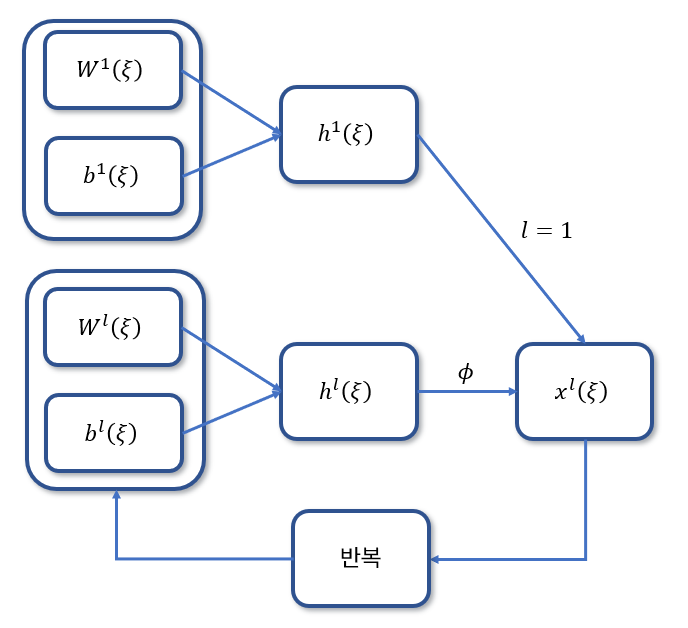
input $\xi \in \mathbb{R}^{n^0}$, output dimension $n^{L+1}=1$이라고 할 떄, MLP를 $f(\xi; \theta) = W^{L+1} x^L(\xi)$라고 표현하면, $l=2, \dots, L$에 대해서 재귀적으로 다음과 같이 정의할 수 있다.

\[\begin{align} h^l(\xi) &= W^l x^{l-1}(\xi) + b^l \in \mathbb{R}^{n^l} \\ x^l(\xi) &= \phi(h^l(\xi)) \\ h^1(\xi) &= W^1 \xi + b^1 \in \mathbb{R}^{n^1} \end{align}\]

NTK Parameterization

MLP Parameter는 \(\theta = \{ w^l \in \mathbb{R}^{n^l \times n^{l-1}}\}_{l=1}^{L+1} \cup \{ b^l \in \mathbb{R}^{n^l }\}_{l=1}^{L}\)로 정의되고, $W^l$은 $w^l$을 \(\sqrt{n^{l-1}}\)로 나눠준 값으로 정의한다. \(W^l= \dfrac{1}{\sqrt{n^{l-1}}} w^l\) 여기서 $\phi$는 activation function이다. 이는 (Poole et al. 2016)로부터 내려오는 유구한 notation이다.

이제 NTK parameterization을 NTK의 정의에 결합시킨다.

\[\begin{align} \Theta (\xi, \bar{\xi}) &= \langle \nabla_\theta f(\xi; \theta_0), \nabla_\theta f(\bar{\xi}; \theta_0) \rangle \\ &= \sum_{l=1}^{L+1} \langle \nabla_{w^{l}} f(\xi),\nabla_{w^{l}} f(\bar{\xi}) \rangle + \sum_{l=1}^L \langle \nabla_{b^{l}} f(\xi),\nabla_{b^{l}} f(\bar{\xi}) \rangle \end{align}\]

\(W^l= \dfrac{1}{\sqrt{n^{l-1}}} w^l\)와 chain rule을 고려하면, $\nabla_{w^{l}} f(\xi)$는 다음과 같이 두 matrix의 곱으로 표현할 수 있으며 이는 $n^l \times 1 $와 $1 \times n^{l-1}$의 곱인 $ n^l \times n^{l-1}$ matrix이다.

\[\begin{align} \nabla_{w^{l}} f(\xi) = \left( \dfrac{1}{\sqrt{n^{l-1}}} \nabla_{h^l} f(\xi) \right) \left( x^{l-1}(\xi)^\mathsf{T} \right) \end{align}\]

편의를 위해 논문에 나온 abbreviation($\bullet = \bullet (\xi)$,$\bar{\bullet} = \bullet (\bar{\xi})$)을 사용하고, \(dh^l = \sqrt{n^{l}} \nabla_{h^{l}} f(\xi)\)와 \(d\bar{h}^l = \sqrt{n^{l}} \nabla_{h^{l}} f(\bar{\xi})\)이라는 것을 정의하면,

\[\begin{align*} \nabla_{w^{l}} f(\xi) &= \dfrac{1}{\sqrt{n^{l-1}}} \nabla_{h^l} f(\xi) x^{l-1}(\xi)^\mathsf{T} \\ &= \dfrac{1}{\sqrt{n^{l-1}} \sqrt{n^{l}}} \sqrt{n^{l}} \nabla_{h^l} f(\xi) x^{l-1}(\xi)^\mathsf{T} \\ &= \dfrac{1}{\sqrt{n^{l} n^{l-1}}} dh^l x^{l-1}(\xi)^\mathsf{T} \end{align*}\] \[\begin{align*} \nabla_{w^{l}} f(\bar{\xi}) &= \dfrac{1}{\sqrt{n^{l-1}}} \nabla_{h^l} f(\bar{\xi}) x^{l-1}(\bar{\xi})^\mathsf{T} \\ &= \dfrac{1}{\sqrt{n^{l-1}} \sqrt{n^{l}}} \sqrt{n^{l}} \nabla_{h^l} f(\bar{\xi}) x^{l-1}(\bar{\xi})^\mathsf{T} \\ &= \dfrac{1}{\sqrt{n^{l} n^{l-1}}} d\bar{h}^l x^{l-1}(\bar{\xi})^\mathsf{T} \end{align*}\]

자 이제 원래 내적(inner product)에 넣어서 계산해보자. 내적을 trace inner product로 표현하고, cyclic property of trace inner product ($Tr(ABC) = Tr(BCA) = Tr(CBA)$)를 사용하면 다음과 같다.

\[\begin{align*} \langle \nabla_{w^{l}} f(\xi),\nabla_{w^{l}} f(\bar{\xi}) \rangle &= \dfrac{1}{n^{l} n^{l-1}} \langle dh^l x^{l-1 \mathsf{T}}, d\bar{h}^l \bar{x}^{l-1 \mathsf{T}} \rangle \\ &=\dfrac{1}{n^{l} n^{l-1}} Tr\left( \left(dh^l x^{l-1 \mathsf{T}} \right)^\mathsf{T} d\bar{h}^l \bar{x}^{l-1 \mathsf{T}} \right) \\ &=\dfrac{1}{n^{l} n^{l-1}} Tr\left( x^{l-1} dh^{l \mathsf{T}} d\bar{h}^l \bar{x}^{l-1 \mathsf{T}} \right) \\ &=\dfrac{1}{n^{l} n^{l-1}} Tr\left( x^{l-1} \left(dh^{l \mathsf{T}} d\bar{h}^l \right) \bar{x}^{l-1 \mathsf{T}} \right) \\ &=\dfrac{1}{n^{l} n^{l-1}} Tr\left( \left(dh^{l \mathsf{T}} d\bar{h}^l \right) \bar{x}^{l-1 \mathsf{T}} x^{l-1} \right) \\ &=\left(\dfrac{dh^{l \mathsf{T}} d\bar{h}^l}{n^{l}} \right) \left( \dfrac{\bar{x}^{l-1 \mathsf{T}} x^{l-1}}{n^{l-1}} \right)\\ &=\left(\dfrac{dh^{l \mathsf{T}} d\bar{h}^l}{n^{l}} \right) \left( \dfrac{x^{l-1 \mathsf{T}} \bar{x}^{l-1}}{n^{l-1}} \right)\\ \end{align*}\]

마지막에 $Tr$이 사라지는 것은 $dh^{l \mathsf{T}} \in \mathbb{R}^{1\times n^l}, d\bar{h}^l \in \mathbb{R}^{n^l \times 1}$이고, $\bar{x}^{l-1 \mathsf{T}} \in \mathbb{R}^{1\times n^{l-1}}, x^{l-1} \in \mathbb{R}^{n^{l-1} \times 1}$이라서 각각 scalar 값이 나오기 때문이다. 그러기에 맨 마지막 식에서 \(\bar{x}^{l-1 \mathsf{T}} x^{l-1}\)이 \(x^{l-1 \mathsf{T}} \bar{x}^{l-1}\)로 변환될 수 있다.

결론적으로 NTK를 두 입력 $\xi, \bar{\xi}$에 대해 decompose하면 \(x^{l-1 \mathsf{T}} \bar{x}^{l-1}\)와 \(dh^{l \mathsf{T}} d\bar{h}^{l \mathsf{T}} / n^l\)의 곱으로 표현할 수 있고, 이는 각각 forward와 backward quantity라고 간주할 수 있다. 다음 두 섹션은 각 quantity가 어떤 값으로 수렴하는지에 대한 논의를 진행하고자 한다.

Limits of Forward Quantities $x^{l \mathsf{T}} \bar{x}^{l} / n^l$

기존에 (Poole et al. 2016), (Schoenholz et al. 2016)에서 딥러닝을 mean-field theory로 설명하고자 했다. 이 논문들에서 나온 아이디어를 바탕으로 $\bar{x}^{l \mathsf{T}} x^{l}$를 분석할 수 있다.

평균장 이론(mean field theory)은 원래 통계물리학에서 각 개별입자가 전체 시스템의 평균적 효과에 의해 영향을 받는다고 가정하여 계의 거동을 설명하는 이론이다. 물리학에서의 복잡계를 딥러닝이라고 간주하면, 각 뉴런을 입자에 대응시킬 수 있고, 입자의 상호작용을 평균적인 필드에 대해서 설명하는 mean field theory를 딥러닝에 적용할 수 있게 된다. 유체역학에서 control volume을 사용하는것과 아이디어는 비슷하다고 생각된다. 자세한 내용은 다음 영상을 확인하면 좋다.

여기서 중요한 것은 mean field theory를 적용할때는 각 요소는 독립적으로 행동한다고 가정하기 때문에, weight와 bias는 각각 가우시안 분포를 따른다고 가정한다.

자 이 이론을 가지고 \(\dfrac{x^{l \mathsf{T}} \bar{x}^{l}}{n}\)이 다음과 같이 deterministic한 scalar \(C^l(\xi, \bar{\xi})\)로 수렴한다는 것을 보이고자 한다.

\[\begin{align} \dfrac{x^{l \mathsf{T}} \bar{x}^{l}}{n} \rightarrow C^l(\xi, \bar{\xi}) \end{align}\]

\(\dfrac{x^{l \mathsf{T}} \bar{x}^l}{n}\)는 두 벡터 \(x^l\)와 \(\bar{x}^l\)의 내적의 평균이다. 또한 \((x^l_\alpha, \bar{x}^l_\alpha)\)는 직관적으로 roughly i.i.d.라고 가정할 수 있다. 이렇게 되는 이유는 weight와 bias는 guassian이지만 지속적으로 weight와 bias가 곱해지고 더해지기 때문에 레이어가 지날 수록 다른 input \(\xi, \bar{\xi}\)에 대해서 correlated되었다고 생각할 수 있기 때문이다.

공교롭게도, Covariance의 기본적인 정의는 다음과 같다. 여기서 쓰이는 \(\bar{x}, \bar{y}\)는 확률 변수 \(X\)와 \(Y\)의 평균을 뜻한다.

\[\begin{align} Cov(X, Y) \approx \dfrac{1}{n} \sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y}) \end{align}\]

그리고 확률 변수 \(X\)와 \(Y\)가 Gaussian 분포라면 평균은 0이기 때문에 위 식은 다음과 같이 변한다.

\[\begin{align} \mathrm{Cov}(X, Y) \approx \dfrac{1}{n} \sum_{i=1}^n x_i y_i \end{align}\]

그리고 두 벡터 \(\mathbf{x}, \mathbf{y}\)의 내적의 평균은 일반식으로 다음과 같이 표현된다.

\[\begin{align} \dfrac{1}{n} \mathbf{x} \cdot \mathbf{y} = \dfrac{1}{n} \sum_{i=1}^n x_i y_i \end{align}\]

동일하지 않은가! 즉, \(\dfrac{x^{l \mathsf{T}} \bar{x}^l}{n}\)는 결국 공분산(Covariance)를 구하는 문제로 환원될 수 있다.

이를 확인하기 위해 레이어 $l$의 요소 \(\alpha \in [n^l]\)를 기준으로 MLP Layer를 풀어써보고자 한다. $\alpha$에 대해서 좌표 $(W^l x^{l-1})$는 다음과 같이 표현할 수 있다.

\[\begin{align} (W^l x^{l-1})_\alpha = \sum_{\beta=1}^n W_{\alpha \beta}^l x_\beta^{l-1} \end{align}\]

이는 \(h^l(\xi) = W^l x^{l-1}(\xi) + b^l\)을 각 원소 좌표 $\alpha, \beta$에 대해 풀어쓴거라고 볼 수 있다. \(W_{\alpha \beta}^l x_\beta^{l-1}\)는 roughly i.i.d. random variable 이다. 처음 레이어에서는 완벽하게 i.i.d.를 맞춰서 샘플링하더라도 훈련이 진행되면서 weight의 분포가 달라지거나 레이어 간의 상관관계가 생겨서 i.i.d.가정이 깨지기 때문이다. 하지만 i.i.d.처럼 취급한다. 그런 이유로 Gaussian distribution을 따르는 roughly i.i.d. 랜덤변수의 평균은 0이고, \(W_{\alpha \beta}^l x_\beta^{l-1}\)의 분산은 다음과 같이 구할 수 있다. ($Var(X)=E(X^2) - [E(X)]^2$)

\[\begin{align*} \mathbb{E}(W^l x^{l-1})^2_\alpha &= \mathbb{E}((W^l x^{l-1})^2_\alpha)\\ &= \mathbb{E}\left(\left(\sum_{\beta=1}^n W_{\alpha \beta}^l x_\beta^{l-1}\right)^2\right) \\ &= \mathbb{E}\left(\left(W_{\alpha 1}x_1 + W_{\alpha 2}x_2 + \cdots + W_{\alpha n}x_n\right)^2\right) \\ &= \mathbb{E}(W_{\alpha 1}^2 x_1^2 + W_{\alpha 2}^2 x_2^2 + \cdots + W_{\alpha n}^2 x_n^2 + 2 W_1 x_1 W_2 x_2 ) \\ &= \mathbb{E}(W_{\alpha 1}^2 x_1^2 + W_{\alpha 2}^2 x_2^2 + \cdots + W_{\alpha n}^2 x_n^2 ) \\ &= \mathbb{E}(W_{\alpha 1}^2 x_1^2) + \mathbb{E}(W_{\alpha 2}^2 x_2^2) + \cdots + \mathbb{E}(W_{\alpha n}^2 x_n^2 ) \\ &= \mathbb{E}(W_{\alpha 1}^2) \mathbb{E}(x_1^2) + \mathbb{E}(W_{\alpha 2}^2) \mathbb{E}(x_2^2) + \cdots + \mathbb{E}(W_{\alpha n}^2) \mathbb{E}(x_n^2 ) \\ &= \sum_{\beta=1}^n \mathbb{E}((W_{\alpha \beta}^l)^2) \mathbb{E}((x_{\beta}^{l-1})^2) \\ &= \lVert x \rVert^2 / n^{l-1} \\ &\approx C^{l-1} (\xi, \xi) \end{align*}\]

위 식에 필요한 정보는 roughly i.i.d. 특성에 의해 \(\mathbb{E}(2 W_1 x_1 W_2 x_2 ) = 2 \mathbb{E}(W_1) \mathbb{E}(x_1) \mathbb{E}(W_2) \mathbb{E}(x_2) = 0\)이 된다는 점과, NTK의 Lecun initialization에 의해 \(W_{\alpha \beta}^l \sim \mathcal{N} \left(0, \dfrac{1}{n^l}\right)\) 라는 점이다. 여기서 $C$는 어떤 deterinstic한 scalar값이다.

위의 분산과 Central Limit Theorem을 적용하면 \((W^l x^{l-1})_\alpha \sim \mathcal{N} (0, C^{l-1} (\xi, \xi))\)이 되며 마찬가지로 $\bar{x}$에 대해서도 \((W^l \bar{x}^{l-1})_\alpha \sim \mathcal{N} (0, C^{l-1} (\bar{\xi}, \bar{\xi}) )\) 로 나타낼 수 있다. 두 랜덤 변수 \(((W^l x^{l-1})_\alpha, (W^l \bar{x}^{l-1})_\alpha )\), 즉 \((x^{l-1}_\alpha, \bar{x}^{l-1}_\alpha)\)는 jointly Gaussian이며 이들의 covariance는 \(C^{l-1} (\xi, \bar{\xi})\) 이다.

\(x^{l} (\xi) = \phi (h^l (\xi))\) 이고, \(h\)는 이미 선형 변환(linear transform)이라는 점을 알고 있고, \(phi\)는 activation function에 의한 비선형 변환(nonlinear transform)이라는 것을 알 수 있다. roughly i.i.d. 특성 덕분에 \((x^l_\alpha, \bar{x}^l_\alpha)\)는 \((\phi(\xi), \phi(\bar{\xi}))\)와 같은 분포라고 이야기할 수 있다. 그러면 \(\mathbb{E}(\phi(\xi))=0, \mathbb{E}(\phi(\bar{\xi}))=0\) 특성과 결합하면 Covariance는 다음과 같이 표현이 가능하다.

\[\begin{align} \mathrm{Cov}(x^l_\alpha, \bar{x}^l_\alpha) &= \mathrm{Cov}(\phi(\xi), \phi(\bar{\xi}) \\ &= \mathbb{E}(\phi(\xi), \phi(\bar{\xi}) - \mathbb{E}(\phi(\xi))\mathbb{E}(\phi(\bar{\xi}) \\ &= \mathbb{E}(\phi(\xi), \phi(\bar{\xi}) \end{align}\]

Lecun initialization에 의해 bias는 $b \sim \mathcal{N} (0, 1)$이라고 정의되며, 이를 종합하면 이 전 layer의 scalar \(C^{l-1}\)에 의존하는 (Yang 2020)의 Eq. (6)이 나오게 된다.

\[\begin{align} C^{l} (\xi, \bar{\xi}) = \mathbb{E} (\phi(\xi) \phi(\bar{\xi})), \textrm{ where } \\ (\xi, \bar{\xi}) \sim \mathcal{N} \left(0, \begin{pmatrix} C^{l-1} (\xi, \xi) & C^{l-1} (\xi, \bar{\xi}) \\ C^{l-1} (\xi, \bar{\xi}) & C^{l-1} (\bar{\xi}, \bar{\xi}) \end{pmatrix} + 1 \right) \end{align}\]

Limits of Backward Quantities $dh^{l \mathsf{T}} d\bar{h}^{l} / n^l$

우선 각 layer의 크기가 다르면 복잡하므로 \(n^1 = \cdots = n^L\)이라고 가정한 뒤 시작한다. 그리고 \(dh^l = \sqrt{n^{l}} \nabla_{h^{l}} f(\xi)\)을 정의했던 것처럼 \(dx^l_\alpha\)를 \((W^{l+1 \mathsf{T}}dh^{l+1})_\alpha\)이라고 정의한다. 이는 레이어 $l+1$에서 $l$로 전파되는 gradient이다.

1. Backpropagation을 돌이켜보면 forward propagation은 다음과 같이 전파된다. \(\begin{align*} h^l (\xi) = W^l x^{l-1} (\xi) + b^l \end{align*}\)
2. 각 레이어의 결과 $h^l$은 activation function $\phi$를 통해 최종 출력 $x^l$로 변환된다. \(\begin{align*} x^l = \phi(h^l) \end{align*}\)
3. 최종 출력 레이어에서 loss function $\mathcal{L}$에 대한 출력 값의 gradient를 계산한다. \(\begin{align*} \nabla_{x^L} \mathcal{L} \end{align*}\)
4. 여기서 나온 $\nabla_{x^L} \mathcal{L}$의 backpropagation 과정의 첫번째 gradient이다. 각 레이어 l에 대해 activation function의 미분 $\phi’$를 적용해서 기울기를 구한다. 이 때 $\odot$은 Hadamard product를 의미한다. \(\begin{align*} \nabla_{h^l} \mathcal{L} = \nabla_{x^l} \mathcal{L} \odot \phi'(h^l) \end{align*}\)
5. MLP 레이어의 weight와 bias에 대해 loss에 대한 gradient를 계산한다. 이 때 bias는 batch 전체의 weight를 더해주어야 한다. \(\begin{align*} \nabla_{W^l} \mathcal{L} = \nabla_{h^l} \mathcal{L} \cdot (x^{l-1})^{\mathsf{T}}, \nabla_{b^l} \mathcal{L} &= \sum \nabla_{h^l} \mathcal{L} \end{align*}\)
6. 현재 레이어 $l$의 weight $W$의 trace를 사용하여 이전 레이어 $l-1$의 출력에 대한 gradient를 계산한다. \(\begin{align*} \nabla_{x^{l-1} \mathcal{L}} = (W^l)^{\mathsf{T}} \nabla_{h^l} \mathcal{L} \end{align*}\)

이 과정을 새로운 \(d x^l_\alpha\)의 정의와 결합하면 다음과 같다. 위에서 사용한 $\nabla$대신 $d$를 써준다고 생각하면 이해하기 쉽다.

\[\begin{align} d x^l_\alpha &\stackrel{\text{def}}{=} (W^{l+1 \mathsf{T}}dh^{l+1})_\alpha \\ &= (W^{l+1 \mathsf{T}} (dx^{l+1} \odot \phi'(h^{l+1})))_\alpha \\ &= \sum_\beta W^{l+1}_{\beta \alpha} dx^{l+1}_{\beta} \phi' (h^{l+1}_\beta) \end{align}\]

전부가 i.i.d.라서 central limit theorem을 사용하면 좋겠지만, \(h^{l+1}_\beta\)는 모든 $\gamma$에 대해 \(W^{l+1}_{\beta \gamma}\)에 의존하기 때문에 i.i.d. 를 만족하지 못한다. 그러나, (Poole et al. 2016)와 (missing reference)에 따르면, 이 의존성은 무시해도 된다고 한다. 이는 mean field theory에서 뉴런의 크기 $n^l$이 크다면, weight와 bias는 독립적으로 작용하여 이전 레이어의 영향을 받지 않고 $h$는 이런 $W$와 $b$의 weighted sum이라고 표현할 수 있기 때문이다.

이를 통해 (Yang 2020)에서는 다음과 같은 아주 재미있는 Heuristic을 사용하게 된다. (Schoenholz et al. 2016)의 Section 4와 (Yang and Schoenholz 2017)의 Axiom 3.2를 참고하면 되겠다. Forward와 Backward pass의 weight가 서로 독립적이라니 이 얼마나 재밌는 가정이지 않은가!

Heuristic 4.1 (gradient independent assumption, or GIA), For any matrix \(W\), we assume \(W^{\mathsf{T}}\) used in backprop is independent from \(W\) used in forward pass.

여튼, 위 가정과 함께 Limits of Forward Quantities \(\bar{x}^{l-1 \mathsf{T}} x^{l-1}\)에서 했던 방식을 똑같이 적용할 수 있다. Backward pass의 weight는 forward pass때의 weight와 독립적이니 동일한 방식을 의심없이 적용할 수 있게 되었다. 그러면 $x$대신에 $dh$로 기호를 바꾼셈이 되어버려서 \(d x^{l}_\alpha\)는 \(\mathcal{N}(0, \lVert d h^{l+1} \rVert^2 / n^{l+1})\) 분포를 따르며 \(\alpha\)에 대해 roughly i.i.d.를 만족한다고 할 수 있다. 또한 pair \((dx^l_\alpha, d \bar{x}^l_\alpha) \stackrel{\text{def}}{=} ((W^{l+1 \mathsf{T}}dh^{l+1})_\alpha, (W^{l+1 \mathsf{T}}d \bar{h}^{l+1})_\alpha)\) 역시 zero mean과 \(\lVert d h^{l+1} d \bar{h}^{l+1} \rVert^2 / n^{l+1}\)를 만족하는 \(\alpha\)에 대한 i.i.d.분포라고 할 수 있다. (jointly Gaussian) \(dx^l_\alpha\)뿐만 아니라 \(h\)로 확장하면 \((h^{l}, \bar{h}^{l})\) 역시 roughly i.i.d이기 때문에 \((dh^{l}_\alpha, \bar{h}^{l}_\alpha) = (d x_\alpha^{l} \phi'(h^l_\alpha), d \bar{x}_\alpha^{l} \phi'(\bar{h}^l_\alpha) )\) 도 비슷한 결과를 가진다고 얘기할 수 있다.

이로써 Backward quantities $dh^{l \mathsf{T}} d\bar{h}^{l} / n^l$에 도달하였다. 이전 섹션에서의 $C$대신 Scalar $D^l (\xi, \bar{\xi})$를 도입하여 variance를 표현하면 다음과 같은 backward quantities의 covariance는 $D$로 수렴한다.

\[\begin{align} \dfrac{dh^{l \mathsf{T}} d\bar{h}^{l}}{n^l} \rightarrow D^l (\xi, \bar{\xi}) \end{align}\]

그리고 $D^l (\xi, \bar{\xi})$ 도 다음과 같은 재귀함수로 정의된다.

\[\begin{align} D^l (\xi, \bar{\xi}) &= \mathbb{E}_{\eta \bar{\eta}} \mathbb{E} \phi'(\xi) \phi'(\bar{\xi}) = D^{l+1} (\xi, \bar{\xi}) \mathbb{E} \phi'(\xi) \phi'(\bar{\xi}) \\ \textrm{ where } (\eta, \bar{\eta}) &\sim \mathcal{N} \left(0, \begin{pmatrix} D^{l+1} (\xi, \xi) & D^{l+1} (\xi, \bar{\xi}) \\ D^{l+1} (\xi, \bar{\xi}) & D^{l+1} (\bar{\xi}, \bar{\xi}) \end{pmatrix}\right) \\ (\xi, \bar{\xi}) &\sim \mathcal{N} \left(0, \begin{pmatrix} C^{l} (\xi, \xi) & C^{l} (\xi, \bar{\xi}) \\ C^{l} (\xi, \bar{\xi}) & C^{l} (\bar{\xi}, \bar{\xi}) \end{pmatrix} + 1 \right) \end{align}\]

Foward Quantities $x^{l \mathsf{T}} \bar{x}^{l} / n^l$ + Backward Quantities $dh^{l \mathsf{T}} d\bar{h}^{l} / n^l$

이전에 NTK Decomposition을 사용하여 다음과 같이 유도하였다.

\[\begin{align*} \langle \nabla_{w^{l}} f(\xi),\nabla_{w^{l}} f(\bar{\xi}) \rangle = \left(\dfrac{dh^{l \mathsf{T}} d\bar{h}^l}{n^{l}} \right) \left( \dfrac{\bar{x}^{l-1 \mathsf{T}} x^{l-1}}{n^{l-1}} \right) \end{align*}\]

지금까지 각 항에 대해 정의한 $C$와 $D$에 대해 표현하면 다음과 같다.

\[\begin{align*} \langle \nabla_{w^{l}} f(\xi),\nabla_{w^{l}} f(\bar{\xi}) \rangle = C^{l-1} (\xi, \bar{\xi}) D^{l} (\xi, \bar{\xi}), \forall l \in [2, L] \end{align*}\]

마찬가지로, bias에 대해서도 $\nabla_{b^l} f(\xi) = \nabla_{h^l} f(\xi) = dh^l / \sqrt{n^l}$이므로,

\[\begin{align*} \langle \nabla_{b^{l}} f(\xi),\nabla_{b^{l}} f(\bar{\xi}) \rangle = D^{l} (\xi, \bar{\xi}), \forall l \in [2, L] \end{align*}\]

기존 NTK 정의와 결합하면 \(\begin{align} \Theta (\xi, \bar{\xi}) &= \langle \nabla_\theta f(\xi; \theta_0), \nabla_\theta f(\bar{\xi}; \theta_0) \rangle \\ &= \sum_{l=1}^{L+1} \langle \nabla_{w^{l}} f(\xi),\nabla_{w^{l}} f(\bar{\xi}) \rangle + \sum_{l=1}^L \langle \nabla_{b^{l}} f(\xi),\nabla_{b^{l}} f(\bar{\xi}) \rangle \\ &= \sum_{l=1}^{L+1} C^{l-1} (\xi, \bar{\xi}) D^{l} (\xi, \bar{\xi}) + \sum_{l=1}^L D^{l} (\xi, \bar{\xi}) \\ \end{align}\)

이를 통해 MLP에 대해서 기존 NTK보다 훨씬 심플하게 $C$와 $D$라는 Scalar의 곱으로 표현하였다. 이 논문의 키 포인트는 NTK로부터 해당 식을 유도하고, 이를 다른 아키텍처 즉 CNN이나 RNN으로 확장하고자 하는 것이다.

NTK -> Any Architecture

(Yang 2020)은 지금까지의 과정이 과연 generalized될 수 있는가에 대해 독자들이 생각할 수 있는 질문에 대한 답을 미리 준비해 놓았다. 지금까지의 과정은 MLP였기 때문에 가능한 것이 아닌가라는 의심은 당연한 것이기 때문이다.

NTK Decomposition을 의미있게 일반화할 수 있는가?

다음 분해는 MLP라는 가정하에서 이루어졌다. 그러나 \(\frac{dh^{l \mathsf{T}} d\bar{h}^l}{n^l}\)같은 값들이 수렴할지 어떻게 알 수 있으며, 발산하지 않는다는 보장이 어디 있는가? \(\begin{align} \Theta (\xi, \bar{\xi}) &= \langle \nabla_\theta f(\xi; \theta_0), \nabla_\theta f(\bar{\xi}; \theta_0) \rangle \\ &= \sum_{l=1}^{L+1} \langle \nabla_{w^{l}} f(\xi),\nabla_{w^{l}} f(\bar{\xi}) \rangle + \sum_{l=1}^L \langle \nabla_{b^{l}} f(\xi),\nabla_{b^{l}} f(\bar{\xi}) \rangle \\ \end{align}\)

이에 대해 저자는 NTK를 NTK Decomposition, 즉 inner product의 곱셈의 합으로 분해할 수 있도록 일반화할 수 있다고 생각한다. NTK가 수렴한다면 말이다. 이는 다음 섹션 Strategy for Computing the Infinite-Width NTK에서 어떻게 일반화할지 보여줄 예정이다.

GIA를 계속 가정해도 되는가?

아까도 재밌다고 언급했는데, forward pass와 backward pass의 gradient가 서로 독립적이라는 가정이 과연 지속적으로 유효한 가정인가에 대한 의문은 있을 수 있다.

이에 대한 저자는 다음 조건하에서 GIA를 만족한다고 한다.

Conditon 1 (Simple GIA Check) The output layer (like \(W^{L+1}\) in the MLP above) is sampled independently and with zero mean from all other parameters and is not used anywhere else in the interior of the network

이는 Backpropgation의 경우 output layer를 통해 forward pass와 backward pass가 상호작용할 수 있기 때문이다. 자세한 것은 Strategy for Computing the Infinite-Width NTK에서 다룰 예정이다.

현대의 복잡한 신경망에 대해 적용할 수 있는가?

CNN, RNN, LSTM 등 뿐만 아니라 ResNet, transformer에도 NTK Decompositon을 적용할 수 있는가에 대해서 당연히 의문이 들 수 밖에 없다.

저자 말로는 저자가 만든 NETSOR\(\mathsf{T}\) 언어 (NETSOR의 확장판)로 표현할 수 있는 네트워크는 적용할 수 있다고 한다. NETSOR을 처음 봤을 때는 이걸 굳이 따로 만들어야 하는 이유가 있나라는 의문이 있었는데, 이제 조금 납득이 간다. 하지만, 이미 포스트가 너무 길기 때문에 NETSOR은 다른 포스트에서 다룰 예정이다.

Strategy for Computing the Infinite-Width NTK

위에서 MLP에 적용한 NTK Decomposition을 일반적인 방법론으로 설명하고자 한다.

The Canonical Decomposition

NTK Decomposition에 대해서 일반적인 방법론으로 설명하고자 한다.

우선 준비물을 알아보자. 일단 $\xi \in \mathbb{R}^d$를 입력으로 하고 출력은 scalar인 신경망 \(f(\xi)\)가 필요하다. 신경망 \(f(\xi)\)은 weight \(W \in \mathbb{R}^{n\times m}\)과 bias \(b \in \mathbb{R}^{n}\) 으로 이루어져있으며, 어떤 벡터 \(y(\xi) \in \mathbb{R}^n\), \(z(\xi) \in \mathbb{R}^m\)에 대해서 \(y(\xi) = W z(\xi)\) 형식으로 이루어진다. 그동안 다루었던 MLP를 예로 들면 레이어 \(l\)에 대해서 \(y(\xi) = h^l (\xi), z(\xi) = x^{l-1}(\xi)\)라고 할 수 있으며 모든 weight들이 같다면 (\(W^1 = W^2 = \cdots = W^L\)) \((y,z) = \{ (h^2, x^1), \dots, (h^L, x^{L-1})\}\)이라고 할 수 있다.

\(W\)를 바로 사용하기보다 \(\omega \in \mathbb{R}^{n\times m}\)에 대해 \(W = \dfrac{1}{\sqrt{m}} \omega\)라고 factorize한 뒤 \(\omega\)에 포커싱한다. 이런 경우 \(f\)에 대한 NTK \(\Theta\)는 다음과 같이 sum의 형태로 나타나게 된다.

\[\begin{align} \Theta(\xi, \bar{\xi}) = \sum_\omega \langle \nabla_\omega f(\xi), \nabla_\omega f(\bar{\xi}) \rangle + \sum_b \langle \nabla_b f(\xi), \nabla_b f(\bar{\xi}) \rangle \end{align}\]

MLP의 경우, \(W^1 = W^2 = \cdots = W^L \in \mathbb{R}^{n \times n}\)와 \(W=\dfrac{1}{\sqrt{n}} \omega\)에 따라서, \(\nabla_\omega f(\xi) = \dfrac{1}{n} \sum_{l=1}^{L-1} dh^{l+1} x^{l \mathsf{T}}\) 이고 다음과 같이 분해했다.

\[\begin{align*} \langle \nabla_\omega f(\xi), \nabla_\omega f(\bar{\xi}) \rangle &= \dfrac{1}{n^2} \langle \sum_{l=1}^{L-1} dh^{l+1}x^{l \mathsf{T}}, \sum_{\mathscr{l}=1}^{L-1} d\bar{h}^{\mathscr{l}+1}\bar{x}^{\mathscr{l} \mathsf{T}} \rangle\\ &= \dfrac{1}{n^2} \sum_{l,\mathscr{l}=1}^{L-1} \langle dh^{l+1}x^{l \mathsf{T}}, d\bar{h}^{\mathscr{l}+1}\bar{x}^{\mathscr{l} \mathsf{T}} \rangle \\ &= \sum_{l,\mathscr{l}=1}^{L-1} \dfrac{dh^{l+1 \mathsf{T}} d\bar{h}^{\mathscr{l+1}}}{n} \dfrac{x^{l \mathsf{T}} \bar{x}^{\mathscr{l}}}{n} \end{align*}\]

일반적인 케이스로 확장하면, \(f\)의 두 입력 \(\xi, \bar{\xi}\)에 대해서 \(\bar{y} = y(\bar{\xi}), \bar{z} = z(\bar{\xi}), dy=\sqrt{n}\nabla_y f(\xi), d\bar{y} = \sqrt{n} \nabla_\bar{y} f(\xi)\)라고 하면, \(\nabla_\omega f\)는 다음과 같이 표현된다.

\[\begin{align} \langle \nabla_\omega f(\xi), \nabla_\omega f(\bar{\xi}) \rangle &= \dfrac{1}{m} \langle \nabla_W f(\xi), \nabla_W f(\bar{\xi}) \rangle \\ &= \dfrac{1}{mn} \left\langle \sum_{y,z} dy \; z^\mathsf{T}, \sum_{\bar{y},\bar{z}} d\bar{y} \; \bar{z}^\mathsf{T} \right\rangle \\ &= \dfrac{1}{mn} \sum_{y,z,\bar{y}, \bar{z}} \langle dy \; z^\mathsf{T}, d\bar{y} \; \bar{z}^\mathsf{T} \rangle \\ &= \sum_{y,z,\bar{y}, \bar{z}} \dfrac{dy^{\mathsf{T}} d\bar{y}}{n} \dfrac{z^\mathsf{T} \bar{z}}{m} \end{align}\]

이 summation은 \(y=Wz, \bar{y} = W \bar{z}\)를 포함한 모든 행렬 곱셈에 대해서 이루어진다.

\(w\)와 \(b\)가 NTK parameterization에 의해 standard Gaussian 분포에서 추출된다면 \(\dfrac{dy^{\mathsf{T}} d\bar{y}}{n}\)와 \(\dfrac{z^\mathsf{T} \bar{z}}{m}\)가 각각 determinisitc하게 limit \(D^{y,\bar{y}} (\xi, \bar{\xi})\), \(C^{y,\bar{y}} (\xi, \bar{\xi})\)로 수렴할 것이다. (다음 섹션에서 증명할 예정) 마찬가지로 \(\nabla_b f(\xi), \nabla_\bar{b} f(\bar{\xi})\)도 \(D^b (\xi, \bar{\xi})\)로 수렴한다면 Limiting NTK Kernel \(\mathring{\Theta}\)은 다음과 같이 정리된다.

\[\begin{align} \mathring{\Theta} (\xi, \bar{\xi}) = \sum_{\textrm{weight} W} \sum_{\substack{y,z:y=Wz \\ \bar{y},\bar{z}:\bar{y}=W\bar{z}}} D^{y,\bar{y}} (\xi, \bar{\xi}) C^{y,\bar{y}} (\xi, \bar{\xi}) + \sum_{\textrm{bias } b} D^b (\xi, \bar{\xi}) \end{align}\]

\(C\)와 \(D\)를 구하는 직관적인 규칙들

결국 NTK Decomposition은 \(C\)와 \(D\)를 어떻게 구하냐의 문제로 귀결된다. GIA Check Condition을 만족한다면 (output layer가 독립적으로 샘플링 되고 zero mean을 가진다면), 이번 섹션에서 다루는 직관은 \(C\)와 \(D\)를 계산하는데 있어 핵심적인 아이디어이다.

Wide Neural Network를 가정하자. (width \(n >> 1\)) (pre-)activation vector \(x \in \mathbb{R}^n\)는 roughly i.i.d. coordinate을 가지고 있다고 할 수 있으며 이 coordinate들은 랜덤 변수 \(Z^x\)에서 추출되었다고 표현한다. 이는 벡터의 원소의 분포가 roughly i.i.d.라는 말과 다름 없지만 벡터의 성분이 하나의 coordinate처럼 생각할 수 있기에 표현할 수 있는 말이다. 하지만 \(x \in \mathbb{R}^n\)에 대한 랜덤변수 집합 \(\{Z^x \}_x\)은 correlated되었을 가능성이 있다. 그것은 좌표 \(\alpha \in [n]\)에 대해 \(\{ x_\alpha \}_x\)가 이미 correlated되어있을 수 있기 때문이다. 하지만, \(\alpha\)에 대해 roughly i.i.d.를 만족한다.

따라서 \(n \rightarrow \infty\)일 때, 벡터 \(x, y \in \mathbb{R}^n\)은 다음 식을 만족하며 이것은 \(C\)와 \(D\)를 구할 때 필요한 형태이다.

\[\begin{align} x^\mathsf{T} y / n \rightarrow \mathbb{E} Z^x Z^y \end{align}\]

복잡해보인다. 그러나 설명을 좀 더 하자면 결국 우리가 원하는 것은 \(x^\mathsf{T} y / n\)의 형태를 어떻게 구하냐이고, 이는 roughly i.i.d.를 만족하는 랜덤변수 \(Z\)에 의해 기대값으로 표현될 수 있다. \(x\)와 \(y\)를 곱하고 이를 \(n\)으로 나누는 것은 기대값(평균)을 구하는 것과 큰 차이가 없다.

따라서, 다음과 같은 2가지 규칙을 이용하여 activation function에 해당하는 Nonlin규칙과 Weihgt에 해당하는 MatMul규칙을 정의하고 이를 이용하면 재귀적으로 \(Z^x\)를 계산할 수 있어 \(C\)와 \(D\)를 구할 수 있다.

1. Nonlin 어떤 고정된 \(k\) (\(n\rightarrow \infty\)일때의 constant)에 대해서 \(\phi : \mathbb{R}^k \rightarrow \mathbb{R}\) 함수에 대해서 다음과 같이 표현될 수 있다. \(\begin{align} Z^{\phi(x^1, \dots, x^k)} = \phi(Z^{x^1}, \dots, Z^{x^k}) \end{align}\)
2. MatMul \(\mathbb{R}^n\)의 벡터의 집합 \(\mathcal{X}\)와 행렬 \(W \in \mathbb{R}^{n\times n}\)이 있을 때, \(W_{\alpha \beta} \sim \mathcal{N}(0, \sigma_W^2 /n )\)을 만족하면 다음과 같은 랜덤변수 \(\{Z^{Wx} : x\in\mathcal{X}\}\)은 jointly Gaussian이고 zero mean을 만족하며 다음과 같은 covariance를 가진다. \(\begin{align} \mathrm{Cov}(Z^{Wx}, Z^{W\bar{x}}) = \sigma_W^2 \mathbb{E} Z^{x} Z^{\bar{x}}, \textrm{ for any } x, \bar{x} \in \mathcal{X} \end{align}\) 만약, 또 다른 \(\mathbb{R}^n\) 벡터 집합 \(\mathcal{Y}\)가 있고 \(W \neq \bar{W}\)이면, \(\{Z^{Wx} : x\in\mathcal{X}\}\)는 \(\{Z^{\bar{W}y} : y\in\mathcal{Y}\}\)와 독립적이다.

여기에 몇 가지 Remark가 더 붙는다.

• Remark 6.1. 규칙 2번은 \(W\)가 \(\mathcal{X}\)의 벡터와 correlated되더라도 성립한다. 예를 들면, \(x, \bar{x} \in \mathcal{X}\)일 때 \(x=W\bar{x}\) 이거나 \(x=W^\mathsf{T} \bar{x}\)여도 성립한다.
• Remark 6.2. 규칙 2번에서 \(\bar{W} = W^\mathsf{T}\)이면, \(\{Z^{\bar{W}y} : y\in\mathcal{Y}\}\)와 \(\{Z^{Wx} : x\in\mathcal{X}\}\)은 독립적이라는 의미이다. 이는 GIA Simple Check Condition에 따라 GIA가 적용되는 원리와 같다.
• Remark 6.3. 고정된 차원의 입력 \(\xi\)을 Wide neural network 계산하기 위해서, 위의 규칙들을 \(\xi\)에 바로 적용하지 않고 첫번쨰 레이어 임베딩인 \(W \xi \in \mathbb{R}^n\)부터 적용한다.

규칙 1번 Nonlin은 쉽게 이해할 수 있다. nonlinear function을 적용한 벡터 \(x^i\)들의 집합 \(Z\)나 각 집합 \(Z^{x^i}\)에 nonlinear function을 적용한 것들을 비교하나 전체 집합으로 보면 같기 때문이다.

규칙 2번 MatMul 또한 Limit of Foward Quantities \(x^{l \mathsf{T}} \bar{x}^{l} / n^l\) 섹션에서 봤던 직관을 생각하면 이해할 수 있다. Weight \(W \in \mathbb{R}^{n \times n}\)가 \(W_{\alpha \beta} \sim \mathcal{N}(0, \sigma_W^2 /n)\)을 따를 때 zero mean을 유지하는 선형 변환(linear transformation)은 기존 입력값 $x$의 분포를 바꾸지 못한다. 따라서 공분산을 계산할 때 \(Z^{Wx}\)대신에 \(Z^x\)를 써도 무방하고 zero mean이기 때문에 forward quantities 섹션에서 다음 식과 같이 covariance를 구했던것과 같은 직관을 사용할 수 있다.

\[\begin{align} \mathrm{Cov}(x^l_\alpha, \bar{x}^l_\alpha) &= \mathrm{Cov}(\phi(\xi), \phi(\bar{\xi}) \\ &= \mathbb{E}(\phi(\xi), \phi(\bar{\xi}) - \mathbb{E}(\phi(\xi))\mathbb{E}(\phi(\bar{\xi}) \\ &= \mathbb{E}(\phi(\xi), \phi(\bar{\xi}) \end{align}\]

Remark 6.1.의 경우에는 roughly i.i.d.이기 때문에 가능한 것이다. Remark 6.2.의 경우는 \(\bar{W} \equiv W^{\mathsf{T}} \neq W\)이기 때문에 \(\mathcal{Y}\)와 독립이라고 할 수 있다. Remark 6.3.의 경우는 \(\xi\)는 특정 차원에 고정되어있기 때문에 해당 룰을 바로 적용하기 힘들다. 그러나, weight는 Wide network를 가정하고 있기 때문에 첫번쨰 레이어만 한번 변환을 거치고 적용할 수 있다. 그렇게 되면 induction에 의해 나머지 레이어도 같은 룰을 적용할 수 있다.

RNN

위의 룰을 RNN에 적용해보자. RNN은 시간 \(t\)에 대해 현재의 입력 \(\xi^t\)과 이전 상태(state) \(s^{t-1}\)에 기반해서 현재 상태(state) \(s^t\)를 다음과 같이 업데이트 된다.

\[\begin{align} s^t (\xi) = \phi(g^t (\xi) + u^t (\xi) + b), \; g^t(\xi) = W s^{t-1} (\xi), \; u^t(\xi) = U \xi^t \end{align}\]

추가적인 기호를 설명하자면 input sequence는 \(\xi = \{ \xi^1, \dots, \xi^t, \dots, \xi^t \in \mathbb{R}^d \}\), nonlinear activation function을 \(\phi\), weight는 \(W \in \mathbb{R}^{n \times n}, U \in \mathbb{R}^{n \times d}\), 그리고 bias \(b \in \mathbb{R}^n\)이다. 출력을 위한 output weight를 \(v \in \mathbb{R}^n\)이라고 하면 최종 시간 \(T\)에서의 상태 \(s^T (\xi)\)와 결합한 RNN의 output은 \(v^{\mathsf{T}} s^T (\xi) \in \mathbb{R}\)이라고 할 수 있다. 이전과 마찬가지로, 각 weight들이 다음과 같은 분포를 따른다고 하자. \(W_{\alpha \beta} \sim \mathcal{N}(0, 1/n), U_{\alpha \beta} \sim \mathcal{N}(0, 1/d), b_\alpha \sim \mathcal{N} (0, 1), v_\alpha \sim \mathcal{0, 1}\). 그러면 Condition 1은 자동으로 만족하고 위에서 언급한 Nonlin과 MatMul 규칙도 만족한다.

또 다른 input \(\bar{\xi} = \{ \bar{\xi}^1, \dots, \bar{\xi}^t, \dots, \bar{\xi}^t \in \mathbb{R}^d \}\)도 가정해 볼 수 있다. 물론, \(\xi = \bar{\xi}\)도 가능하다. 이제 지금까지의 규칙을 적용해서 NTK Decomposition을 수행하면 된다. RNN에서의 weight matrix는 \(W\)와 \(U\) 두 개가 있다. 각각 기존의 룰을 적용해서 문제를 정의해보면 다음과 같다. 우선 \(W\)은 \(g^t(\xi) = W s^{t-1} (\xi)\)을 만족하므로 이전에 살펴보았던 double sum(\(\sum_{y,z}, \sum_{\bar{y}, \bar{z}}\))처럼 표현해 볼 수 있다.

\[\begin{align*} \langle \nabla_\omega f(\xi), \nabla_\omega f(\bar{\xi}) \rangle = \sum_{y,z,\bar{y}, \bar{z}} \dfrac{dy^{\mathsf{T}} d\bar{y}}{n} \dfrac{z^\mathsf{T} \bar{z}}{m} \end{align*}\]

위 식을 \(\{g^t, s^{t-1}\}, \{\bar{g}^t, \bar{s}^{t-1}\}\)에 대해 적용하면, 우리가 풀어야할 문제는 어떤 sequence \(t\)와 \(r\)에 대해서 \(\dfrac{s^{t \mathsf{T}} \bar{s}^r}{n}, \dfrac{g^{t \mathsf{T}} \bar{g}^r}{n}\)을 푸는 것으로 환원된다. 마찬가지로, weight \(U\)는 \(u^t(\xi) = U \xi^t\)이므로, \(\{u^t, \xi^{t-1}\}, \{\bar{u}^t, \bar{\xi}^{t-1}\}\)에 대해 double sum의 형태로 바꾸면, \(\dfrac{u^{t \mathsf{T}} \bar{u}^r}{n}, \dfrac{\xi^{t \mathsf{T}} \bar{\xi}^r}{d}\)을 구하는 것으로 바뀌지만 \(\dfrac{\xi^{t \mathsf{T}} \bar{\xi}^r}{d}\)은 weight가 아니라서 constant이므로 계산할 필요가 없다.

Forward

섹션 “\(C\)와 \(D\)를 구하는 직관적인 규칙들”에서 나온 프레임워크를 적용하기 위해서는 벡터들과 행렬들을 랜덤변수 \(Z\)로 변환해야 한다. 우선, 고정된 input dimension \(d\)가 있고, vector dimension \(n \rightarrow \infty\)라고 해보자. \(g^t, u^t, s^t, b\)는 \(Z^{g^t}, Z^{u^t}, Z^{s^t}, Z^{b}\)에서 추출한 i.i.d. coordinate를 가지고 있다고 생각한다, 이 말은 앞서 언급했던 것처럼 i.i.d. 변수라는 의미와 같다. 이제 하나씩 살펴보자. 가장 간단한 변수는 \(b\)이다. \(Z^b = \mathcal{N} (0, 1)\)이라고 할 수 있다. 그 다음은 \(u\)이다. \(\{Z^{u^t}, Z^{\bar{u}^t}\}\)는 zero mean을 가지고 covariance \(\mathrm{Cov}(Z^{u^t}, Z^{\bar{u}^t) = \xi^{t \mathsf{T}} \bar{\xi}^r /d\)를 가지는 jointly Gaussian 분포라고 할 수 있다. 지금까지는 Canonical Decomposition에서 MLP example과 같이 비교적 쉽게 이해할 수 있는 방법으로 적용한 것이고, 그 다음은 vector에서 vector로 변환하는 \(g^t(\xi) = W s^{t-1} (\xi)\)과 같은 경우에도 적용해야한다. MatMul 규칙을 적용하면 \(\{Z^{g^t}, Z^{\bar{g}^r}\}\)는 zero mean에 다음과 같은 Covariance를 가지고 있다.

\[\begin{align} \mathrm{Cov}(Z^{g^t}, Z^{\bar{g}^r}) = \mathbb{E} Z^{s^{t-1}}, Z^{\bar{s}^{r-1}} \end{align}\]

이 모든 것을 종합하면 MLP에서 \(C^l (\xi, \bar{xi})\)를 구했던 것과 같은 방식을 통해 다음과 같이 재귀식 형태로 정리할 수 있다.

\[\begin{align} \mathbb{E} Z^{s^{t}}, Z^{\bar{s}^{r}} &= \mathbb{E} \phi(Z^{g^{t}} + Z^{u^{t}} + Z^{b}) \phi(Z^{\bar{g}^{r}} + Z^{\bar{u}^{r}} + Z^{b}) \\ &= \mathbb{E} \phi (\xi_1) \phi (\xi_2) \\ \textrm{where } (\xi_1, \xi_2) &\sim \mathcal{N} \left(0, \mathbb{E} \begin{pmatrix} \left(Z^{s^{t-1}}\right)^2 & Z^{s^{t-1}} Z^{\bar{s}^{r-1}} \\ Z^{\bar{s}^{r-1}} Z^{s^{t-1}} & \left(Z^{\bar{s}^{r-1}}\right)^2 \end{pmatrix} + \dfrac{\xi^{t \mathsf{T}} \xi^r}{d} + 1 \right) \end{align}\]

이를 통해 limit \(C^{s^t, \bar{s}^r} (\xi, \bar{\xi})\)은 다음과 같이 계산된다.

\[\begin{align} C^{s^t, \bar{s}^r} (\xi, \bar{\xi}) = \lim_{n \rightarrow \infty} \dfrac{s^{t \mathsf{T}} \bar{s}^r }{n} = \mathbb{E} (Z^{s^t} Z^{\bar{s}^r}) \end{align}\]

Backward

위에서 Backpropagation을 돌아봤듯이, RNN의 backpropagation은 다음과 같이 정의할 수 있다.

\[\begin{align} d s^{t-1} = W^{\mathsf{T} dg^t, \; dg^{t} = du^t = \phi'(g^t + u^t + b) \odot d s^t \end{align}\]

MLP에서 처럼 \(d s^t\)는 \(W\)때문에 의존성이 걸려서 strict하게 i.i.d.라고 생각할 수 없지만 기존 논문의 가정을 이용하여 i.i.d.라고 가정한다. 따라서, \(d s^t\)를 \(Z^{ds^t}\)에서 추출된 i.i.d. coordinate라고 생각할 수 있고, 다음을 만족한다.

\[\begin{align} \mathbb{E} Z^{ds^t} Z^{d\bar{s}^r} &= \mathbb{E} Z^{du^{t+1}} Z^{d\bar{u}^{r+1}} \\ &= \mathbb{E} \phi'(Z^{g^{t+1}} + Z^{u^{t+1}} + Z^{b}) Z^{ds^{t+1}} \phi'(Z^{\bar{g}^{r+1}} + Z^{u^{r+1}} + Z^{b}) Z^{d \bar{s}^{r+1}} \\ &= \mathbb{E} Z^{ds^{t+1}} Z^{d \bar{s}^{r+1}} \mathbb{E} \phi'(Z^{g^{t+1}} + Z^{u^{t+1}} + Z^{b}) \phi'(Z^{\bar{g}^{r+1}} + Z^{u^{r+1}} + Z^{b}) \\ &= \mathbb{E} Z^{ds^{t+1}} Z^{d \bar{s}^{r+1}} \mathbb{E} \phi'(\xi_1) \phi'(\xi_2) \\ \textrm{where } (\xi_1, \xi_2) &\sim \mathcal{N}\left(0, \mathbb{E} \begin{pmatrix} \left(Z^{s^{t}}\right)^2 & Z^{s^{t}} Z^{\bar{s}^{r}} \\ Z^{\bar{s}^{r}} Z^{s^{t}} & \left(Z^{\bar{s}^{r}}\right)^2 \end{pmatrix} + \dfrac{\xi^{t \mathsf{T}} \xi^r}{d} + 1 \right) \end{align}\]

마찬가지로, 위의 재귀식은 다음과 같은 limit \(D^{s^t, \bar{s}^r} (\xi, \bar{\xi})\)은 다음과 같이 정리된다\dots

\[\begin{align} & D^{s^t, \bar{s}^r} (\xi, \bar{\xi}) = \lim_{n \rightarrow \infty} \dfrac{ds^{t \mathsf{T}} d\bar{s}^r }{n} = \mathbb{E} Z^{ds^t} Z^{\bar{ds}^r}\\ &= D^{u^{t+1}, \bar{u}^{r+1}} (\xi, \bar{\xi}) = \lim_{n \rightarrow \infty} \dfrac{du^{t+1 \mathsf{T}} d\bar{u}^{r+1} }{n} = \mathbb{E} Z^{du^{t+1}} Z^{\bar{du}^{r+1}} \end{align}\]

이렇게 \(C\)와 \(D\)를 알았으니, 다음 식을 이용해서 NTK를 구할 수 있다.

\[\begin{align} \mathring{\Theta} (\xi, \bar{\xi}) = \sum_{\textrm{weight} W} \sum_{\substack{y,z:y=Wz \\ \bar{y},\bar{z}:\bar{y}=W\bar{z}}} D^{y,\bar{y}} (\xi, \bar{\xi}) C^{y,\bar{y}} (\xi, \bar{\xi}) + \sum_{\textrm{bias } b} D^b (\xi, \bar{\xi}) \end{align}\]

Simple GIA Check의 중요성

Simple GIA Check Condition은 output layer가 다른 레이어들의 모든 파라미터와 독립이어야 하고, 내트워크 내부의 다른 파트에서 사용하지 않는다는 조건이다.

Simple GIA Check을 만족하지 않는 경우

예를 들어, 마지막 임베딩 레이어의 평균을 내서 output으로 삼는다면 이 조건이 깨지게 된다. 만약 평균이 내면 어떻게 GIA에 작용되는지 살펴보자.

심플하게 2-hidden-layer network를 가정하자

\[\begin{align} x^1 &= W^1 \xi + 1 \\ h^2 &= W^2 x^1 \\ x^2 &= \phi(h^2) \\ y &= \mathbb{1}^\mathsf{T} x^2 / n \\ \phi(z) &= z^2 \end{align}\]

각 벡터와 행렬의 차원은 다음과 같다. \(\xi = 0 \in \mathbb{R}^d, y\in \mathbb{R}, x^1, h^2, x^2 \in \mathbb{R}^n, W^1 \mathbb{R}^{n\times d}, W^2 \in \mathbb{R}^{n\times n}, W^1_{\alpha \beta} \sim \mathcal{N} (0, 1/d), W^2_{\alpha \beta} \sim \mathcal{N} (0, 1/n)\) 만약에 \(dx^2 = n \dfrac{dy}{dx^2}\)부터 시작하면, backpropgation은 다음과 같이 정리할 수 있다.

\[\begin{align*} dx^2 = 1, dh^2 = 2h^2 \odot 1 = 2h^2, dx^1 = W^{2 \mathsf{T}} dh^2 = 2W^{2 \mathsf{T}} h^2 = 2W^{2 \mathsf{T}} W^{2} x^2 \end{align*}\]

MatMul 에 의해서 \(h^2\)는 \(Z^{h^2} = \mathcal{N} (0, 1)\)에서 추출한 coordinate를 가진다고 할 수 있고, \(dh^2\)또한 \(Z^{dh^2} = 2Z^{h^2} = \mathcal{N}(0, 2)\)에서 추출한 coordinate라고 할 수 있다.

기존 가정을 그대로 사용해서 \(W^{2 \mathsf{T}}\)와 \(W^2\)가 독립이라고 하자. 그러면 \(dx^1\)또한 \(\mathcal{N}(0, 2)\)에서 추출한 coordinate가 되어야 한다. 그러나, 다음과 같은 식을 통해 \(\mathbb{E} dx^1\)는 \(0\)이 되지 않는다.

\[\begin{align*} \mathbb{E} dx^1_\alpha &= 2 \mathbb{E} \sum_{\beta, \gamma} W^2_{\beta \alpha} W^2_{\beta \gamma} x^1_\gamma \\ &= 2 \sum_\beta \mathbb{E} \left((W^2_{\beta \gamma})^2 x^1_\alpha\right) + 2 \sum_\beta \sum_{\gamma \neq \alpha} \mathbb{E} (W^2_{\beta \alpha} W^2_{\beta \gamma} x^1_\gamma ) \\ &= 2\mathbb{E} x^1_\alpha + 0 \\ &= 2\mathbb{E} x^1_\alpha \\ &= 2 \neq 0 \end{align*}\]

\(\mathbb{E} (W^2_{\beta \gamma})^2 = 1\)을 만족하는 반면, \(W^2_{\beta_\alpha}, W^2_{\beta \gamma}, x^1_\gamma\)가 독립이기 때문에 각각의 기대값의 곱으로 바뀔 수 있고 이는 위의 정의에 따라 0이다. \(2 \sum_\beta \sum_{\gamma \neq \alpha} \mathbb{E} (W^2_{\beta \alpha} W^2_{\beta \gamma} x^1_\gamma) = 2 \sum_\beta \sum_{\gamma \neq \alpha} \mathbb{E} W^2_{\beta \alpha} \mathbb{E} W^2_{\beta \gamma} \mathbb{E} x^1_\gamma = 0\)

Simple GIA Check이 GIA를 만족하는 직관

만약 이전처럼 평균을 내는 것이 아니라 마지막 레이어가 전부 독립이라면, \(v_\alpha \sim \mathcal{N}(0,1)\)에서 추출한 \(v\)를 바탕으로 \(y= v^\mathsf{T} x^2 / \sqrt{n}\) 처럼 되고, Simple GIA Check Condition을 만족하게 된다. \(\mathbb{E} v_b (W^2_{\beta \gamma})^2 x^1_\alpha = \mathbb{E} v_b \mathbb{E} (W^2_{\beta \gamma})^2 \mathbb{E} x^1_\alpha = 0\) 그렇게 되면 \(dx^2 = \sqrt{n} \dfrac{dy}{dx^2}\)에서 시작하는 backpropgation을 다시 계산할 수 있게 된다. (\(v\) 추가)

따라서 마찬가지로 \(dx^1\)의 기대값을 구하게되면 독립인 \(v_\beta\)의 영향때문에 모든 항이 0이 된다.

\[\begin{align*} \mathbb{E} dx^1_\alpha &= 2 \sum_\beta \mathbb{E} \left( v_\beta (W^2_{\beta \gamma})^2 x^1_\alpha\right) + 2 \sum_\beta \sum_{\gamma \neq \alpha} \mathbb{E} (v_\beta W^2_{\beta \alpha} W^2_{\beta \gamma} x^1_\gamma ) \\ &= 0 \end{align*}\]

즉, 마지막 layer가 \(W\)와 \(W^{\mathsf{T}}\)가 서로 연결(correlated)될 가능성을 차단하는 것이다. 이것이 Simple GIA Check Condition이 GIA를 만드는 직관이다.

Conclusion

지금까지, 일반적인 뉴럴 네트워크를 NTK를 확장하는 방법을 알아보았다. 다른 아키텍처를 지니더라도 NTK의 특성을 적용할 수 있는 근거를 마련할 수 있었다.

결국 이 논문을 3줄 요약하면 다음과 같다.

1. NTK는 inner product 2개(forward & backward)의 곱(product)로 표현할 수 있고, 각각을 \(C\)와 \(D\)로 표현하며, 이 둘은 covariance의 limit을 통해 표현 가능하다.
2. GIA를 만족하는 뉴럴 네트워크는 1.처럼 변환할 수 있다. (NTK화) 이걸 쉽게 확인하는 건 NETSOR\(\mathsf{T}\)를 만족하는지만 확인하면 되는데 이는 이 포스트의 한계를 넘어섰기에 생략한다.
3. GIA는 forward와 backward pass에서의 weight들이 서로 관련이 없다는 가정인데, 이는 output layer가 zero mean을 가지고 다른 파라미터(weight)들과 서로 독립적이며, 뉴럴 네트워크 다른 곳에서 사용하지 않는다는 조건만 만족하면 성립한다. 간단하게 말해서 output layer를 평균낸다는가 하는 일을 저지르지 않으면 된다.

근데, Greg Yang은 천재인가? 이걸 혼자 썼다고? 아니다. 그는 천재다.

References

1. Yang, Greg, Edward J Hu, Igor Babuschkin, Szymon Sidor, Xiaodong Liu, David Farhi, Nick Ryder, Jakub Pachocki, Weizhu Chen, and Jianfeng Gao. 2022. “Tensor Programs v: Tuning Large Neural Networks via Zero-Shot Hyperparameter Transfer.” ArXiv Preprint ArXiv:2203.03466.
2. Yang, Greg, James B Simon, and Jeremy Bernstein. 2023. “A Spectral Condition for Feature Learning.” ArXiv Preprint ArXiv:2310.17813.
3. Yang, Greg. 2020. “Tensor Programs Ii: Neural Tangent Kernel for Any Architecture.” ArXiv Preprint ArXiv:2006.14548.
4. ———. 2019. “Wide Feedforward or Recurrent Neural Networks of Any Architecture Are Gaussian Processes.” Advances in Neural Information Processing Systems 32.
5. Jacot, Arthur, Franck Gabriel, and Clément Hongler. 2018. “Neural Tangent Kernel: Convergence and Generalization in Neural Networks.” Advances in Neural Information Processing Systems 31.
6. Poole, Ben, Subhaneil Lahiri, Maithra Raghu, Jascha Sohl-Dickstein, and Surya Ganguli. 2016. “Exponential Expressivity in Deep Neural Networks through Transient Chaos.” Advances in Neural Information Processing Systems 29.
7. Schoenholz, Samuel S, Justin Gilmer, Surya Ganguli, and Jascha Sohl-Dickstein. 2016. “Deep Information Propagation.” ArXiv Preprint ArXiv:1611.01232.
8. Yang, Ge, and Samuel Schoenholz. 2017. “Mean Field Residual Networks: On the Edge of Chaos.” Advances in Neural Information Processing Systems 30.