What is Attention Mechanism? (The Meaning of K, Q, V)
Why K, Q, V?
예전에 Transformer에서 K, Q, V의 의미가 무엇이냐는 질문을 받았을 때 갑자기 머리가 멍해지면서 제대로 답변을 못한 적이 있었다. 그런데 막상 찾아보면, 그 의미를 명확히 전달해주는 글은 잘 없었다. 원래 논문(Vaswani et al. 2017)을 찾아보라고 보통 애기하지만, 이걸 제대로 보려면 (Bengio, Ducharme, and Vincent 2000), (Bahdanau, Cho, and Bengio 2014), (Sutskever, Vinyals, and Le 2014), (Vaswani et al. 2017)로 이어지는 흐름을 전부 이해해야 한다고 생각한다.
과거에 내가 Transformer를 배운건 The Illustrated Transformer를 통해서였지만, 이걸 봐도 그래서 K, Q, V가 뭔데?라는 의문은 여전히 해소하지 못한대로 라이브러리에 구현한걸 그대로 가져다 썼다. 하지만 이제는 그때와 같은 이해도는 아닐뿐더러 리서처 입장에서는 최근 흐름상 점점 더 Transformer의 K, Q, V를 근본적으로 건드리는 논문들도 많아지기 때문에, 엔지니어 입장에서는 KV Cache 같은 걸 적용해야하는 상황이 생기기 때문에 이 문제를 단순 라이브러리 적용으로 해결할 수는 없을 것이다.
그러나 이 질문을 쉽게 설명하기는 힘들다. 굉장한 논문들이지만, 이 많은 논문들을 다 읽고 이해하는건 쉬운 일이 아니기 때문이다.
이에 대해 고민을 하다가 정말 좋은 설명을 찾았다. 최근에 Andrej Karpathy의 NN: Zero to Hero가 그것이다. 이 플레이리스트를 보고 따라하면서, 머리에 해머를 맞은듯한 충격을 받았다. (참고로 딥러닝을 처음 접하는 분들에게 딥러닝을 어떻게 배우냐고 질문이 들어오면 이 플레이리스트를 먼저 추천해주고 싶다.) 내가 그동안 너무 어렵게 생각했던 부분도 있었고, 잘못 생각하고 있던 부분이 있다는걸 깨달았다. 여기에 위 질문에 대한 답이 있었다.
정확히는 Let’s build GPT: from scratch, in code, spelled out.와 Stanford CS25: V2 I Introduction to Transformers w/ Andrej Karpathy가 그 답이었다. 이 두 비디오는 Transformer를 설명하는 최고의 강의라고 생각한다. 그래서 Attention에서 K,Q,V가 어떻게 나오게 되었는지 정리를 해보았다.
Language Model and Text Generation
일단 우리가 생각하는 언어 모델(Language Model)에 대해서 생각해볼 필요가 있다.
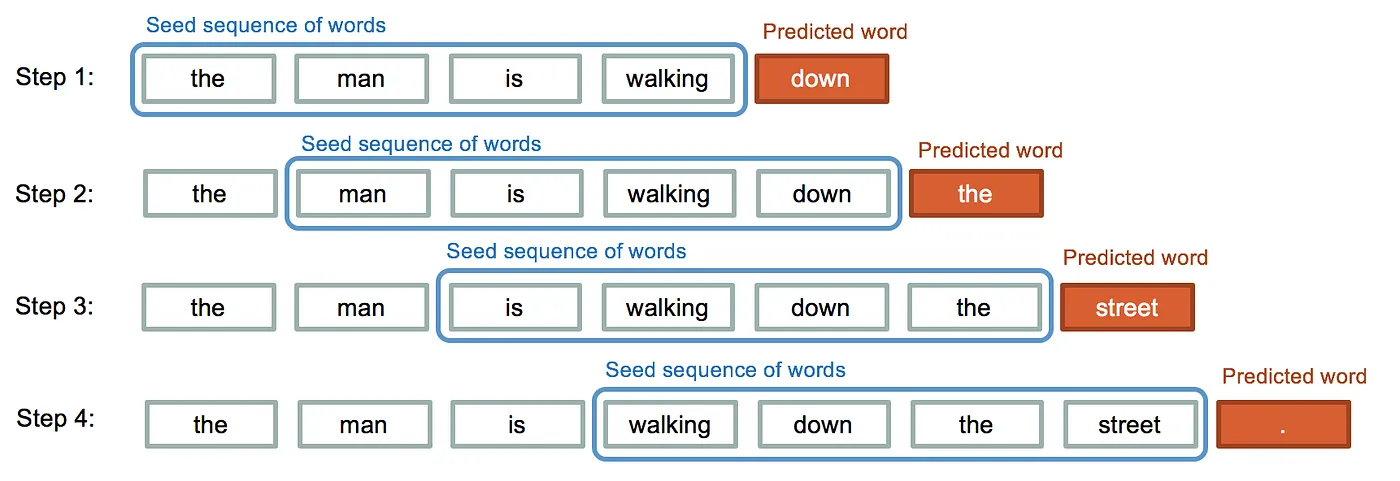
텍스트 생성(Text generation) 관점에서의 언어모델이란, 이전의 문맥(Context)를 통해 다음 단어(실제로 토큰)의 확률 분포를 예측하고, 가장 높은 확률의 단어를 샘플링한 뒤, 가장 높은 확률의 단어를 생성한다고 볼 수 있다.
이 때 할 수 있는 질문은 다음과 같다.
- 단어만으로 충분한가?
- 단어의 확률은 어떻게 계산할 수 있는가?
Text to Numbers
단어만으로 충분한가?
그럴수도 있고, 아닐 수도 있다.
Hello, World! My name is blah blah. Let’s delve deep into the meaning of transformer. Language Model is so capricious!
같은 문장이 있을때, My나 name같은 단어는 쉬우니까 하나로 생각할 수 있지만, capricious같은 단어는 하나의 단어로 생각할수도 있고 뒷부분의 ous같은 부분은 다른데서도 재사용가능하니까 쪼갤 수 있어보인다. 이렇게 단어보다 조금 더 잘게 쪼갠 파트를 모델에서 숫자로 변환하서 학습하게 된다.
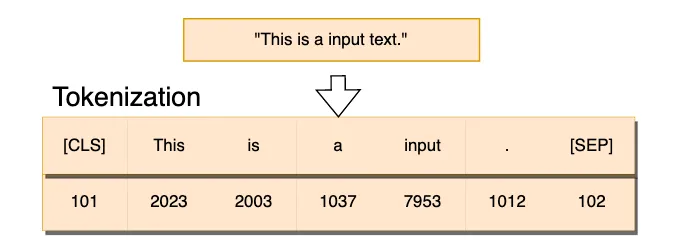
이렇게 문장을 모델에서 사용할 수 있는 단위(토큰, Token)로 만드는것을 토큰화(Tokenize)라고 하고, 그 작업을 해주는 프로그램을 토크나이저(Tokenizer)라고 한다. 단어를 토큰으로 사용할 수도 있지만 이러면 토큰의 수가 너무 많아지기 때문에, 요즘에는 단어보다는 조금 더 작은 단위(subword) 토크나이저를 많이 쓴다.
그래서 실제로 어떻게 나누는 것일까? GPT4는 위 문장을 다음과 같이 분리한다.
한글은 어떨까? 아래를 보면 훨씬 복잡해보인다.
안녕, 세상아! 내 이름은 아무거나야. 트랜스포머에 대해 깊이 파헤쳐 보자! 언어 모델은 너무 변덕스러워
단어의 확률은 어떻게 계산될 수 있는가?
딥러닝을 사용하든, 데이터로부터 단어의 단순 빈도수를 측정하여 확률을 측정하든 단순히 확률을 계산할 할 수 있는 방법은 많다.
언어 모델링은 어떻게 보면 다중 클래스 분류 문제(Multiclass Classification Problem)라고 할 수 있다. 사람도 그렇다. 말을 하다보면 문장의 순서라는게 있고, 갑자기 뜬금없는 단어가 튀어나오는 경우는 잘 없다. 어떤 특정한 단어가 선택지에 있는 것이고, 그 중에서 가장 적절한 단어를 사람이 선택하는 것이다. 모델도 특정 단어셋이 있고, 그 중에서 가장 확률이 높은 단어를 선택한다. 이 때, Cross Entropy를 많이 사용한다.
토크나이저 그리고 임베딩
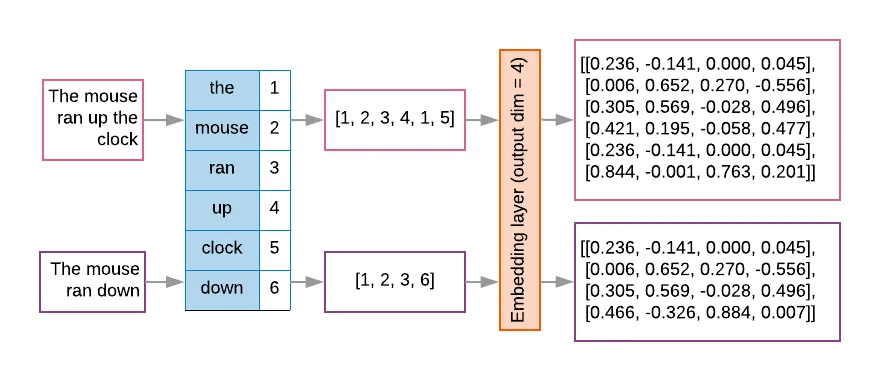
토크나이저는 단어를 더 작은 단위(subword, character chunk)로 쪼개고, 이를 정수(token id)에 매핑한다. 컴퓨터는 문자를 이해하지 못하기 때문에 이렇게 숫자 형태로 변형되어야 계산이 가능하다.
하지만, 이렇게 단순히 하나의 숫자로 표현된 토큰은 정보량이 적다. 토큰의 위치라던가 의미는 다양할 수 있기 때문이다. 따라서 이를 각 토큰을 벡터로 변환하여 임베딩을 생성하게 된다.
Numbers to Generation: Single-head Attention
토크나이저와 임베딩을 활용해서 어떻게든 텍스트를 컴퓨터가 해석할 수 있는 숫자로 바꾸었다. 그럼 다음 토큰은 어떻게 예측되는 것일까? 가장 단순하게 예측하는 방법은 평균을 내는 것이다.
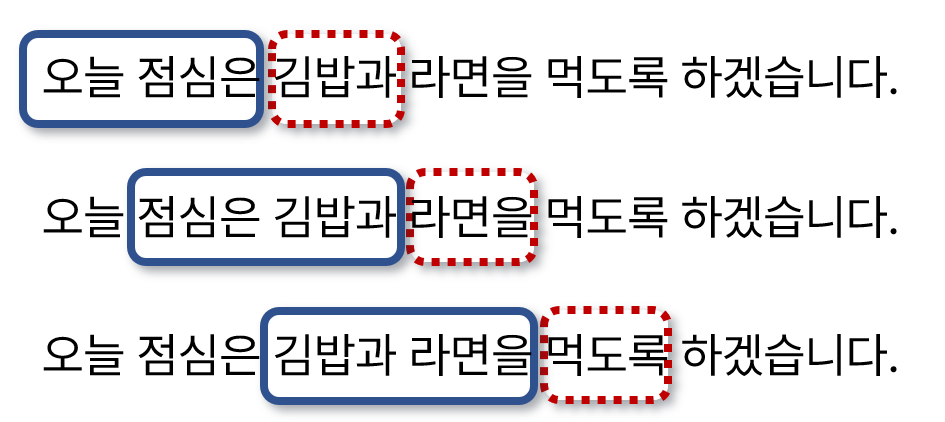
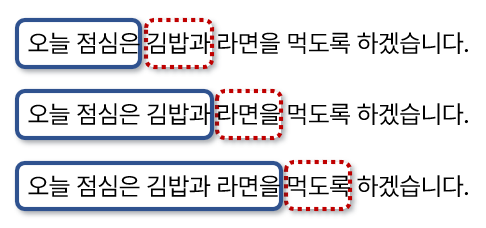
Bigram(이전 2개의 단어를 고려해서 다음 단어를 예측) 모델이 있다고 가정하자. 다음과 같이 이전 단어 (파란색) 2개를 참조해서 다음 단어 (빨간색) 단어를 예측하는 형태라고 보면 된다.
일반적으로 김밥과 라면을 “걷는다” 라고는 하지는 않는다. “걷는다”라는건 김밥과 라면이라는 단어에 비해 확률이 낮은 단어이기 때문이다. 그림처럼 “먹도록”이라는 단어가 더 자연스럽다.
하지만 이럴 경우, 두 단어 이전에 나온 문맥(Context)을 반영하기는 쉽지 않다. 그러기에 다음과 같이 그 이전 단어까지 포함한 문맥을 파악해서 생성할 필요가 있다.
Version 1: Average
가장 간단하게 문맥을 생성하는 방법은 이전 단어들의 평균을 내는 것이다
위 그림을 봐도 이전 단어들에 동등한 가중지(weight)를 줄 뿐이다. 수학적으로 각 단어의 임베딩을 $[\mathbf{x}_0, \mathbf{x}_1, \cdots, \mathbf{x}_n]$라고 표현할 수 있는데, 가중치(weight)와 결합하면 다음과 같이 표현할 수 있다. (elementwise sum)
\[\begin{equation} \mathbf{x_n} = \sum_{i=1}^{n-1} \dfrac{1}{n-1} \mathbf{x_i} \end{equation}\]이 때 가중치(weight) $\textrm{wei}$는 $\dfrac{1}{n-1}$가 된다. 예를 들어 “오늘”이라는 단어의 임베딩이 $[0.1, 0.5]$ 이고, “점심은”이라는 단어의 임베딩은 $[0.6, 0.7]$이라고 하면, “김밥과”라는 단어는 $[0.35, 0.6]$이 되는 것이다.
이를 행렬(matrix) 연산으로 어떻게 표현할까? $\mathbf{x}$가 각 단어를 뜻한다고 가정하고 임베딩 크기(embedding size)를 2라고 가정하자. 그러면 각 행은 $\mathbf{x}{1}$은 *오늘*, $\mathbf{x}{2}$는 점심은 등으로 매핑된다. 한번에 4개의 단어까지 본다고 가정하고(context_size=4 or time_length=4) 임베딩 크기는 2(embed_size=2 or channel_size=2)라고 가정했을 때, $\mathbf{x}$는 $4 \times 2$ 행렬이다.
이 때 다음 단어의 임베딩 예측값은 평균을 나타내는 가중치 행렬 $\textrm{wei}$과의 현재 단어의 임베딩 $x$ 행렬의 곱셈으로 표현이 가능하다.
\[\begin{bmatrix} \mathbf{x}^{'}_2 \\ \mathbf{x}^{'}_3 \\ \mathbf{x}^{'}_4 \\ \mathbf{x}^{'}_5 \\ \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0.5 & 0.5 & 0 & 0 \\ 0.33 & 0.33 & 0.33 & 0 \\ 0.25 & 0.25 & 0.25 & 0.25 \end{bmatrix} \begin{bmatrix} \mathbf{x}_1 \\ \mathbf{x}_2 \\ \mathbf{x}_3 \\ \mathbf{x}_4 \\ \end{bmatrix}\]기호 대신 임베딩 벡터 자체를 넣어서 표현하면 (임베딩 벡터 자체는 랜덤하다)
\[\begin{bmatrix} 0.1 & 0.5 \\ 0.35 & 0.6 \\ 0.33 & 0.693 \\ 0.35 & 0.725 \\ \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0.5 & 0.5 & 0 & 0 \\ 0.33 & 0.33 & 0.33 & 0 \\ 0.25 & 0.25 & 0.25 & 0.25 \end{bmatrix} \begin{bmatrix} 0.1 & 0.5 \\ 0.6 & 0.7 \\ 0.3 & 0.9 \\ 0.4 & 0.8 \\ \end{bmatrix}\]그러면 가중치 행렬 $\textrm{wei}$는 어떻게 만들어야 할까?
\[\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0.5 & 0.5 & 0 & 0 \\ 0.33 & 0.33 & 0.33 & 0 \\ 0.25 & 0.25 & 0.25 & 0.25 \end{bmatrix}\]그것은 1로 채워진 lower triangular matrix에 행별로 더한값을 나눠주면 된다. 코드로는 PyTorch의 tril과 sum을 이용한다.
wei = torch.tril(torch.ones(4, 4))
# [1 0 0 0]
# [1 1 0 0]
# [1 1 1 0]
# [1 1 1 1]
wei = wei / torch.sum(w, 1, keepdims=True)
# [1 0 0 0] / 1.0
# [1 1 0 0] / 2.0
# [1 1 1 0] / 3.0
# [1 1 1 1] / 4.0
Version 2: Matrix Multiplication
여기에 Batch까지 고려하면 batch multiplication까지 갈 수 있다. 현재까지는 $x$를 ($T \times C$) 즉, (time_length $\times$ channel_size) 행렬만 생각했지만, ($B \times T \times C$) 즉, (batch_size $\times$ time_length $\times$ channel_size) 행렬까지 있다고 가정하자.
우리의 $\textrm{wei}$ 행렬은 $T \times T$이므로, $(T \times T) \cdot (B \times T \times C)$ 형태의 곱셈이 된다. PyTorch는 똑똑하기 때문에 $(T \times T)$에 batch dimension를 자동을 추가하여 $(B \times T \times T) \cdot (B \times T \times C) = (B \times T \times C)$ 행렬 곱셈을 수행한다. (Batch Matrix Multiply)
Version 3: Adding Softmax
지금까지는 직접 평균을 냈으나, 이제는 지금까지의 평균과정을 softmax형태로 변환해보고자 한다. 지금은 모든 토큰의 확률이 같고 정해져 있기에 상관없지만, 나중에는 모델을 통해 logit형태로 가중치가 나올것이고 이를 softmax를 이용하여 확률로 변환시키기에 필요하다. 우선 코드를 보자.
PyTorch의 masked_fill과 softmax를 사용하였다.
T = 4
tril = torch.tril(torch.ones(T, T))
wei = torch.zeros(T, T)
# [0 0 0 0]
# [0 0 0 0]
# [0 0 0 0]
# [0 0 0 0]
wei = wei.masked_fill(tril == 0, float('-inf'))
# [0 -inf -inf -inf]
# [0 0 -inf -inf]
# [0 0 0 -inf]
# [0 0 0 0]
wei = F.softmax(wei, dim=-1)
# [1.00 0.00 0.00 0.00]
# [0.50 0.50 0.00 0.00]
# [0.33 0.33 0.33 0.00]
# [0.25 0.25 0.25 0.25]
우선 masekd_fill을 통해 tril의 0인 부분을 -inf로 대체한다. 그리고 softmax를 취하면, -inf는 지수 함수 exp에 의해 0이 되고, 나머지 0값들은 지수함수를 적용하면 1이 되지만 행 별로(dim=-1) 더해진 값에 대해 나눠지므로 위에서 그동안 봤던 $\textrm{w}$랑 동일한 행렬이 된다.
이는 두 가지 의미가 있는데, 우선 현재 단어(or 토큰)는 미래의 단어(or 토큰)을 알지 못한다. 이는 당연하다. 미래의 일을 어찌 알겠는가? 또 다른 의미는 softmax를 이용하면 과거 토큰들이 서로 얼마나 관계를 지니고 있는지 알려준다는 점이다. 예를 들어 어떤 단어는 바로 이전 단어에 강한 영향을 받을 수 있고, 아니면 좀 더 이전의 단어에 영향을 크게 받을 수도 있다. 후자의 대표적인 예시는 대명사의 활용일 때이다. 예를 들면, “홍길동은 조선시대에 태어났다. 그는 의적이었다.”라는 문장에서 그는이라는 단어는 태어났다가 아닌 홍길동은과 더 가까운 단어이다. 수치적인 다른 예시로는 전자는 [0.001, 0.0001, ..., 0.9] 이런식으로 표현할 수 있을 것이고, 후자는 [0.001, 0.7, ..., 0.01] 이런식으로 표현될 수도 있다.
지금까지는 단순 평균을 냈지만, 단순 평균보다는 특정 부분의 단어에 집중하는게 상식적으로 더 맞는말이다. 이를 수학적으로 softmax가 이전 단어들간의 친화도(affinity)를 종합(aggregation)하는 역할을 수행하도록 하는 것이다. 또한 미래 단어의 영향을 배제하게 하기 위해서 -inf를 채워 단절시킨다. 그래서 “어텐션”(Attention) 매커니즘인 것이다. (정확히는 Self-Attention)
Version 4: Self Attention
해당 영상에는 positional encoding얘기도 했지만, 너무 길어지기에 일단 스킵한다. 지금까지는 모든 위치에 대해서 단순 평균을 냈기 때문에 위치를 고려할 필요가 없었다. 그러나 어텐션 메커니즘은 해당 단어 근처가 아닌 먼 위치의 정보가 중요할 수 있기에 위치의 정보도 모델에 포함시킬 필요가 있고, 이를 위해 postional encoding을 사용한다. 하지만 이 이야기를 더 하면 너무 길어지므로 다른 포스트로 따로 작성할 예정이다.
다시 본론으로 돌아오자.
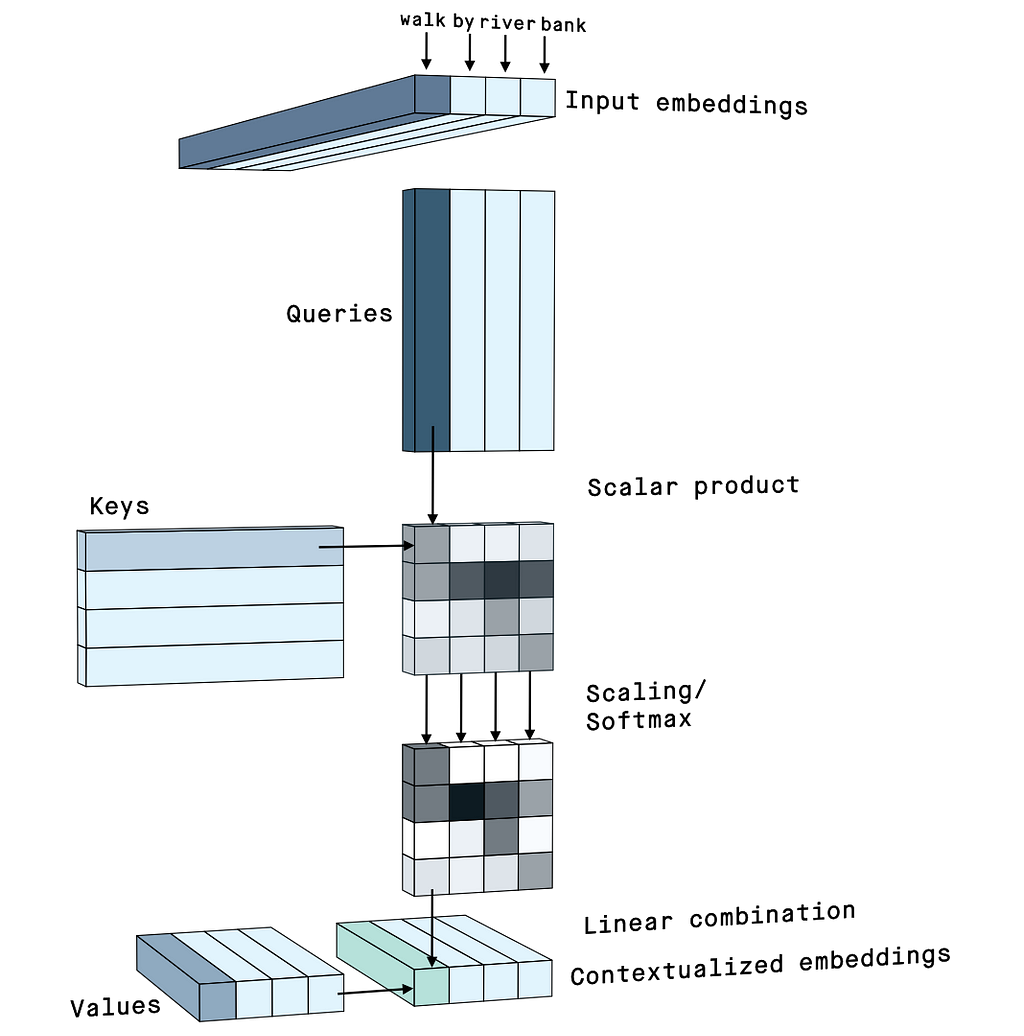
이전까지는 각 토큰(or 단어, 이제는 토큰으로 명칭을 통일한다)의 관계(affinity)는 이전 토큰들의 평균으로 구했다. 그러나 단순 평균만으로는 복잡한 토큰들의 관계를 표현하기에는 부족하다. 그러기에 과거의 토큰의 정보를 가져 오되, 데이터에 기반해서 토큰의 관계를 계산할 필요가 있다.
이를 위해 모든 토큰은 두 벡터, query와 key를 생성한다. Karpathy의 표현을 빌리자면 query vector는 what am I looking for, key vector는 what do I contain이라고 표현하는데 이 표현이 가장 직관적인 설명이라고 생각한다. 한국어로 표현하면 query 벡터는 현재 바라보고 있는 토큰 그 자체(관심 대상)이며, key 벡터는 다른 토큰이 가지고 있는 정보(비교 대상)이다. 토큰간의 친화도(affinity) 혹은 관계란 현재 바라보는 토큰이 다른 토큰들의 정보와 얼만큼 관련있는지에 따라 달라지며, 이는 query가 key와 얼마나 잘 맞는지에 대한 것이라고 할 수 있다. 이를 정량적으로 계산하는 방법은 query과 key간의 내적(dot product)를 통해 가중치를 계산하는 방법이다. 이 가중치, 즉 dot product값이 클 수록 query와 key가 잘 매칭된다는 의미이다.
B, T, C = 4, 8, 32
x = torch.randn(B, T, C) # B=batch_size, T=time_size(token_length), C=channel_size
# single head attention
head_size = 16
key = nn.Linear(C, head_size, bias=False)
query = nn.Linear(C, head_size, bias=False)
k = key(x) # (B, T, head_size)
q = query(x) # (B, T, head_size)
# batch multiplication
wei = q @ k.transpose(-2, -1) # (B, T, head_size) @ (B, head_size, T) = (B, T, T)
# [[[-1.75 2.15 -1.21 0.23],
# [ 0.35 -0.21 -0.56 0.25],
# [ 1.21 -0.91 0.19 2.10],
# [ 0.52 0.21 -0.12 -0.35]],...]
여기서 나오는 wei는 raw affinity 그 자체라고 할 수 있다. 여기에 이전 Version에서 한 것처럼 masking을 통해 미래의 토큰간의 관계를 차단하고, softmax를 취하면 확률을 구할 수 있다.
tril = torch.tril(torch.ones(T, T))
wei = wei.masked_fill(tril == 0, float('-inf'))
wei = F.softmax(wei, dim=-1)
# [[[1.00 0.00 0.00 0.00],
# [0.21 0.79 0.00 0.00],
# [0.14 0.67 0.19 0.00],
# [0.33 0.11 0.21 0.35]],...]
out = wei @ x
하지만 실제로는 query와 key로부터 나온 wei는 token(x)과 다이렉트로 소통하지는 않는다. x대신 value vector 라고 불리우는 v를 사용한다. value vector는 x대신 사용하는, 실제로 친화도(affinity)를 적용할 대상이라고 할 수 있다. 영상에서도 value는 what I communicate to라고 표현하고 있다. 다른 표현으로는 what I will provide라고도 생각할 수 있다. 출처
v = nn.Linear(C, head_size, bias=False)
out = wei @ v
Summary (Single-head Attention)
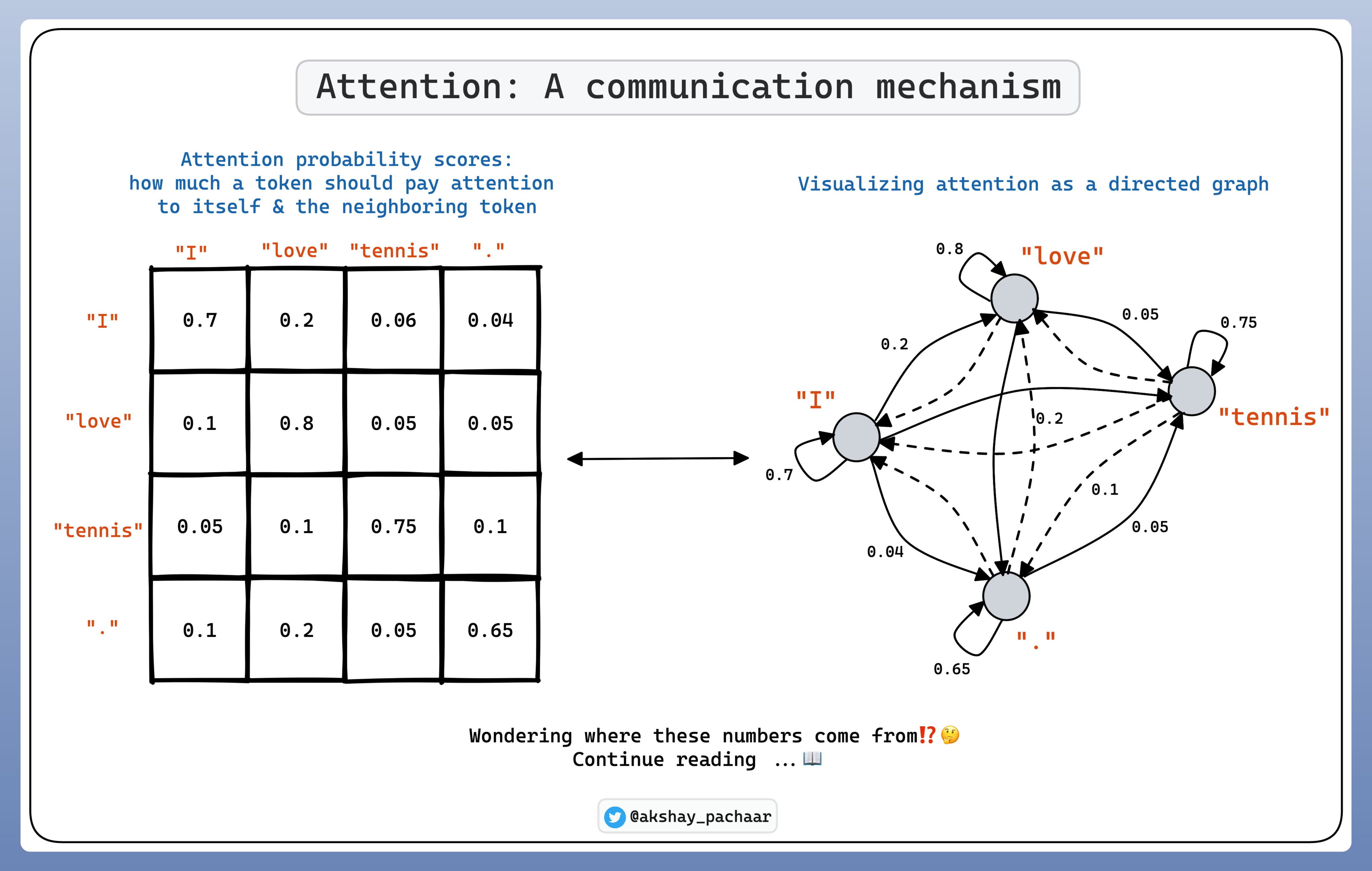
Attention(여기서는 Self-attention) 메커니즘은 데이터 의존적인(data dependent) 커뮤니케이션 메커니즘이다.
일반적인 weight을 사용하게 되면 훈련중에 고정된 weight로 특정 위치의 토큰만 커뮤니케이션하게 된다. 그러나 Attention 메커니즘을 사용하면, 데이터에 따라서 다른 위치의 다른 토큰과 커뮤니케이션을 할 수 있다.
커뮤니케이션은 위의 그림처럼 표현할 수 있다. 각 토큰간의 확률은 위 그림과 같이 그래프로 표현이 되고, 여기서 가장 중요한 것은 왼쪽의 행렬 즉 토큰들간의 attention weights를 구하는 것이다. 이는 다음과 같이 구할 수 있다.
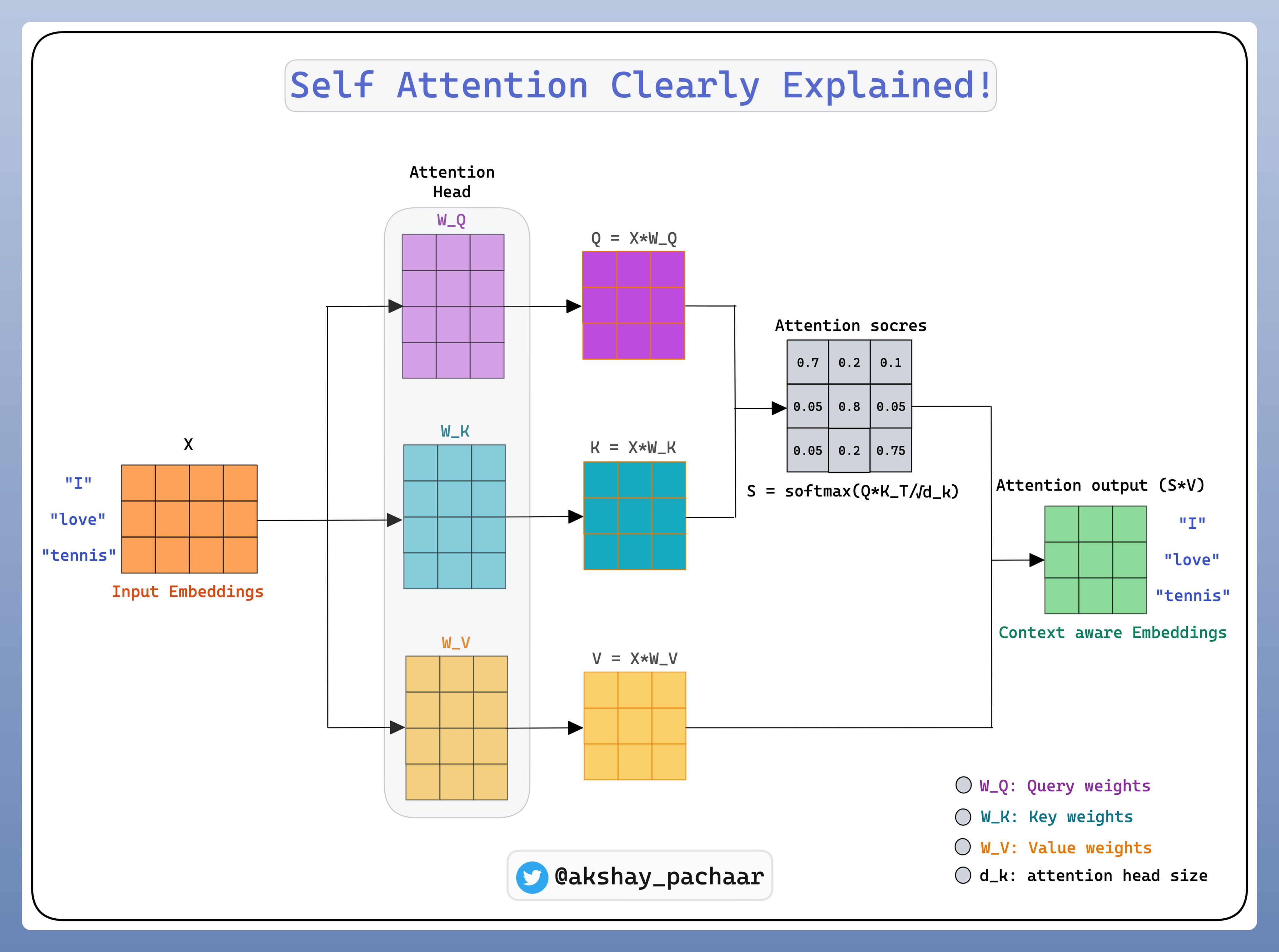
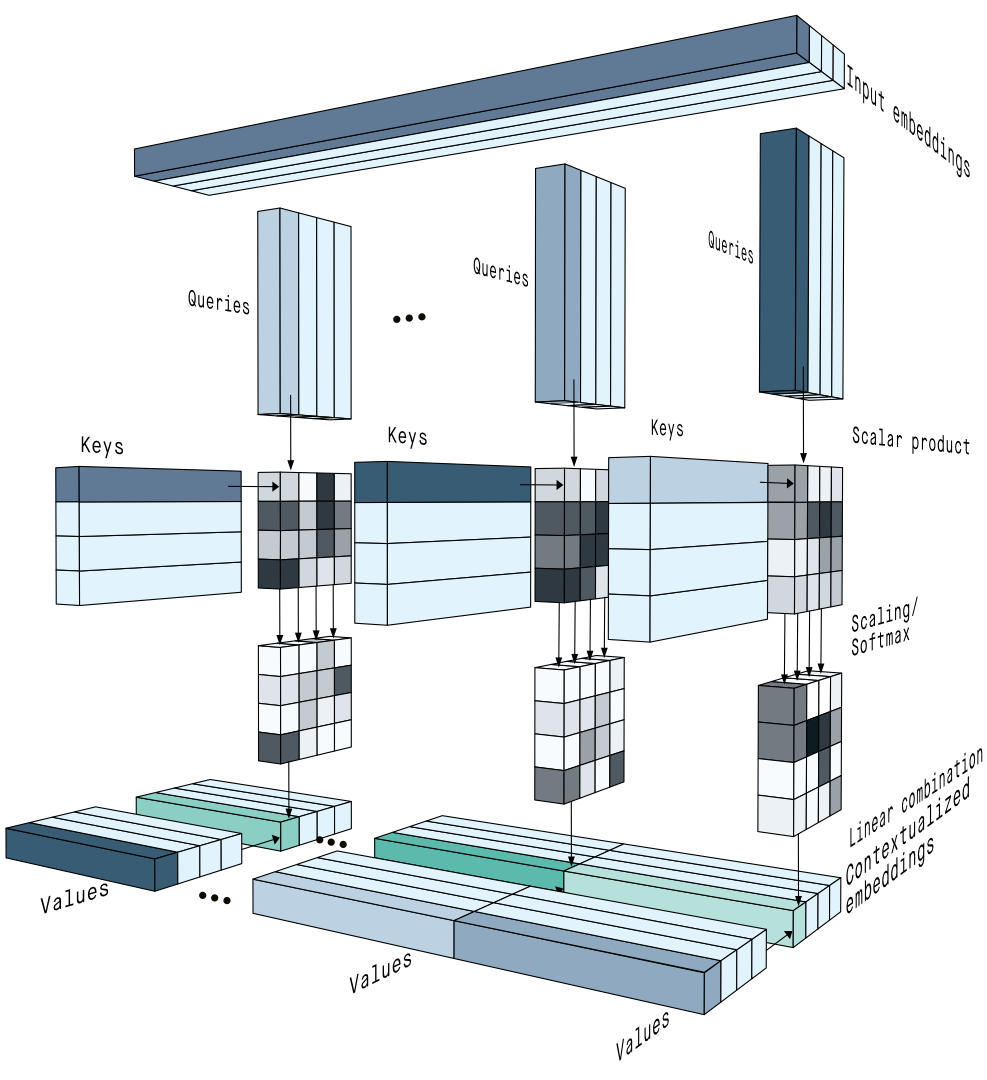
Input Embedding을 $X$라고 할 때, $X$에 weight $W^Q$, $W^K$, $W^V$를 곱해서 $Q, K, V$를 만든다. 이는 어떻게 보면 새로운 임베딩이라고 해석할 수 있다.
배치 사이즈를 $B$, 총 토큰의 사이즈를 $T$, 원래 임베딩 길이를 $d_{model}$(Version 4에서의 $C$)라고 했을 때, $X$의 shape는 $(B, T, d_{model})$ 이라 표현이 가능하다. head size를 $d_k$라고 하면, weight $W^Q$의 shape는 $(d_{model} \times d_k)$, $W^K$는 $(d_{model} \times d_k)$, 그리고 $W^V$는 $(d_{model} \times d_v)$ 라고 할 수 있다. 수학적으로는 (Vaswani et al. 2017) 논문처럼 $W^Q_i \in \mathbb{R}^{d_{model} \times d_k}$, $W^K_i \in \mathbb{R}^{d_{model} \times d_k}$, $W^V_i \in \mathbb{R}^{d_{model} \times d_v}$ 라고 표현한다.
Attention weights를 구하기 위해 먼저 attention scores를 구한다. Attention scores는 i번쨰 토큰이라고 생각할 수 있는 Query $Q_i$를 j번째 토큰이라고 생각할 수 있는 Key $K_j$와 내적(dot product)를 통해 구할 수 있다. attention score는 $(B, T, T)$의 형태로 나타내어지며, 배치 하나의 경우 위 그림의 왼쪽 행렬와 같은 꼴이 된다. 이를 Gradient의 안정성을 위해 attention head size $d_k$를 이용하여 $\sqrt{d_k}$로 scaling한다.
이렇게 만든 attention score를 softmax를 취해서 확률의 형태로 만든다. 이게 attention weights이다. Attention weights는 각 토큰간의 관계를 확률적 가중치로 표현한 것이라고 해석할 수 있다.
마지막으로 이렇게 만든 attention weight와 실제 우리가 적용해야할 $V$와 곱해서 attention output, 즉 데이터 의존적인 (data dependent) context vector를 생성한다. $W^Q, W^K, W^V$는 모델 훈련을 하고 나면 고정된 값이 되지만, attention output은 data에 따라 매번 변한다. 이를 수식과 그림으로 표현하면 다음과 같다.
\[\begin{align} \textrm{Attention}(Q, K, V) = \textrm{softmax}\left( \dfrac{QK^T}{\sqrt{d_k}} \right) V \end{align}\]
Numbers to Generation: More topics
Multi-head Attention
하지만, 하나의 attention score만 의존하는 것보다 다양한 관점에서 attention score를 얻는게 더 우수하다고 생각할 수 있다. 단어 하나가 여러 의미를 가질 수 있는 것은 일반적으로 생각해봤을 때 매우 당연한 이야기이다. 이렇게 여러 개의 key, query, value weights를 통해서 다양한 context를 파악하고자 하는 것이 multi-head attention이다.
이렇게 나눈 key, query, value matrix를 종합적으로 판단하기 위해 병합작업이 필요한데, 원 논문 (Vaswani et al. 2017)에서는 단순히 연결(concatenation)연산을 통해서 수행하였다. 이렇게 해서 얻는 Multi-head attention의 가장 큰 장점은 각 head의 계산은 독립적으로 수행될 수 있다는 점이고, 이는 곧 병렬적으로 수행할 수 있음을 뜻한다.
복잡하게 느껴질 수 잇겠지만, 단순하게 생각하면 기존의 Single-head attention을 하나의 “head”라고 간주하고 여러 번 수행하는 것 뿐이다.
문제는, 여러 개의 key, query, value를 쓰면 당연히 계산 비용(computation cost)가 올라간다. 따라서 새로운 head size를 기존 head size를 head수만큼 나눠서 정한다. 이러면, head를 쪼개서 multi-head attention을 수행하는 것과 동일하므로 계산 비용면에서는 기존과 동일하다.
이를 수식으로 표현하면 다음과 같다.
\[\begin{align} \textrm{MultiHead}(Q, K, V) &= \textrm{Concat}(\textrm{head}_1, \dots, \textrm{head}_n)W^O \\ \textrm{where }\textrm{head}_i &= \textrm{Attention}(Q W^Q_i, K W^K_i, V W^V_i) \end{align}\]그러면 기존의 다음과 같던 Single-head Self Attention Mechanism이
다음과 같이 Multi-head attention 확장된다.
Feed-Forward Network
각 Self Attention head에서 logit을 계산하기 직전에 Feed-Forward Network (MLP + activation function)를 추가한다. 느낌상 하나쯤 넣어주는게 더 안정적이지 않을까 생각했는데, Karpathy의 설명이 너무 좋았다.
위에서 Attention은 커뮤니케이션 메커니즘이라고 설명했다. 각 토큰마다 Self Attention을 적용해서 데이터에 대한 수집은 끝났고, 모델 입장에서는 각 토큰에 대해 추가적으로 생각할 시간이 더 필요하다는 설명이었다. 여기서 추가한 Feed-Forward Network은 이렇게 토큰별로 심도있는 처리를 담당한다.
Residual Connections
이 Attention을 활용한 transformer 아키텍처의 문제점은 deep하다는 것이다. 심층 신경망(Deep Neural Network, DNN)의 단점 중 하나는 모델이 깊어질수록 기울기 소실(vanishing gradient)와 기울기 폭발(exploding gradient) 등의 문제로 인해 학습이 어려워진다는 점이다. 네트워크들이 주로 곱셈으로 이루어져있기에 어찌보면 당연한 현상이다. $0.1 \times 0.1 \times \cdots$ 혹은 $1.1 \times 1.1 \times \cdots$ 와 같은 일이 발생하면 기하급수적으로 값이 변하는 것은 당연하기 때문이다. 게다가 activation function을 적용하면 극단적인 값들의 기울기는 0에 가까운 값으로 변할 수 있으므로 기울기 소실이 잘 발생할 수 있다.
이런 현상을 최소화하기 위해 ResNets(Residual Connection, Skip Connections)이 transformer에도 적용되었다. (He et al. 2016) Transformer 아키텍처는 여러 개의 attention block이 연결되어 이루어져있는데, 각 블록을 전부 연결하는 것이 아니라 중간 중간 건너뛰어서 계산하기도 한다.
Layer Normalization
Transformer 학습의 안정화를 위해 적용한 또 다른 방법은 layer normalization이다. (Ba, Kiros, and Hinton 2016) 이 방법은 batch normalization과 유사하지만, 대상을 batch가 아닌 layer에 적용했다.
각 레이어마다 나온 출력값들을 일정한 분포가 유지되도록 조정해서 activation function이 적용되어도 기울기 소실(vanishing gradient) 등의 문제가 발생하지 않도록 도와준다. 이를 어려운 말로 학습 과정에서의 내부 공변량 변화(internal covariate shift) 문제를 줄이기 위해 정규화(regularization)한다고 표현한다. Layer normalization은 레이어마다 적용하는 것이기 때문에 배치 사이즈과는 무관하고, 깊은 네트워크일수록 유리하다.
Dropout
심층 신경망의 또다른 문제점은 과적합(overfitting)으로 인해 일반화 성능(generalization)이 떨어진다는 점이다. 이 현상의 원인 중 하나는 파라미터 수가 매우 많아서 훈련 데이터에 대해서 과도하게 학습될 가능성이 있기 때문이다. 이를 해결하기 위해 나온 방법 중 하나가 (Srivastava et al. 2014)에서 나온 Dropout이다.
이 방법은 굉장히 심플한데 훈련(training)할 때 그냥 랜덤하게 일부 뉴런(neuron)을 비활성화 시켜서 학습하고 추론(inference)시에는 모든 뉴론을 활성화시킨 네트워크를 사용한다. 이렇게 하면 모델이 특정 뉴런이나 특정 뉴런 조합에 과도하게 의존하는 것을 방지할 수 있다. 또한 랜덤으로 비활성화 시킨 네트워크를 각각 다른 네트워크처럼 생각하면 앙상블(ensemble) 모델 학습시키는 것과 같은 방식이라고 간주할 수도 있다.
Conclusion
지금까지 어텐션 매커니즘에 대해서 알아보았다. 이 글을 쓴 2024년에도 딥러닝에 있어서 가장 중요한 알고리즘 중 하나라고 할 수 있겠다. 또한 transformer 자체가 워낙 무겁기 때문에 이를 경량화하기 위한 여러 방법들은 이 어텐션 매커니즘을 최적화하는 방법들이 많고, 다양한 논문들이 transformer의 근본을 건드리거나 개선하려고 노력하고 있다. 그러기에 2024년에도 Back to Basics의 관점으로 다시 한번 복습하기 위해 이 포스트를 작성하였다. 아쉬운 건 Decoder입장에서만 작성했고, Encoder와의 차이점, 그리고 Cross Attention 부분도 넣었어야 했으나 너무 지쳐서 포기했다. 다른 자료에 설명이 잘 되어있으니 참고하면 되겠다.
참고로 Let’s build GPT뿐만 아니라 여러가지 다른 좋은 포스트와 책, 글들이 많기에 기록하고자 한다. (다만 다 영어다.)
- The Illustrated Transformer
- Tweets from @akshay_pachaar
- Getting Meaning from Text: Self-attention Step-by-step Video
- Understanding and Coding the Self-Attention Mechanism of Large Language Models From Scratch
- 현재 이 내용은 Build a Large Language Model (From Scratch)라는 책으로 쓰여지고 있다. (Livebook)
- Illustrated Guide to Transformers Neural Network: A step by step explanatio
-
[Visualizing Attention, a Transformer’s Heart Chapter 6, Deep Learning](https://www.youtube.com/watch?v=eMlx5fFNoYc)
Reference
- Vaswani, Ashish, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N Gomez, Łukasz Kaiser, and Illia Polosukhin. 2017. “Attention Is All You Need.” Advances in Neural Information Processing Systems 30. https://arxiv.org/abs/1706.03762.
- Bengio, Yoshua, Réjean Ducharme, and Pascal Vincent. 2000. “A Neural Probabilistic Language Model.” Advances in Neural Information Processing Systems 13. https://dl.acm.org/doi/10.5555/944919.944966.
- Bahdanau, Dzmitry, Kyunghyun Cho, and Yoshua Bengio. 2014. “Neural Machine Translation by Jointly Learning to Align and Translate.” ArXiv Preprint ArXiv:1409.0473. https://arxiv.org/abs/1409.0473.
- Sutskever, Ilya, Oriol Vinyals, and Quoc V Le. 2014. “Sequence to Sequence Learning with Neural Networks.” Advances in Neural Information Processing Systems 27. https://arxiv.org/abs/1409.3215.
- He, Kaiming, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. 2016. “Deep Residual Learning for Image Recognition.” In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 770–78.
- Ba, Jimmy Lei, Jamie Ryan Kiros, and Geoffrey E Hinton. 2016. “Layer Normalization.” ArXiv Preprint ArXiv:1607.06450.
- Srivastava, Nitish, Geoffrey Hinton, Alex Krizhevsky, Ilya Sutskever, and Ruslan Salakhutdinov. 2014. “Dropout: a Simple Way to Prevent Neural Networks from Overfitting.” The Journal of Machine Learning Research 15 (1): 1929–58.