Logit, Sigmoid, Softmax, and Cross-Entropy
Introduction
개인적으로 정리도 할 겸 그리고 다른 포스트에서 이 부분을 설명할 때 글이 너무 길어져서 분리해서 작성하는 포스트이다. 최대한 직관적으로 적어보려고 노력하였다.
logit
도박을 생각해보자. odds란 도박의 승률을 나타내는 중요한 지표이다. 확률이 이길 확률($p$)과, 전체 경우의 수(이김 + 짐)의 합(1)으로 $\dfrac{p}{(p + (1-p))} = \dfrac{p}{1} = p$ 표시되는 형태라면, odds는 이길 확률($p$)과 질 확률($1-p$)의 비율로 표시된다. odds는 이길 확률이 질 확률에 비해 몇 배냐 더 큰 것인가?라는 것을 표현하는 지표이다.
\[\begin{equation} \textrm{odds} = \dfrac{p}{1-p} \end{equation}\]참고로 왜 확률이 아니라 odds를 쓰냐고 하면, odds가 계산이 쉽기 때문이다. odds의 표기법은 여러가지가 있는데, British Odds($(1-p)/p$)로 표현할 때, odds가 $ 32/7 $ 이라고 하자. 확률로 계산하면 승리확률이 $ \dfrac{7}{32+7} = 0.17 $이고, 여기에 배당금까지 계산하려면 복잡하다. 하지만 odds 계산으로는 7만원을 걸면 32만원을 딸 수 있다고 계산할 수 있다. (이기면 39만원 보유)
다시 돌아와서 odds에 로그를 취한 것을 log odds이라고 하고 이를 확장하여 함수의 형태로 표현하면 logistic unit, 줄여서 logit 라고 한다. 로그를 취한 이유는 일종의 트릭이라고 볼 수 있는데, 로그를 취하면 함수의 특성 (증가,감소나 극점의 유지)을 유지시키면서도 복잡한 곱셈이나 나눗셈 연산을 덧셈과 뺄셈으로 바꿀 수 있기에 계산의 편의성을 위해 사용한다고 보면 된다.
\[\begin{equation} \textrm{logit}(x) := \ln{\dfrac{x}{1-x}} \end{equation}\]logit이 log odds에서 출발하기는 했지만, 일반적으로는 모델을 통해 나온 출력값을 뜻한다. 예를 들면 어떤 모델을 통해 count값이 나왔다고 가정했을 때, logit은 그 count값이 될 수 있다. 하지만, 이러면 확률로 변환이 안 되어있어 계산하기가 번거롭기에 확률로 바꿔주는 도구가 필요하다.
sigmoid
그러면 logit함수를 다시 확률로 바꾸려면 어떻게 해야할까? 위에서 logit함수를 정의했고, 이는 확률(p)로부터 정의되기 때문에, 다음과 같이 위의 logit함수의 역함수(inverse function)을 취하면 확률을 다시 구할 수 있다.
\[\begin{align*} x &= \textrm{logit}(y) \equiv \ln{\dfrac{y}{1-y}} \\ e^x &= \dfrac{y}{1-y} \\ (1-y) e^x &= y \\ e^x &= y (1 + e^x) \\ y &= \dfrac{e^x}{1+e^x} = \dfrac{1}{1+e^{-x}} \end{align*}\]그리고 이 함수를 sigmoid 함수라고 한다.
\[\begin{equation} \textrm{sigmoid}(x) := \dfrac{1}{1+e^{-x}} \end{equation}\]
sigmoid 함수를 통해 어떤 값 logit을($-\infty, \infty$) 확률의 범위인 ${0, 1}$사이로 한정(clamping) 혹은 압축할 수 있다. 그래서 sigmoid를 logitstic function이라고 하기도 한다.
softmax
앞에서 본 sigmoid는 2개 (Win/Loss)의 클래스에 대해 분류하는 문제에 적용할 수 있는 문제이다. 이를 K개의 클래스로 확장하면, softmax 함수가 된다.
\[\begin{align} \textrm{softmax}(x_i) &:= \dfrac{e^{x_i}}{\sum_{j=1}^K e^{x_j}} \\ \end{align}\]logit과 sigmoid 입장에서 softmax를 해석하면, 단순하게 odds로 바꾸어서 생각하면 된다. 어떤 logit(log odds) $X$가 있을 때, 지수 함수(exponential function)를 취하면 $\textrm{odds} \in [0, +\infty)$ 형태가 된다.
\[\begin{align*} e^x = e^{\log{\textrm{odds}}} = \textrm{odds} \end{align*}\]이를 확률로 만들기 위해 분모는 다 더하고 (모든 클래스의 확률의 합은 1), 분자는 하나의 odds만 남기면 된다.
\[\begin{align*} \textrm{softmax} = \dfrac{\textrm{Single odds}}{\textrm{Sum of odds}} = \dfrac{e^{x_i}}{\sum_{j=1}^K e^{x_j}} \end{align*}\]참고로 다시 역으로 softmax로부터 sigmoid로 유도하면 다음과 같다. (어떤 binary classification output $x$를 $x = x_0 - x_1$이라고 정의)
\[\begin{align*} \textrm{sigmoid} = \dfrac{e^{x_0}}{e^{x_0} + e^{x_1}} = \dfrac{1}{1 + \dfrac{e^{x_1}}{e^{x_0}}} = \dfrac{1}{1 + e^{x_1-x_0}} = \dfrac{1}{1 + e^{-(x_0 - x_1)}} = \dfrac{1}{1 + e^{-x}} \end{align*}\]Multinomial Logistic Regression (Softmax Regression)
softmax는 다중 분류 문제(MultiClass Classification Problem)에 사용된다. 이 떄 사용하는 방법을 다항 로지스틱 회귀(Multinomial Logistic Regression)이라고 한다.
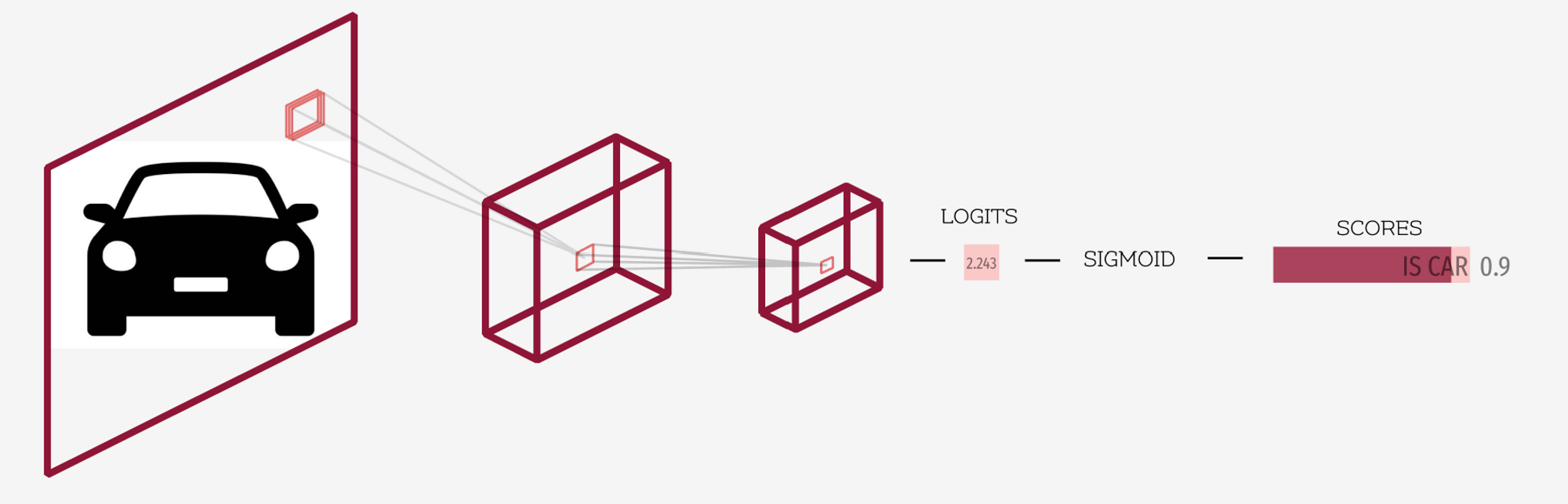
이진 분류(Binary Classification)에서는 단순히 Yes/No로 판별할 확률만 알면 됐다. 아래 그림처럼 logits를 sigmoid함수에 통과시켜 확률을 얻은 뒤, 확률에 따라 자동차인지 아닌지 분류하면 되는 문제였다.
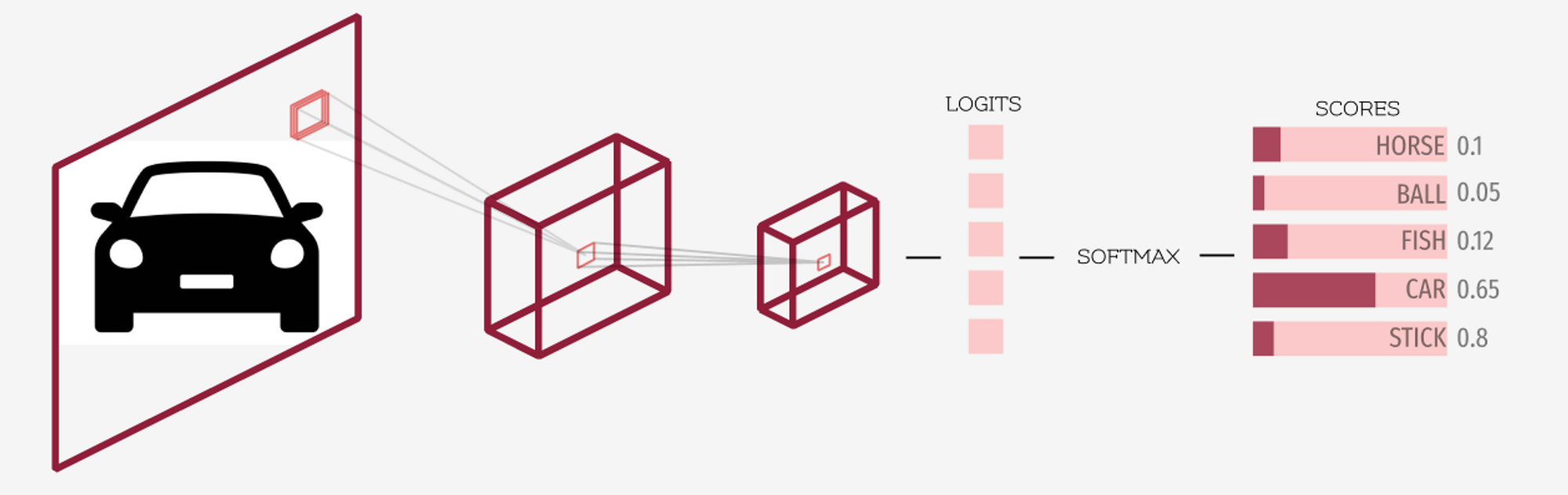
그러나, 다중 분류 문제에서는 logits를 softmax에 통과시켜 각 클래스에 속할 확률을 구한 뒤, 가장 높은 확률의 클래스를 선택하는 문제로 변화하게 된다. 이런 문제를 Multinomial Logistic Regression 혹은 softmax regression이라고 한다.
Cross Entropy Loss
그러면 이런건 어떻게 학습시켜야할까? 일반적인 확률적 경사하강법(SGD, Stochastic Gradient Descent)에서는 loss function $\mathcal{L}$을 정의하고 loss function을 통해 정답과 출력의 차이를 최대한 좁히도록 모델 파라미터를 업데이트하는 방식을 취한다.
지도 학습(Supervised Learning) 분류 문제에서 출력(output)을 $\hat{y}$, 그리고 대상 혹은 정답(target)을 $y$이라고 지정하면, loss function $\mathcal{L}$은 다음과 같이 정의할 수 있다.
\[\begin{equation} \mathcal{L}(\hat{y}, y) = \textrm{A difference between } \hat{y} \textrm{ and } y \end{equation}\]하지만 처음부터 다중 분류(Multiclass)로 접근하면 복잡하니까 단순하게 이진분류(Binary Classification)으로 돌아가보자.
어떤 모델 $f$가 파라미터 $\theta$에 의존한다고 했을때 입력 $x$에 대해 정의되는 모델의 logit을 $f_\theta(x)$이라고 정의할 수 있다. 이를 확률로 바꾸면 $\textrm{sigmoid}(f_\theta(x))$라고 할 수 있고, 이 때 sigmoid를 $\sigma$로 표현하기도 한다. 해당 파라미터 $\theta$와 데이터 인덱스 $i$에 대한 입력과 출력을 $x_i$과 $\hat{y}_{\theta, i}$라고 표현하면 이 내용을 다음과 같은 식으로 표현이 가능하다.
\[\begin{equation} \hat{y}_{\theta, i} = \sigma \left( f_\theta(x_i) \right) \end{equation}\]Likelihood
이 모델을 어떻게 훈련한다는 것은 어떤 의미일까? 모델 훈련은 loss function을 최소화화여, 모델의 예측이 실제 클래스(혹은 레이블)에 가장 가깝도록하는 것이다. loss function은 얼마나 모델이 잘못되었는지 알려주는 함수인데, 모델이 정확할 수록 모델의 잘못됨은 작아질 수 밖에 없다.
따라서 모델을 효과적으로 훈련시키기 위해서는, 훈련 데이터가 어떤 확률 분포를 따르고 있는지를 파악하는 것이 중요하다.
이전의 접근 방식에서 우리는 모델이 정답 클래스를 예측할 확률에 초점을 맞췄다. (분류문제라고 했을 때) 하지만, 이는 본질적으로 모델의 매개변수가 주어진 훈련 데이터에 얼마나 잘 맞는지를 측정하는 것과 관련이 있다. 여기서 얘기하는 얼마나 잘 맞는지에 대한 적합도, 즉 데이터가 특정 모델 매개변수를 얼마나 ‘지지’하거나 ‘가능하게 하는지’의 척도를 가능도(likelihood)라고 한다. 우도라고 표현하는 경우도 있지만, 가능도 혹은 기여도라고 해석하는게 직관적이다. 영어로 보면 “Like”란 단어는 좋아하다라는 의미도 있지만 ‘가깝다’, ‘유사함’의 의미로 생각하면 이해가 쉬울 것이라고 생각한다.
처음에 이해하기 어려운 개념이다. 그러나, 알고보면 그동안 사람들이 매번 하는 것이다.
예를 들어 소개팅을 나간다고 하자, 소개팅에서 연애로 발전할 확률을 구할 수도 있다. 이는 특정 분포 (그동안 경험을 통해 보유)를 통해 새로운 소개팅 이성에 대해 성공할 확률을 계산할 수 있다. 이는 분포로부터 데이터를 추정이라고 볼 수 있다. 즉, 확률(Probability)이다. (분포 고정)
반대로 상대방 이성에 대한 정보(데이터)가 소개팅 성공에 얼마나 기여할까를 측정할 수도 있다. 프로필사진을 더 신뢰할 수도 있고, 주변인들의 전언을 더 신뢰할 수도 있다. (모델 파라미터) 경험이 쌓일수록 내가 어떤 정보를 더 신뢰해야하는가에 대해 통찰력이 생길것이다. 이는 데이터로부터 분포를 추정이라고 볼 수 있다. 즉, 가능도(Likelihood)이다. (데이터 고정)
이를 수식으로 얘기하면 각각 조건부확률(Conditional Probability)를 이용하여 분포를 포현하는 모델 파라미터 $\theta$와 데이터 $x$에 대해 다음과 같이 정의할 수 있다.
\[\begin{align} \textrm{Probability} & := P(X | \theta) \; (\textrm{fixed } \theta) \\ \textrm{Likelihood} & := L(\theta | x) = P(X=x | \theta) \; (\textrm{fixed } X) \\ \end{align}\]MLE(Maximum Likelihood Estimation) and Log-likelihood
그러면 모델은 주어진 데이터를 통해 확률분포를 예측하는 걸 훈련하는게 목적이라고 정의한다고 했다. 즉, 가능도를 최대화 해야한다. (Maximize Likelihood)
그리고 가능도를 최대화하도록 모델 파라미터를 추정하는 것을 MLE(Maximum Likelihood Estimation)이라고 한다.
MLE를 어떻게 쉽게 할 수 있을까? 그건 위에서도 사용한 로그를 이용하면 된다. 곱셈이 덧셈으로 바뀌어서 계산이 쉬워지기 때문이다.
아까의 예시를 이어서 들면, 전혀 모르는 사람들과 지속적으로 소개팅을 한다면 각각은 독립적인 사건이라고 볼 수 있다. 물론 소개팅이 안돼서 심리적으로 위축돼서 더 잘 안될수도 있겠지만, 강철멘탈이라고 가정하자.
수학에서 독립 시행의 확률은 곱셈으로 정의된다.
\[\begin{align} P(A \cap B) = P(A) P(B) \end{align}\]logit에서처럼 곱셈보다는 덧셈이 계산하기가 훨씬 편하다. 따라서, 확률도 Log를 씌워보자.
\[\begin{align} \log{P(A \cap B)} = \log{P(A)} + \log{P(B)} \end{align}\]가능도(Likelihood)도 마찬가지이다. 새로운 데이터가 들어올때마다 곱셈보다 지속적으로 더해줄 수 있는 형태를 만드는게 좋다.
\[\begin{align} \log{L(A \cap B)} = \log{L(A)} + \log{L(B)} \end{align}\]이렇게 로그를 씌운 형태를 로그 가능도(log-likelihood)라고 한다.
그러면 MLE의 곱셈은 로그 가능도(log-likelihood)를 이용하면 덧셈으로 변경된다.
\[\begin{align} L(\theta | x) = P(X=x | \theta) &= \prod_{k=1}^n P(x_k | \theta) \\ \log{L(\theta | x)} = \log{P(X=x | \theta)} &= \sum_{k=1}^n \log{P(x_k | \theta)} \end{align}\]Back to Binary Classification
만약, 입력 $x$에 대해서 출력 $Y$ (0 or 1)를 만들때 그 출력을 다음과 같이 표현해보자. $x$랑 $Y$ 모두 데이터이고, 모델 파라미터 $\theta$가 주어졌을 때의 $x$에 대한 확률 $p$를 표현하기 위해 ;을 사용했다.
\[\begin{align} P(Y=1 | X=x) = p(x; \theta) \end{align}\]조건부 가능도(Conditional Likelihood)는 다음과 같이 표현가능하다.
\[\begin{equation} L(\theta | y) = \prod_{i=1}^n P( Y = y_i | X = x_i) = \prod_{i=1}^n \hat{y}_{\theta,i}^y (1-\hat{y}_{\theta,i})^{1-y} \end{equation}\]이 중에서
\[\begin{align*} \hat{y}_{\theta,i}^y (1-\hat{y}_{\theta,i})^{1-y} = \begin{cases} \hat{y}_{\theta,i}^y \; &\textrm{ where } y == 1 \\ (1-\hat{y}_{\theta,i}) \; &\textrm{ where } y == 0 \\ \end{cases} \end{align*}\]이 식은 이항분포(Bernoulli distribution) 확률밀도 함수에서 가져온 식인데, 각 $y$에 따라 동작을 달리한다.
이 조건부 가능도(conditional likelihood)를 최대화 하기 위해 로그를 사용하면
\[\begin{align} \log{L(\theta | y)} &= \sum_{i=1}^n \log{P( Y = y_i | X = x_i)} \\ &= \sum_{i=1}^n \log{\hat{y}_{\theta,i}^{y_i} (1-\hat{y}_{\theta,i})^{1-y_i}} \\ &= \sum_{i=1}^n \log{\hat{y}_{\theta,i}^{y_i}} + \sum_{i=1}^n \log{(1-\hat{y_i}_{\theta,i})^{1-y_i}} \\ &= \sum_{i=1}^n y_i\log{\hat{y}_{\theta,i}} + \sum_{i=1}^n (1-y_i)\log{(1-\hat{y}_{\theta,i})} \end{align}\]하지만 loss function입장에서는 최소화를 하는것을 지향하기 때문에 $-$를 붙여서 Negative Log-likehood(NLL)를 최소화하는 문제로 바꿔준다.
따라서 이진 분류(Binary Classification) 문제의 목적은 가능도를 최대화 하는것이 목적이며, 이는 loss function $\mathcal{L}$은 $n$개의 레이블에 대해서 Negative Log-likelihood, $-\log{L}$을 최소화하는 것과 같다.
\[\begin{equation} \mathcal{L}(y, \hat{y}) = -\sum_{i=1}^n y_i\log{\hat{y}_{\theta,i}} - \sum_{i=1}^n (1-y_i)\log{(1-\hat{y}_{\theta,i})} \end{equation}\]여기서 $\theta$를 생략하고 $n$개의 데이터에 대해 평균을 내면 다음과 같이 정리할 수 있다.
\[\begin{equation} \mathcal{L}(y, \hat{y}) = - \dfrac{1}{n} \sum_{i=1}^n \left[ y_i\log{\hat{y}_{i}} + (1-y_i)\log{(1-\hat{y}_{i})} \right] \end{equation}\]이 때 예측 확률 $\hat{y}$는 sigmoid 함수를 사용하여 표현할 수 있다.
\[\begin{align} \textrm{sigmoid}(z) = \sigma(z) &= \dfrac{1}{1 + e^{-z}} \\ \hat{y} &= \sigma(f_\theta(x)) \end{align}\]Extend to Multiclass Classification
이를 다중 클래스로 확장하면 원래 목적이었던 Cross Entropy Loss를 구할 수 있다.
sigmoid 에서 softmax로 확장한것처럼 이진 분류(Binary Classification)의 Negative Log-likelihood을 Mutli-Class Classification의 Cross Entropy Loss로 확장할 수 있다.
\[\begin{align} \textrm{sigmoid}(z) &= \dfrac{1}{1+e^{-z}} \\ \textrm{softmax}(z_i) &= \dfrac{e^{z_i}}{\sum_{j=1}^K e^{z_j}} \end{align}\]우선 이진 분류의 loss function을 데이터 한 개에 대해 표현하면 다음과 같다. ($i$는 그래서 생략) 이 떄 $c$는 클래스(class) 혹은 레이블의 약자 c이다.
\[\begin{align} \textrm{sigmoid}(z) &= \dfrac{1}{1+e^{-z}} \\ \hat{y} &= \textrm{sigmoid}(f_\theta(x)) \\ \mathcal{L}(y, \hat{y}) &= -y\log{\hat{y}}- (1-y)\log{(1-\hat{y})} \\ &= - \sum_{c=1}^2 y_c \log{\hat{y}_{c}} \end{align}\]맨 밑줄은 일반적인 표기법은 아니지만, 다중 분류로의 확장을 위해 표기법을 변경하였다. 이진 분류에서 1번과 2번 클래스를 다음과 같이 정의하고 \(y^1 = y\), \(y^2 = 1-y\), 확률도 \(\log{\hat{y}_\theta^1} = \log{\hat{y}}\), \(\log{\hat{y}_\theta^2} = 1-\log{\hat{y}}\) 이렇게 표현할 수 있기 때문에 $\sum$으로 묶어서 표현할 수 있다.
이런 구조는 $\textrm{레이블} \times \textrm{레이블의 확률}$의 합의 형태를 띈다.
그러면 이 구조를 유지하면서 다중 분류를 위해 2개의 class를 $K$개의 class로 확장하면, 다음과 같이 확장할 수 있게 된다. 표기법을 살짝 변경했는데, 위첨자(superscript)를 표현하던 클래스를
\[\begin{align} \mathcal{L}(y, \hat{y}) &= - \sum_{k=1}^K y_k \log{\hat{y}_{k}} \end{align}\]위에서 다중 분류 문제에서 레이블의 확률을 구할 때 sigmoid대신 softmax를 사용한다고 했으므로
\[\begin{align} \textrm{softmax}(z_i) &= \dfrac{e^{z_i}}{\sum_{j=1}^K e^{z_j}} \\ \hat{y} &= \textrm{softmax}(f_\theta(x)) \\ \mathcal{L}(y, \hat{y}) &= - \sum_{k=1}^K y_k \log{\hat{y}_k} \end{align}\]그럼 다음과 같이 모델 \(\hat{y}_{\theta, i} = \textrm{softmax} \left( f_\theta(x_i) \right)\)와 정답 클래스 c에 대해 Cross Entropy Loss를 유도해보도록 하자.
위의 loss function은 실제 클래스 $c$에 대해서만 $y_c=1$이기 때문에 나머지 $y_k = 0 \textrm{ where } k \neq c$이다. 따라서, $\sum_{k=1}^K$은 없어지고 $\log{\hat{y}_c}$ 만 남게 된다.
\[\begin{align} \mathcal{L}(y, \hat{y}) &= - \sum_{k=1}^K y_k \log{\hat{y}_k} \\ &= -\log{\hat{y}_c} \end{align}\]여기서 softmax함수의 정의를 $\hat{y}_c$에 대입하면 Cross Entropy Loss는 다음만 남게 된다.
\[\begin{equation} \mathcal{L}(y, \hat{y}) = -\log{\dfrac{\exp{f_\theta(x_c)}}{\sum_{k=1}^K \exp{f_\theta(x_k)}}} \end{equation}\]Information Theory
그러면 왜 Cross Entropy라고 불리울까? 엔트로피는 무질서도 아니었나? 크로스 엔트로피는 또 무슨 말일까? 이 부분을 좀 더 깊게 설명해보고자 한다. 쉽게 이해하기 어려운 개념이나 이 블로그 글과 HORIZON에 연재된 글이 이해에 많은 도움을 주었고, 이를 정리해보고자 한다. 같이 읽어보는 걸 추천한다.
Information
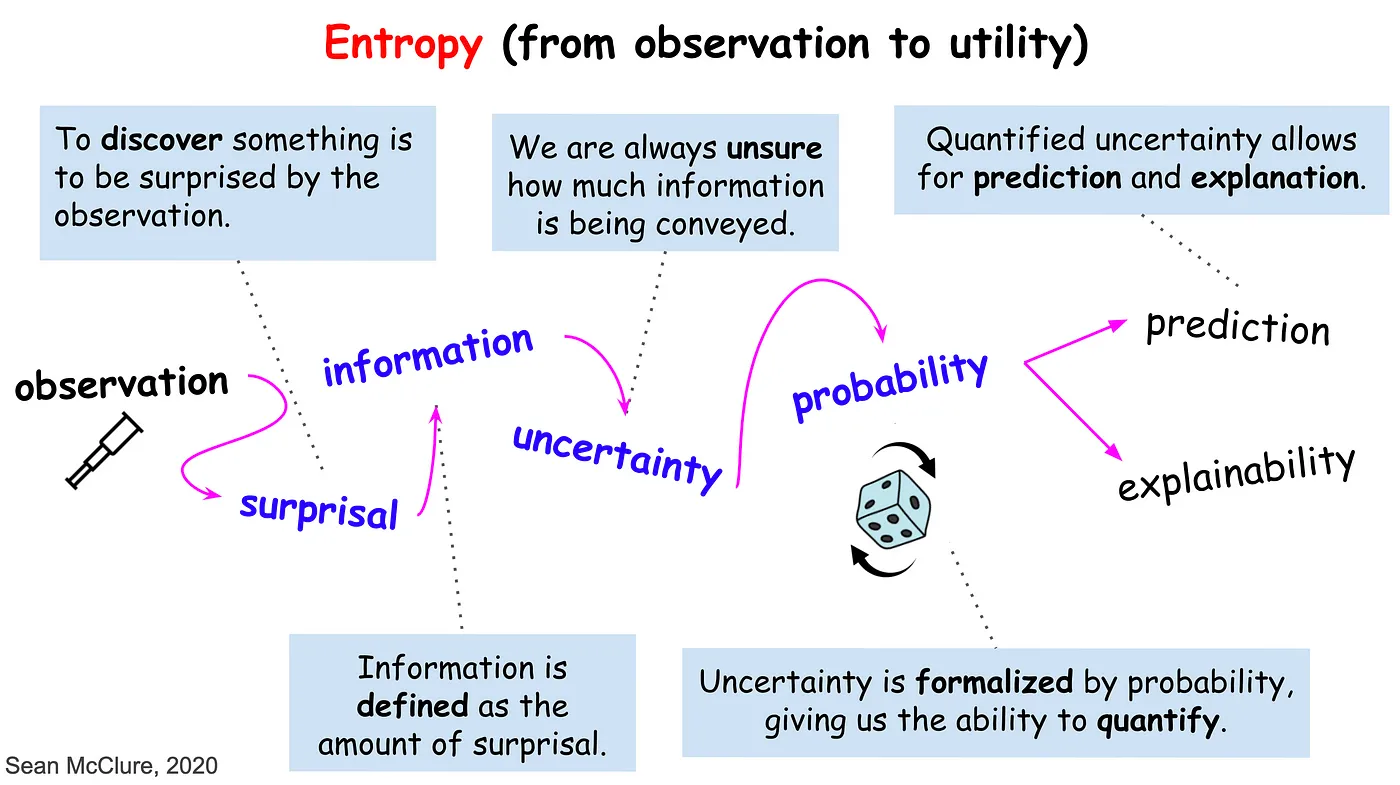
사람은 항상 관찰하고 발견한다. 하지만, 둘은 같은 개념이 아니다. 발견은 관찰로부터 이루어진다. 평소와 다른 무엇인가를 관찰했을 때 이를 발견이라고 할 수 있다. 정보는 얼만큼 평소와 다른가, 즉 놀람의 정도(surprisal)에 의해 정의될 수 있다. 하지만 놀람이란 감정적인 단어다. 과학적으로 해석하기 위해 이 놀람의 정도를 정량화하면 불확실성(Uncertainty)이 된다. 그리고, 그 불확실성은 확률(Probability)에 의해 측정된다. 낮은 확률의 사건은 불확실성이 높은 사건이고 이는 많은 정보량을 얻을 수 있다. 이렇게 확률로 측정되어지는 정량화된 불확실성은 우리에게 예측(prediction)과 설명(explainability)을 제공해준다.
자 이제 수학적으로 어떻게 접근해볼지 생각해보자.
he fundamental problem of communication is that of reproducing at one point either exactly or approximately a message selected at another point
(Shannon 1948)
(Claude Shannon, 1948)
정보 과학을 설명하면 클로드 섀논이 빠질 수 없고, 섀논이 쓴 정보과학의 시작인 이 논문에 (Shannon 1948) 등장하는 문장이다. 여기서 언급한대로 통신, 정보의 전달, 혹은 커뮤니케이션은 정보를 그대로 재현하거나, 아니면 다른 지점으로 옮겨서 대략적으로 재현하는 것에서 시작한다. 이 때, 메시지는 가능한 메시지의 집합으로부터 추출된 것을 의미한다.
말이 어렵다고 느껴지는가? 지금 설명하고 있는 “한국어”도 이 엔트로피란 개념을 전달하기 위한 메시지에 불과하다. 한국어 단어의 집합에서 추상적인 개념인 엔트로피를 설명하기 위해 필요한 단어들을 추출해서 전달한다고 보면 되는 것이다. 이 때 강의 전달력이 좋은 사람이라면 개념의 손실을 줄이고 제대로 설명할 수 있겠지만, 그렇지 않다면 뭐라고 설명하는지 알아듣기 힘들 것이다. 즉, 정보의 전달과정에서 일종의 압축이 필요하고, 그 와중에서 손실은 피할 수 없는 문제이다.
수학적으로는 분포 $P$에서 메시지들 혹은 기호의 집합 $X_n$을 랜덤 추출한 것을 메시지라고 할 수 있다. 이걸 정량화하려면 어떻게 생각해야할까? 섀년은 이 $X_n$에 로그를 취하는 방식을 택했다. 섀년 시대의 펀치카드를 예를 들면 직관적으로 펀치카드를 하나 쓸 때 보다 2개 쓸때 전달할 수 있는 메시지량이 2배가 되며, 채널이 하나에서 2개로 될 때 전송하는 메시지량이 는다고 생각할 수 있었다. 그리고 위에서 언급했던 것처럼 로그를 취하면 수학적으로 다루기 쉬워지는 경향이 있다.
수학적으로는 특정 사건 혹은 메시지의 정보량(Shannon Information)은 다음과 같이 로그로 표현한다. 보통 $b=2$로 두고 bit로 표현한다.
\[\begin{equation} h(x) := -\log_b \dfrac{1}{P(x)} = -\log_2 {P(x)} \end{equation}\]Entropy
하지만 특정 사건이 아니라 전체 사건에서의 종합적인 정보량은 어떻게 정량화 해야할까? 이럴 때 쓰는 것이 엔트로피(Entropy)이다.
엔트로피(entropy)는 데이터 압축 (source coding) 한계를 제공해준다. 우리가 보통 쓰는 bit(0 or 1)위주의 엔트로피를 가정하면, 3비트는 최대 $8(2^3$)가지의 경우의 수를 제공하며, 이는 3비트는 데이터를 8가지 경우의 수로 압축할 수 있다는 것을 뜻한다. 위 문단에서는 사건 하나 즉, \(\dfrac{1}{8}\)의 사건 하나에 대한 정보량을 표현했다면 엔트로피를 이용하면 전체 경우의 수 (8가지)에 대해 이야기할 수 있다.
이를 5비트로 확장해보자. 5비트는 최대 $2^5$ 즉 32가지의 경우의 수를 제공한다. 이 중 어떤 사건이 발생했다면 \(\dfrac{1}{32}\)의 확률이라고 할 수 있다. 앞에서의 3비트에서는 \(\dfrac{1}{8}\)였으므로 이때보다 작은 확률을 보여준다.
이렇게 각각의 정보량을 종합하면 엔트로피가 되는데, 엔트로피(entropy)는 랜덤 변수 $X$에 대해서 모든 사건($\mathcal{A}_X$)에 대한 정보량(Shannon Information)의 기대값, 혹은 평균 정보량이라고 할 수 있다.
\[\begin{align} H(X) &\equiv \sum_{x \in \mathcal{A}_X } P(x) \log{\dfrac{1}{P(x)}} \\ &= \mathbb{E}_X \log{P(\mathbf{X})} \end{align}\]이 때 사건이 일어날 확률이 0이면 어떻게 해야할까? $P(x) = 0$이면 로그는 음의 무한대로 발산하게 된다. 하지만 일어나지 않는 사건은 아무 의미가 없다. 따라서 $P(x) = 0$일 때는 엔트로피 계산에서 제외된다.
엔트로피에는 다음과 같은 성질이 존재한다.
- $P(x) = 1$에 가까워지면, 즉 사건이 결정적(deterministic)하면, 엔트로피는 낮아진다. 놀람의 정도가 낮다고 해석할 수 있다.
- $H(X)$를 최대화하는 방법은, 모든 사건이 균등(uniform)한 확률을 가질 때이다. 모두 균등한 확률을 가질 때 놀람의 정도는 최대라고 할 수 있다. 이를 수학적으로는 다음과 같이 표현한다.
\(\begin{equation} H(X) \leq \log{|\mathcal{A}_X|} \end{equation}\) 을 만족하고, 각 사건의 확률이 동일할 때, 수학적으로 $P_i (x) = 1 / |\mathcal{A}_X|$ (Uniform probability) 일 때 등호를 만족한다.
Joint Entropy
엔트로피는 어떤 랜덤 변수 $\mathbf{X}$에 대한 정보량의 기대값이라고 하였다. 이를 확장하여 두 랜덤 변수 $\mathbf{X}$와 $\mathbf{Y}$에 대해서는 어떻게 해야할까?
만약 독립적인 두 랜덤 변수 $\mathbf{X}$와 $\mathbf{Y}$가 있다면 다음을 만족한다.
\[\begin{equation} H(\mathbf{X, Y}) = H(\mathbf{X}) + H(\mathbf{Y}) \end{equation}\]증명은 로그의 성질을 응용하면 쉽다.
\[\begin{align*} H(\mathbf{X, Y}) &= -\sum_{(x, y) \in \mathbf{XY}} P(x,y) \log{P(x,y)} \\ &= -\sum_x \sum_y P(x) P(y) \log{\left(P(x) P(y)\right)} \\ &= -\sum_x \sum_y \left( P(x) \log{P(x)} \right) P(y) - \sum_x \sum_y \left( P(y) \log{P(y)} \right) P(x) \\ &= -\sum_x P(x) \log{P(x)} \sum_y P(y) - \sum_y P(y) \log{P(y)} \sum_x P(x) \\ &= -\sum_x P(x) \log{P(x)} \cdot 1 - \sum_y P(y) \log{P(y)} \cdot 1 \\ &= -\sum_x P(x) \log{P(x)} - \sum_y P(y) \log{P(y)} \\ &= H(\mathbf{X}) + H(\mathbf{Y}) \end{align*}\]Conditional Entropy
조건부 확률처럼 조건부 엔트로피도 정의할 수 있다. 이는 랜덤 변수 $\mathbf{X}$ 가 주어졌을 때, 다른 랜덤 변수 $\mathbf{Y}$의 불확실성을 측정할 때 사용한다.
\[\begin{align*} H(\mathbf{Y} | \mathbf{X}) &\equiv \mathbb{E}_{P(\mathbf{X})} \left[ H(P(Y|X))\right] \\ &= \sum_x P(x) H(P(Y|X =x)) = -\sum_x P(x) \sum_y P(y|x) \log{P(y|x)} \\ &= -\sum_{x,y} P(x,y) \log{P(y|x)} = -\sum_{x,y} P(x,y) \log{\dfrac{P(x,y)}{P(x)}} \\ &= -\sum_{x,y} P(x,y) \log{P(x,y)} - \sum_{x} P(x) \log{\dfrac{1}{P(x)}} \\ &= H(X, Y) - H(X) \end{align*}\]Mutual Information
하지만 만약 독립적인 변수가 아니라면 어떻게 될까? Joint Entropy에서는 독립 랜덤 변수 $\mathbf{X}$와 $\mathbf{Y}$에 대해 다루었다면, 이번에는 종속적인 변수를 다뤄보고자 한다.
$\mathbf{X}$와 $\mathbf{Y}$가 서로 종속적이라면 둘이 공유하는 정보가 있을 것이고 이를 mutual information이라고 정의한다.
\[\begin{equation} I(\mathbf{X}; \mathbf{Y}) = H(\mathbf{X}) + H(\mathbf{Y}) - H(\mathbf{X, Y}) \end{equation}\]이는 다음과 같이 유도될 수 있다.
\[\begin{align*} I(\mathbf{X}; \mathbf{Y}) &= \sum_{x,y} P (x,y) \left( \log{\dfrac{P (x,y)}{P(x) P(y)}} \right) \\ &= \sum_{x,y} \left( P (x,y) \log{P (x,y)} - P (x,y) \log{P(x)} - P (x,y) \log{P(y)} \right) \\ &= - H(X, Y) + H(X) + H(Y) \\ &= H(X) + H(Y)- H(X, Y) \\ &= H(X) - H(X | Y) \\ &= H(Y) - H(Y | X) \\ \end{align*}\]mutual information의 정의를 변형하면 joint entropy를 설명할 때 가정한 독립 변수 조건을 확장할 수 있다. joint entropy를 합집합(union), mutual information을 교집합(intersection)이라고 생각하면 된다.
\[\begin{equation} H(\mathbf{X, Y}) = H(\mathbf{X}) + H(\mathbf{Y}) - I(\mathbf{X}; \mathbf{Y}) \end{equation}\]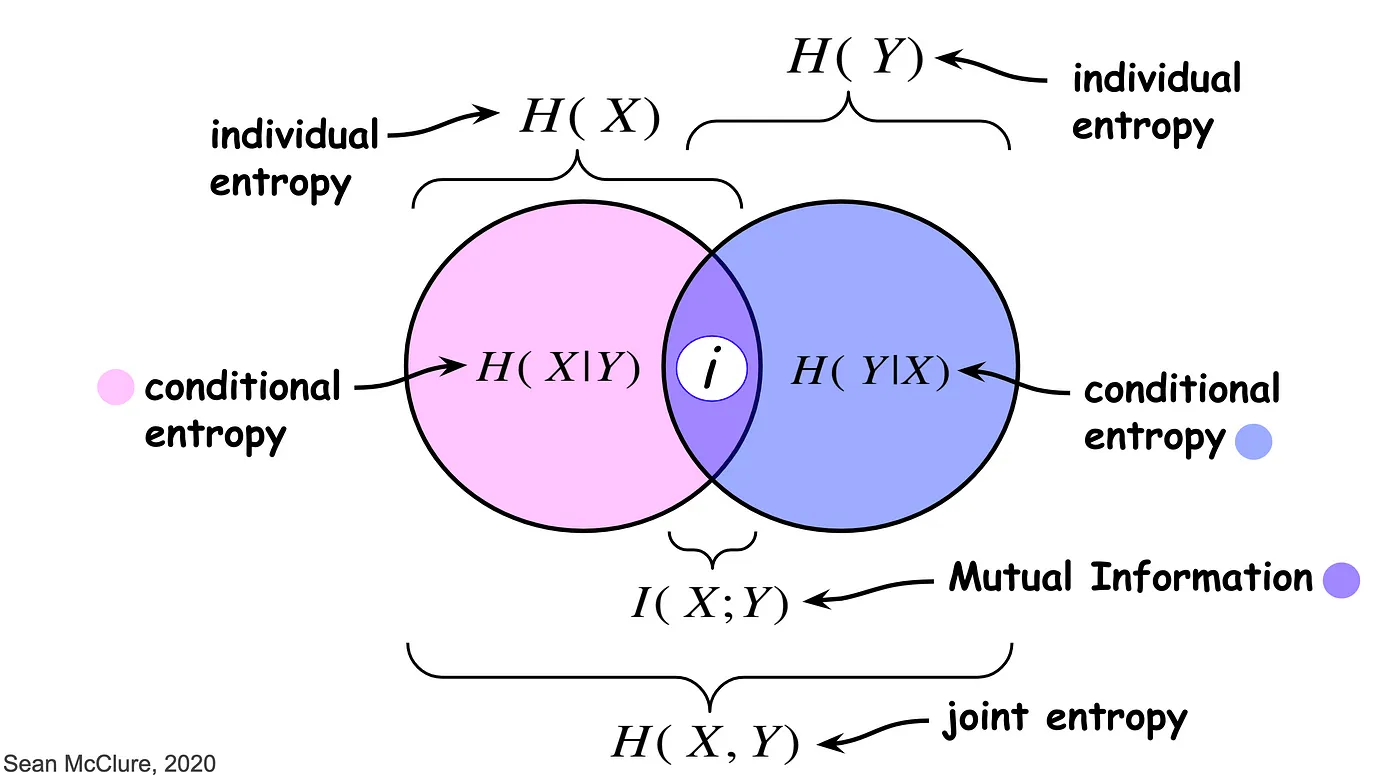
Cross Entropy
그러면 cross entropy는 무엇일까? Mutual information이 서로 다른 랜덤 변수, 즉 다른 사건에 대해 다루었다면, cross entropy는 같은 랜덤 변수에 초점을 둔다. Cross entropy는 같은 사건(같은 random variable $X$)을 공유하는 두 확률분포 $P$와 $Q$에 대해서, $P$를 $Q$로 표현할 떄 얼마나 잘 표현될 수 있는가를 나타낸다. 이를 단순하게 표현하면 실제 분포 $P$에 대한 $Q$의 예측에 대한 정보량의 기대값이라고 요약할 수 있다.
왜 정보량의 기대값인가? 실제 확률분포(true distribution) $P$에 대해 데이터로 표현된(모델링을 통해 구한, estimated probability distribution) 확률 분포 $Q$로 데이터를 전송(그래서 cross이다)한다고 하자. 이 전송 이벤트의 정보량(i.e. 비트수)이 평균적으로 얼만큼 되는지 계산하는 것이 Cross Entropy이다.
수학적으로는 다음과 같이 $P$에 대한 Expected Value형태로 $Q$를 계산하게된다.
\[\begin{align} H(P, Q) &= - \mathbb{E}_{x \sim P(X)} \log{Q(X)} \\ &= - \sum_{x\in X} P(x) \log{Q(x)} \end{align}\]예측이 정확해질수록, 불확실성이 낮아지게 되고, 두 확률분포 사이의 엔트로피는 0에 가까워진다.
Kullback–Leibler Divergence
Cross Entropy의 정의는 true distribution $P$를 표현하기 위한 estimated probability distribution $Q$의 정보량이었다. 이는 $P$의 자체적인 엔트로피와 $P$로부터 $Q$의 상대적인 엔트로피 값의 합으로 표현할 수 있을 것이다.
이 때 이 $P$로부터 $Q$의 상대적인 엔트로피(relative entropy)를 Kullback–Leibler Divergence 혹은 KL Divergence라고 한다. 모델링 관점에서는 이는 $Q$를 $P$에 대해 모델링할 때, 잃어버리는 정보량을 정량화한 것이라고 볼 수 있다.
수학적 기호로는 \(D_{KL}(P \;\|\; Q)\)라고 표현하며 정의는 다음과 같다.
\[\begin{equation} D_{KL}(P \;\|\; Q) := \sum_{x \in \mathcal{X}} P(X) \log{\left( \dfrac{P(x)}{Q(x)} \right)} \end{equation}\]KL Divergence는 다음과 같은 중요한 특징 2가지가 있다.
-
KL Divergence is non-negative 수학적으로 증명할 수도 있지만 너무 길어지길래 링크로 대체한다. 증명 ( \(D_{KL}(P \;\|\; Q) \geq 0\) )
-
KL Divergence is asymmetric 서로 다른 랜덤변수에 대해서는 대칭적인 Mutual Information과는 달리 같은 랜덤변수를 모델링할때는, A를 B로 모델링할때와 B를 A로 모델링할떄 잃어버리는 정보량이 다를 수 있기에 KL Divergence는 비대칭적인 값이라고 할 수 있다. 수학적으로는 다음과 같이 표현한다.
\[\begin{equation} D_{KL}(P \;\|\; Q) \neq D_{KL}(Q \;\|\; P) \end{equation}\]증명은 해당 링크에서 확인할 수 있다.
KL Divergence and Cross Entropy
$P$를 $Q$로 모델링할 때 동일하지 않은 분포라면 추가적인 정보가 필요하다. 전송 event(Cross Entropy)는 원래 가지고 있던 distribution의 entropy($H(P)$)와 $P$에서 $Q$로 전송할때 상대적인 엔트로피의 합이라고 할 수 있다.
이를 수식으로는 다음과 같이 표현한다. 이 떄, $H(P, Q)$는 $P$와 $Q$의 Cross entropy, $H(P)$는 $P$의 엔트로피 혹은 $P$에서 $P$의 cross entropy이다.
\[\begin{equation} H(P, Q) = H(P) + D_{KL}(P \;\|\; Q) \end{equation}\]역으로
\[\begin{align} D_{KL}(P \;\|\; Q) &= H(P, Q) - H(P) \\ &= \sum_{x \in \mathcal{X}} P(x) \log{\dfrac{P(x)}{Q(x) }} \\ &= \sum_{x \in \mathcal{X}} P(x) \log{\dfrac{1}{Q(x) }} - \sum_{x \in \mathcal{X}} P(x) \log{\dfrac{1}{P(x) }} \\ &= \sum_{x \in \mathcal{X}} P(x) \log{P(x)} - \sum_{x \in \mathcal{X}} P(x) \log{Q(x)} \end{align}\]Loss function의 의미로는 KL Divergence를 쓰는게 맞다. 하지만 현실적으로 모델링의 관점에서 실제 분포 $P$를 정확히 알 수 없어 $H(P)$를 알 수 없기에, KL Divergence를 최소화 하는것을 cross entropy를 minimize하는 것으로 바꾸어서 풀게된다. 간접적인 최소화라고 할 수 있다. 따라서 보통 분류문제의 loss를 cross entropy로 대신해서 사용한다.
스팸메일 분류를 예로 들어보자. 실제 스팸일 확률은 80%, 하지만 모델은 70%로 예측한다고 해보자. 이를 표로 표현하면 다음과 같다.
| 스팸 O | 스팸 X | |
|---|---|---|
| P(실제) | 0.8 | 0.2 |
| Q(모델) | 0.7 | 0.3 |
-
Cross Entropy ($H(P, Q)$): 각 $P$의 이벤트에 대해 $Q$를 사용하여 계산된 기대정보량은 다음과 같다.
\[\begin{align*} H(P, Q) &= - \sum_{x\in X} P(x) \log{Q(x)} \\ &= -(0.8 \log{0.7} + 0.2 \log{0.3}) \end{align*}\] -
KL Divergence ($D_{KL}(P \;|\; Q)$): 이는 $P$와 $Q$ 간의 상대적 엔트로피, 즉 $Q$가 $P$를 얼마나 잘 나타내는지의 척도이다.
\[\begin{align*} D_{KL}(P \;\|\; Q) &= \sum_{x \in \mathcal{X}} P(x) \log{P(x)} - \sum_{x \in \mathcal{X}} P(x) \log{Q(x)} \\ &= 0.8 \log{\dfrac{0.8}{0.7}} + 0.2 \log{\dfrac{0.2}{0.3}} \end{align*}\] -
$P$의 엔트로피 ($H(P)$): 단순히 실제 분포 $P$의 엔트로피이다. \(\begin{equation*} H(P) = - (0.8 \log{0.8} + 0.2 \log{0.2}) \end{equation*}\)
Final Thoughts
지금까지 Cross Entropy Loss를 이해하기 위해 odds부터 시작하여 기본적인 내용을 다뤄보았다. Cross Entropy는 단순 분류모델뿐만 아니라 LLM(Large Language Model)에서도 중요하게 쓰이는 개념이다. LLM의 기본적인 개념은 모델이 알고있는 단어들 중에서 가장 높은 확률의 다음 단어를 예측하는 모델이기 때문이다.
Reference
- Shannon, Claude Elwood. 1948. “A Mathematical Theory of Communication.” The Bell System Technical Journal 27 (3): 379–423.
- MacKay, David JC. 2003. Information Theory, Inference and Learning Algorithms. Cambridge university press.