From EBM to NCSN

Introduction

이전 포스트에 이어서 [1]를 바탕으로 NCSN(Noise Conditional Score Network)을 깊게 파보는 포스트를 작성하려고 한다.

Deep Learning Model은 보통 확률을 출력하기를 원한다. 하지만, 딥러닝에서 확률의 대전제인 ‘모든 확률의 합은 1’을 만족시키기 위해서는 차원의 저주때문에 계산적으로 많은 비용이 든다.

기존 모델들은 이 계산을 피하기 위해 모델 구조를 억지로 단순화하거나(Normalizing Flow), 아예 확률 계산을 포기하는(GAN) 타협을 했다. 하지만 이를 타협하지 않고, 확률을 Energy와 결합하여 ‘데이터와 비슷하면 낮은 에너지, 비슷하지 않으면 높은 에너지라고 정의하자. 합이 1이 되는 건 나중에 생각하고, 가장 표현력이 좋은 네트워크를 쓰자’라는 접근을 취한 Energy Based Model (EBMs)가 있다.

Energy Based Model (EBMs)은 분포 $p(\mathbf{x})$를 데이터 밀도가 높은 영역에서는 낮은 에너지를 갖는 Energy Landscape으로 표현한다. EBM에서의 샘플링은 일반적으로 Langevin Dynamics를 통해 이루어지며, 샘플을 고밀도 영역으로 이동시키기 위해 Energy Landscape의 기울기, 즉 Score Function $\nabla_{\mathbf{x}} \log p(\mathbf{x})$를 정의하고 추적한다.

여기서의 핵심은 Energy 혹은 확률 분포를 정확히 아는 것이 아닌 그 변화량만 추적한다는 것이다. 이를 통해 Score Function을 알면 계산 불가능한 정규화 상수 $Z$ 없이도 샘플 생성이 가능하다. Score는 샘플을 확률이 더 높은 방향으로 안내하는 벡터 필드 역할을 한다.

Score-based Diffusion Models은 깨끗한 데이터 분포 대신, 가우시안 노이즈가 점진적으로 추가된 분포들의 시퀀스를 고려한다. 이렇게 노이즈가 가해진 분포의 Score는 학습하기가 상대적으로 용이하며, 모델은 이 시퀀스에 대한 Score Function들을 근사적으로 학습한다.

학습된 Score Function들은 잡음이 낀 샘플을 단계적인 잡음 제거(progressive denoising)를 통해 데이터 분포로 되돌리는 강력한 벡터 필드를 형성한다. Noise Conditional Score Networks (NCSN)는 이러한 Score-based 모델의 대표적인 구현체이다.

Energy Based Models

$\mathbf{x} \in \mathbb{R}^\mathcal{D}$을 data point라고 하자. EBM은 확률 밀도를 에너지 함수 $E_\phi (\mathbf{x})$로 정의한다. $E_\phi (\mathbf{x})$는 낮은 에너지가 높은 확률밀도가 되도록 $\phi$를 통해 파라미터화한다. 이는 다음과 같이 수식으로 표현할 수 있다.

\[\begin{align} p_\phi (\mathbf{x}) := \dfrac{\exp{(-E_\phi (\mathbf{x}))}}{Z_\phi}, \quad Z_\phi := \int_{\mathbb{R}^\mathcal{D}} \exp{(-E_\phi (\mathbf{x}))} d \mathbf{x} \end{align}\]

이 때 $Z_\phi$는 Partition function이라 불리우며 확률에서의 normalization을 보장하는 함수이다.

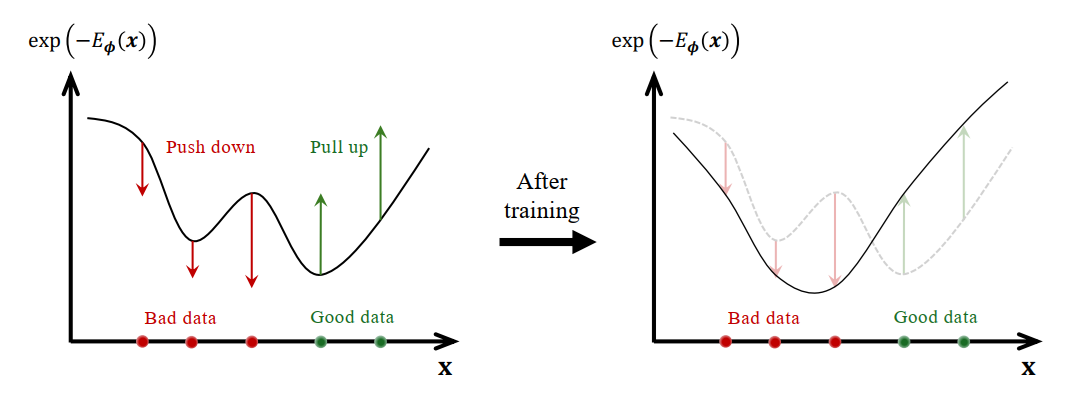
\[\int_{\mathbb{R}^\mathcal{D}} p_\phi (\mathbf{x}) d \mathbf{x} = 1\]

Illustration of EBM training

EBM은 학습을 통해 나쁜 데이터(빨간색)에서 확률 밀도를 낮추고 (에너지 상승), 반대로 좋은 데이터는(파란색) 확률 밀도를 높이는(에너지 하강) 방식으로 훈련 한다.

Partition function $Z_\phi$는 전체 확률의 합을 1로 맞추기 때문에 에너지 값 자체의 값은 중요하지 않고, 에너지의 상대적인 값만이 중요하다. 이 과정에서 한쪽의 에너지를 낮추기 위해선 (확률을 높이면), 다른쪽의 에너지를 높여야하는 과정(확률을 낮추는 과정)이 필수이다. 풍선같이 한쪽을 누르면 다른쪽이 부푸는 작업이라고 할 수 있고, EBM은 이런 trade-off를 만족하면서 전체의 균형 (에너지는 항상 일정)을 맞춰야하는 작업이다.

Challenges of Maximum Likelihood Training in EBMs

MLE(Maximum Likelihood Estimation)을 통해 EBM을 훈련하는 것은 다음과 같은 loss function을 통해 표현할 수 있다.

\[\begin{align} \mathcal{L}_{MLE}(\phi) &= \mathbb{E}_{p_{\textrm{data}} (\mathbf{x})} \left[ \log \dfrac{\exp{(-E_\phi (\mathbf{x}))}}{Z_\phi} \right] \\ &= - \underbrace{\mathbb{E}_{p_{\textrm{data}}} [E_\phi (\mathbf{x})]}_{\textrm{lowers energy of data}} - \underbrace{\log \int \exp{(-E_\phi (\mathbf{x}))} d \mathbf{x}}_{\textrm{global regularization}} \end{align}\]

이 때 $Z_\phi = \int \exp{(-E_\phi (\mathbf{x}))} d\mathbf{x}$이다. 첫번쨰 term은 실제 데이터의 에너지를 낮추고, 두번째 term은 $Z_\phi$를 통해 전체 normalization을 컨트롤하는 역할이다. 하지만, 고차원에서 $\log{Z_\phi}$와 그것의 gradient를 계산하는 것은 계산 비용이 무한대에 가까워서 거의 불가능하다고 볼 수 있다. 이를 해결하고자 하는 방법 중 하나가 score matching이다.

즉 결론은 EBM을 훈련하기 위해서는 Partition function $Z_\phi = \int \exp{(-E_\phi (\mathbf{x}))} d\mathbf{x}$ 계산이 필요하고, 이는 intractable하기 때문에 score matching을 사용한다.

Score Matching

Motivation: What Is the Score?

단순히 말해서 Score는 Gradient이다. $\mathbb{R}^\mathcal{D}$의 $p(\mathbf{x})$가 있을 때, score function은 log-density의 gradient로 정의된다.

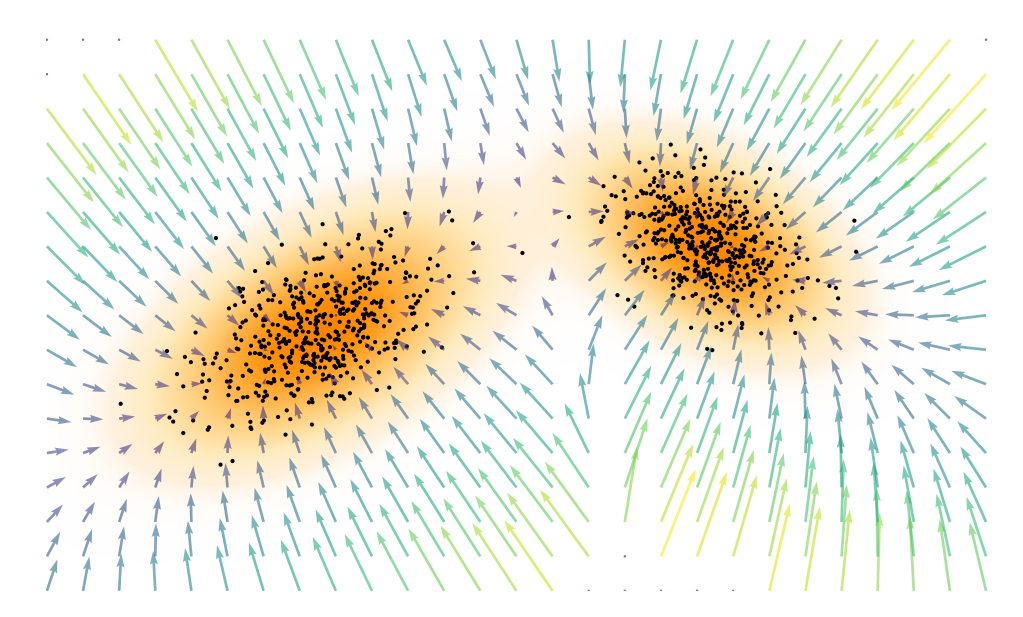
\[\begin{align} \mathbf{s}(\mathbf{x}) := \nabla_\mathbf{x} \log p(\mathbf{x}), \quad \mathbf{s}: \mathbb{R}^\mathcal{D} \rightarrow \mathbb{R}^\mathcal{D} \end{align}\]

Score function 아래 그림처럼 높은 확률 쪽으로 향하는 벡터 필드(벡터장)인 것이다. 1차원 적으로는 Figure 1의 기울기라고 보면 된다.

Illustration of score vector fields

이를 통해 다음과 같은 이점이 있다.

Normalization constant $Z_phi$로 부터의 자유

기존의 $p_\phi (\mathbf{x}) := \dfrac{\exp{(-E_\phi (\mathbf{x}))}}{Z_\phi}$의 정의처럼 Unnormalized density $\bar{p} (\mathbf{x})$가 있다하면 다음과 같이 간략하게 쓸 수 있다.

\[\begin{equation*} p(\mathbf{x}) = \dfrac{\bar{p}(\mathbf{x})}{Z}, \quad Z = \int \bar{p} (\mathbf{x}) d \mathbf{x} \end{equation*}\]

Gradient를 구하기 위해 미분을 하면 $Z$는 $\mathbf{x}$에 대해서는 상수이기 때문에 (모든 $\mathbf{x}$에 대해 적분하는 값이므로) $\nabla_\mathbf{x} Z=0$이 된다.

\[\begin{equation*} \nabla_\mathbf{x} \log p(\mathbf{x}) = \nabla_\mathbf{x} \log \bar{p}(\mathbf{x}) -\underbrace{\nabla_{\mathbf{x}} \log Z}_{=0} = \nabla_\mathbf{x} \bar{p}(\mathbf{x}) \end{equation*}\]

즉 gradient 입장에서는 $\nabla_\mathbf{x} \log p(\mathbf{x}) = \nabla_\mathbf{x} \bar{p}(\mathbf{x})$인 것이다.

A Complete Representation

확률 밀도 함수 $p(\mathbf{x})$ 대신 $\mathbf{s}(\mathbf{x})$를 쓰면 표현력이 떨어지거나 정보의 손실이 일어나지 않을까라는 생각을 할 수 있다.

\[\begin{equation*} \log p(\mathbf{x}) = \log p(\mathbf{x}_0) + \int_0^1 \mathbf{s} (\mathbf{x}_0 + t(\mathbf{x} - \mathbf{x}_0))^{\mathsf{T}} (\mathbf{x} - \mathbf{x}_0) dt \end{equation*}\]

위 식은 \(\mathbf{x}(t) = \mathbf{x}_0 + t(\mathbf{x} - \mathbf{x}_0)\), \(\mathbf{s}(x) := \nabla_\mathbf{x} \log p(\mathbf{x})\), 그리고 다음과 같은 Chain rule을 사용하여 구할 수 있다.

\[\begin{align*} \dfrac{d}{dt} \log p(\mathbf{x}(t)) &= \nabla_\mathbf{x} \log p(\mathbf{x}(t)) \cdot \dfrac{d \mathbf{x}(t)}{dt} \\ &= \mathbf{s}(\mathbf{x}) \cdot (\mathbf{x} - \mathbf{x}_0) \\ &= \mathbf{s}(\mathbf{x})^{\mathsf{T}}(\mathbf{x} - \mathbf{x}_0) \\ &= \mathbf{s}(\mathbf{x}_0 + t(\mathbf{x} - \mathbf{x}_0))^{\mathsf{T}}(\mathbf{x} - \mathbf{x}_0) \end{align*}\]

여기서 $\dfrac{d}{dt} \log p(\mathbf{x}(t))$를 적분식으로 풀면 위 식이 나오게 된다. 이 떄 $\mathbf{x}_0$은 reference point이고, $\log p (\mathbf{x}_0)$는 $\int \log p (\mathbf{x}) = 1$로 만드는 normalization을 위해 고정이 되므로 $\mathbf{s}$로부터 $p(\mathbf{x})$를 구할 수 있다.

Training EBMs via Score Matching

다시 한번 정리해보면 모델의 확률 밀도 $p_\phi (\mathbf{x})$ 대신에 모델의 score $\nabla_\mathbf{x} \log p_\phi (\mathbf{x}) = -\nabla_\mathbf{x} E_\phi (\mathbf{x})$를 타겟으로 한다. EBM은 Score matching을 통해 확률 밀도 $p$대신에 model score (모델의 score) $\nabla_\mathbf{x} p_\phi (\mathbf{x})$와 data score (unknown) $\nabla_\mathbf{x} p_{\textrm{data}} (\mathbf{x})$의 차이를 최소화 하는 방향으로 훈련을 진행한다.

그리고 $\nabla_\mathbf{x} p_{\textrm{data}} (\mathbf{x})$는 unknown이라 구할 수 없으므로 부분적분을 통해 $p_{\textrm{data}} (\mathbf{x})$를 소거하고, 이를 기대값($\mathbb{E}$) 형태의 연산으로 바꾼다. 진짜 데이터가 있는데 왜 unknown이냐하면, data가 있는 부분에서는 확률이 1이고 나머지는 0인 dirac delta로 표현되는 확률 분포가 나오는데 이는 기울기를 구하기 어렵다. 이 과정을 다음과 같이 표현한다.

\[\begin{align} \mathcal{L}_{SM} (\phi) &=\dfrac{1}{2} \mathbb{E}_{p_{\textrm{data}}(\mathbf{x})} \|\nabla_\mathbf{x} p_\phi (\mathbf{x}) - \nabla_\mathbf{x} p_{\textrm{data}} (\mathbf{x})\|^2_2 \\ &=\mathbb{E}_{p_{\textrm{data}}(\mathbf{x})} \left[ Tr(\nabla_\mathbf{x}^2 E_\phi (\mathbf{x})) + \dfrac{1}{2} \|\nabla_\mathbf{x} E_\phi (\mathbf{x}) \|^2_2 \right] + C \end{align}\]

이 때 $\nabla_\mathbf{x}^2 E_\phi (\mathbf{x})$는 $E_\phi$의 Hessian이고 $C$는 constant이다.

이 전체적인 과정은 뒤에서 자세하게 증명하겠지만, 일단 지금까지 흐름을 정리하면 이렇다.

1. $p_\phi (\mathbf{x})$에 집중하는 EBM대신 gradient인 score function에 대해 정리한다.
   1. $p_\phi (\mathbf{x})$를 사용하는 경우 partition function $Z$가 필요하다.
   2. 그러나 고차원에서 $Z$를 구하는 것은 매우 계산적으로 비효율 적이고, 모델에서 샘플링해서 MCMC를 써도 오래 걸린다. 즉 intractable하다.
2. Score Matching을 통해 모델과 데이터의 Score의 차이를 감소하는 방향으로 EBM을 훈련한다.
3. Data Score는 unknown이므로 Score Matching함수를 실제 데이터에 대한 함수 (\(\mathbb{E}_{p_{\textrm{data}}(\mathbf{x})}\))로 변환한다.
   1. 데이터가 존재하지 않는 구역과 존재하는 구역 사이의 gradient는 구하기 어렵다.
4. 이를 통해 다음과 같은 효과를 얻는다.
   1. Partition function $Z$제거
   2. MCMC와 같은 모델 샘플링을 회피
   3. 단점은 $\nabla_\mathbf{x}^2 E_\phi (\mathbf{x})$가 2차 미분이라 계산량이 높다는 것

Langevin Sampling with Score Functions (Inference)

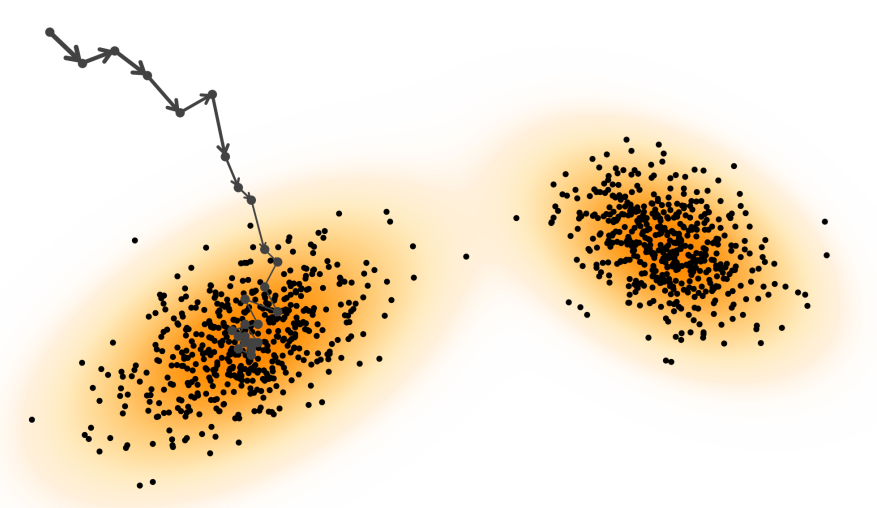
앞서 설명했듯, 훈련과정을 통해 score function \(\mathbf{s}_\phi (\mathbf{x}) = \nabla_\mathbf{x} \log p_\phi (\mathbf{x}) \approx -\nabla_\mathbf{x} E_\phi (\mathbf{x})\)를 구한다. 실제 추론 단계에서는 Langevin Dynamics을 사용한다. 이는 무작위 초기 지점(Random noise)으로부터 학습된 Score를 따라 데이터 밀도 가 높은 영역(High Density Region)으로 점진적으로 이동하는 과정이다. 이는 단순히 기울기만으로 최적화하지 않고, 노이즈를 주입하여 샘플링하는 것이 핵심이다. 노이즈가 없다면 가장 가까운 Local Minima에 갇혀 항상 똑같거나 획일화된 이미지가 생성될 위험이 있다. 즉, 노이즈는 생성 결과의 다양성을 확보하는 안전장치 역할을 한다.

Illustration of Langevin sampling

Discrete-Time Langevin Dynamics

원래 Langevin Dynamics는 브라운 운동을 설명하기 위해 나온 개념이다. 에너지가 낮은 상태로 가려는 확정적인 힘 Drift와 분자 운동으로 인한 무작위적인 힘인 Diffusion에 움직이는 분자운동을 묘사한다.

현재까지 본 EBM입장에서는 Score가 Drift가 되고 여기에 Noise(일반적으론 Guassian Noise)가 들어가면서 Diffusion 역할을 한다.

이를 Discrete-time관점에서 작성하면 다음과 같다. 실제로도 스텝별로 노이즈를 추가하면서 Langevin Dynamics를 적용하기 때문에 아래 식이 더 익숙할 것이다.

\[\begin{align} \mathbf{x}_{n+1} = \mathbf{x}_n - \eta \nabla_\mathbf{x} E_\phi (\mathbf{x}) + \sqrt{2\eta} \mathbf{\epsilon}_n, \quad n=0,1,2,\dots, \end{align}\]

이 때 $\mathbf{x}_0$은 Gaussian 분포와 같이 특정 분포에서 초기화 되고 $\eta >0$은 step size, 그리고 $\mathbf{\epsilon}_n \sim \mathcal{N}(\mathbf{0}, \mathbf{I})$은 Gaussian noise이다.

이 때 Score function의 정의 \(\nabla_\mathbf{x} \log p_\phi (\mathbf{x}) \approx -\nabla_\mathbf{x} E_\phi (\mathbf{x})\)를 결합하면 다음 식으로 변환된다.

\[\begin{align} \mathbf{x}_{n+1} = \mathbf{x}_n + \eta \nabla_\mathbf{x} \log p_\phi (\mathbf{x}) + \sqrt{2\eta} \mathbf{\epsilon}_n, \quad n=0,1,2,dots, \end{align}\]

Continuous-Time Langevin Dynamics

만약 $\eta \rightarrow 0$가 된다면 즉 step size가 매우 작아진다면 위 식은 Continuous process로 생각할 수 있고, 이를 Langevin Stochastic Diffusion Equations (SDE)라고 한다.

\[\begin{align} d\mathbf{x} = \nabla_\mathbf{x} \log p_\phi (\mathbf{x} (t)) dt + \sqrt{2} d \mathbf{w} (t) \end{align}\]

이 때 $\mathbf{w}(t)$는 Wiener process라고 하며 Standard Brownian motion을 나타낸다. 보통은 Continuous-Time Langevin Dynamics인 SDE를 먼저 배우고 위 식을 Euler-Maruyama discretization을 통해 Discrete-Time Langevin Dynamics으로 넘어간다. 하지만, NCSN입장에선 처음에는 step을 명시적으로 지정하는 Discrete 버전을 것을 먼저 찾았고, [2]을 통해 Continous한 SDE로 일반화하였기 때문에 반대로 소개한다.

Why Langevin Sampling?

Langevin Sampling의 기원을 물리적인 관점, 특히 유체 속 입자의 브라운 운동(Brownian Motion)에서 찾아보자.

고전적인 뉴턴역학(Newtonian dynamics)에서는 물체의 움직임은 $F=ma$에 따라 힘과 가속도의 관계로 설명된다. 하지만 꿀물처럼 점성이 매우 높은 유체 속에 있는 가벼운 입자를 생각해보면, 이 경우 관성(Inertia)의 영향은 무시할 수 있고, 입자의 속도는 가해지는 힘에 비례하게 된다(Overdamped Langevin Dynamics).

따라서 어떤 포텐셜 에너지 장(Force field) 안에서 입자의 움직임은 다음과 같은 1차 미분방정식(ODE)으로 단순화하여 표현할 수 있다.

\[\begin{equation} d \mathbf{x} (t) = - \nabla_\mathbf{x} E_\phi (\mathbf{x}(t)) dt \end{equation}\]

이 식은 deterministic하게 Energy가 낮은 쪽으로 particle을 이동시키는 역할을 한다. 그러나 앞서 언급한 것처럼 이런 경우 local minima에 빠질 확률이 높다. 이를 회피하기 위해 Langevin dynamics는 다음과 같은 SDE를 통해 stochastic perturbation을 주입한다. 이 때 $d \mathbf{w}(t)$는 Standard Brownian motion이다.

\[\begin{equation} d \mathbf{x} (t) = - \nabla_\mathbf{x} E_\phi (\mathbf{x}(t)) dt + \underbrace{\sqrt{2} d \mathbf{w}(t)}_{\textrm{injected noise}} \end{equation}\]

노이즈 항은 Local minima를 벗어나게 해주며 시간이 충분히 흐르면 입자의 궤적(trajectory)이 에너지 함수에 대응하는 볼츠만 분포(Boltzmann distribution)를 따르게 만든다.

\[\begin{equation} p_\phi (\mathbf{x}) \propto e^{-E_\phi (\mathbf{x})} \end{equation}\]

결국 EBM은 샘플들을 높은 밀도의 확률로 이동시키는 Score라는 Force field를 학습하게 된다. Langevin sampling을 iteratively하게 적용하면 우리가 원래 목표로 했던 target distribution인 data의 distribution을 얻게 되는 것이다.

참고로 예전에도 난류의 External forcing에서 Langevin dyanmics에 관한 글을 작성한 적이 있다.

Inherent Challenges of Langevin Sampling

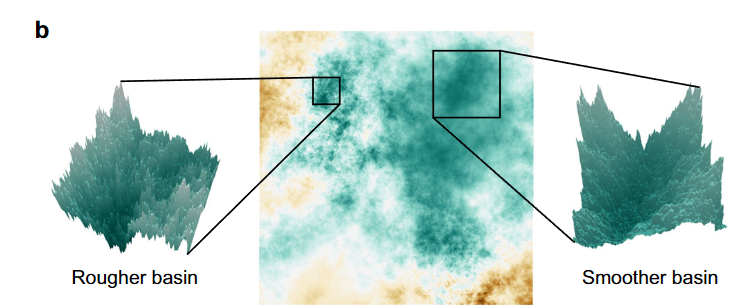
그러나 실제 데이터 분포는 복잡하고 고차원으로 이루어져있다. 이를 멀리 떨어져 있는 수많은 계곡이 있는 거친 지형(Rugged Landscape)처럼 생각할 수 있다.

Rugged Loss Landscape

하지만 Langevin dynamics는 현재 위치에서 조금씩만 이동하는 국소적인 업데이트(Local update) 방식이다. 때문에 하나의 계곡(Mode)에 들어가면, 데이터가 없는 허허벌판(Low density region)을 건너 다른 계곡으로 이동하는 데 너무 많은 시간이 걸리게 된다.

게다가, 고차원으로 갈수록 데이터 간의 거리는 멀어지고 대부분 빈 공간으로 가득차게 된다. 예를 들어 2차원 hypercube(정사각형)안에서의 2차원 hypersphere(원)의 비율은 $\pi/4=78.5\%$이지만, 10차원만 되어도 $\pi^5/120\cdot 2^10 = 0.25\%$ 즉 99.75%가 빈공간이다.

또한 하이퍼 파라미터인 스텝 사이즈, 노이즈 크기, 반복 횟수 등에 너무 민감해지므로 이를 해결하기 위해 NCSN(Noise Conditional Score Network)가 등장하게 된다.

From Energy-Based to Score-Based Generative Models

Illustration of Score Matching

지금까지 살펴봤듯 데이터 확률 분포 자체를 직접 학습하는 것이 아니라, 그것의 Gradient인 Score만 학습해도 충분하다는 것을 확인했다.

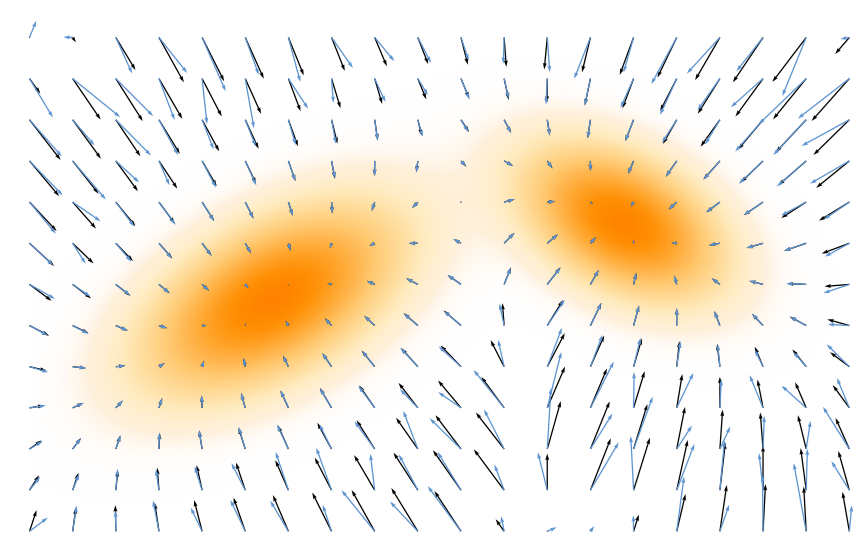
이를 모델링 관점에서 보면 신경망이 예측한 Score인 $\mathbf{s}_\phi (\mathbf{x})$와 실제 데이터의 ground truth score $\mathbf{s}(\mathbf{x})$의 차이를 MSE Loss를 이용하여 최소화하는 과정을 통해 학습한다. 물론 앞서 언급했듯 실제 Score는 알 수 없기 때문에 Score Matching기법을 통해 간접적으로 학습한다.

시각적으로 보면 위 그림에서 ‘신경망이 만든 벡터장’을 ‘실제 데이터가 만드는 벡터장’과 똑같은 모양이 되도록 끼워 맞추는 과정이라고 이해할 수 있다.

현재 섹션에서는 이 과정을 좀 더 수식 증명과 함께 분석하고자 한다.

Training with Score Matching

Score Matching

앞서 언급했던 것처럼 모델의 score와 실제 score를 근사시키는 방향으로 모델을 훈련한다.

\[\begin{align} \mathbf{s}_\phi (\mathbf{x}) \approx \mathbf{s} (\mathbf{x}) \end{align}\]

이는 다음과 같은 MSE Loss를 사용함을 뜻한다.

\[\begin{equation} \mathcal{L}_{SM} (\phi) =\dfrac{1}{2} \mathbb{E}_{\mathbf{x} \sim p_{\textrm{data}}(\mathbf{x})} \left[ \| \mathbf{s}_\phi (\mathbf{x}) - \mathbf{s} (\mathbf{x}) \|^2_2 \right] \end{equation}\]

Tractable Score Matching

하지만 앞서 언급한 것 중 하나가 \(\mathbf{s}_\phi (\mathbf{x})\) 를 구하는 것은 intractable하다는 것이다.

그러나 [3]에서는 부분적분을 통해 \(\mathcal{L}_{SM} (\phi)\)를 \(mathbf{s}_\phi (\mathbf{x})\)와 data sample만으로 외존하는 형태(\(\tilde{\mathcal{L}}_{SM} (\phi)\))로 변환했다.

\[\begin{equation} \mathcal{L}_{SM} (\phi) = \tilde{\mathcal{L}}_{SM} (\phi) + C \end{equation}\]

이 때 \(\tilde{\mathcal{L}}_{SM} (\phi)\)은 다음과 같이 표현한다.

\[\begin{equation} \tilde{\mathcal{L}}_{SM} (\phi) := \mathbb{E}_{\mathbf{x} \sim p_{\textrm{data}}(\mathbf{x})} \left[ Tr(\nabla_\mathbf{x}\mathbf{s}_\phi (\mathbf{x})) + \dfrac{1}{2} \| \mathbf{s}_\phi (\mathbf{x}) \|^2_2 \right] \end{equation}\]

이 때 $C$는 상수이며 $\phi$에 의존하지 않는다. 또한 이렇게 구한 minimizer 는 \(\mathbf{s}^* (\cdot) = \nabla_\mathbf{x} \log p (\cdot)\)이다.

이는 다음과 같이 증명할 수 있다.

우선 \(\mathcal{L}_{\text{SM}}(\phi)\)의 Squared difference를 전개한다.

\[\begin{align} \mathcal{L}_{\text{SM}}(\phi) &= \frac{1}{2} \mathbb{E}_{\mathbf{x} \sim p_{\text{data}}(\mathbf{x})} \left[ \|\mathbf{s}_{\phi}(\mathbf{x})\|_2^2 - 2 \langle \mathbf{s}_{\phi}(\mathbf{x}), \mathbf{s}(\mathbf{x}) \rangle + \|\mathbf{s}(\mathbf{x})\|_2^2 \right] \\ &= \frac{1}{2} \mathbb{E}_{\mathbf{x} \sim p_{\text{data}}(\mathbf{x})} \left[ \|\mathbf{s}_{\phi}(\mathbf{x})\|_2^2 \right] - \mathbb{E}_{\mathbf{x} \sim p_{\text{data}}(\mathbf{x})} \left[ \langle \mathbf{s}_{\phi}(\mathbf{x}), \mathbf{s}(\mathbf{x}) \rangle \right] \\ &\quad + \frac{1}{2} \mathbb{E}_{\mathbf{x} \sim p_{\text{data}}(\mathbf{x})} \left[ \|\mathbf{s}(\mathbf{x})\|_2^2 \right] \end{align}\]

여기서 문제되는 term은 \(\mathbb{E}_{\mathbf{x} \sim p_{\text{data}}(\mathbf{x})} \left[ \langle \mathbf{s}_{\phi}(\mathbf{x}), \mathbf{s}(\mathbf{x}) \rangle \right]\)이다. pdf에서는 cross-product term이라고 했지만 이건 이차식을 전개할때의 cross-product이지 벡터의 외적을 뜻하는 cross-product가 아니다.

\(p_{\text{data}}(\mathbf{x})\)가 $0$이 아니라면 \(\nabla_\mathbf{x} \log p_{\text{data}}(\mathbf{x}) = \dfrac{\nabla_\mathbf{x} p_{\text{data}}(\mathbf{x})}{p_{\text{data}}(\mathbf{x})}\) (로그 미분식) 을 사용할 수 있다.

\[\begin{align*} \mathbb{E}_{\mathbf{x} \sim p_{\text{data}}(\mathbf{x})} \left[ \langle \mathbf{s}_{\phi}(\mathbf{x}), \mathbf{s}(\mathbf{x}) \rangle \right] &= \int \left( \mathbf{s}_\phi (\mathbf{x})^\mathsf{T} \mathbf{s} (\mathbf{x}) \right) p_{\text{data}}(\mathbf{x}) d \mathbf{x} \\ &= \int \left( \mathbf{s}_\phi (\mathbf{x})^\mathsf{T} \nabla \log p_{\text{data}}(\mathbf{x}) \right) p_{\text{data}}(\mathbf{x}) d \mathbf{x} \\ &= \int \left( \mathbf{s}_\phi (\mathbf{x})^\mathsf{T} \dfrac{\nabla_\mathbf{x} p_{\text{data}}(\mathbf{x})}{p_{\text{data}}(\mathbf{x})} \right) p_{\text{data}}(\mathbf{x}) d \mathbf{x} \\ &= \int \mathbf{s}_\phi (\mathbf{x})^\mathsf{T} \nabla_\mathbf{x} p_{\text{data}}(\mathbf{x}) d \mathbf{x} \\ &= \sum_{i=1}^D \int \mathbf{s}^{(i)}_\phi (\mathbf{x}) \partial x_i p_{\text{data}}(\mathbf{x}) d \mathbf{x} \end{align*}\]

이 때 $ \mathbf{s}^{(i)}_\phi (\mathbf{x})$는 score function의 i-th component이고, 앞으로 진행할 부분 적분을 손쉽게 하기 위해 내적을 성분별 곱의 합으로 표현한다.

\[\begin{equation*} \mathbf{s}_\phi (\mathbf{x})= \left( \mathbf{s}^{(1)}_\phi (\mathbf{x}), \mathbf{s}^{(2)}_\phi (\mathbf{x}), \dots, \mathbf{s}^{(D)}_\phi (\mathbf{x}) \right) \end{equation*}\]

이제 부분 적분을 적용하면 되는데, 데이터와 같은 경우는 경계를 가정하기 힘들기 때문에 일단 어떤 ball 안에 있다고 가정한다.

만약 $u,v$가 반지름 $R > 0$를 가지는 ball \(\mathbb{B}(\mathbf{0}, R) \subset \mathbf{R}^D\) 위의 실수 함수라고 가정하면, $i=1,2,\dots, D$에서 다음 부분 적분이 성립한다. 이 때, $\nu = (\nu_1, \dots, \nu_D)$는 boundary \(\partial \mathbb{B}(\mathbf{0}, R)\)로 향하는 outward unit normal function이며, $dS$는 \(\partial \mathbb{B}(\mathbf{0}, R)\)의 surface measure이다.

\[\begin{equation*} \int_{\mathbb{B}(\mathbf{0}, R)} u \partial_{x_i} v d \mathbf{x} = -\int_{\mathbb{B}(\mathbf{0}, R)} v \partial_{x_i} u d \mathbf{x} + \int_{\partial \mathbb{B}(\mathbf{0}, R)} u v \nu_i d S \end{equation*}\]

위 식에 \(u(\mathbf{x}) := \mathbf{s}^{(1)}_\phi (\mathbf{x})\), \(v(\mathbf{x}) := p_{\text{data}}(\mathbf{x})\)를 적용하고 다음을 가정한다. 왜냐하면 실제 데이터 분포 \(p_{\text{data}}(\mathbf{x})\)는 중심에서 멀어질수록 확률밀도는 지수적으로 감소하는 경우가 많기 때문이다. 그리고 신경망 \(\mathbf{s}^{(1)}_\phi (\mathbf{x})\) 은 아무리 커져도 대부분 polynomial형태로 증가한다. 따라서 \(p_{\text{data}}(\mathbf{x})\)가 압도하게 되고, 다음 가정이 성립한다. 그리고 이렇게 되면 부분적분의 두번쨰 항은 0이 된다.

\[\begin{equation*} | u(\mathbf{x}) u(\mathbf{x}) | \rightarrow 0 \quad \textrm{ as } R \rightarrow \infty \end{equation*}\]

모든걸 합치면

\[\begin{align*} \mathbb{E}_{\mathbf{x} \sim p_{\text{data}}(\mathbf{x})} \left[ \langle \mathbf{s}_{\phi}(\mathbf{x}), \mathbf{s}(\mathbf{x}) \rangle \right] &= \sum_{i=1}^D \int \mathbf{s}^{(i)}_\phi (\mathbf{x}) \partial x_i p_{\text{data}}(\mathbf{x}) d \mathbf{x} \\ &= - \sum_{i=1}^D \int \partial x_i \mathbf{s}^{(i)}_\phi (\mathbf{x}) p_{\text{data}}(\mathbf{x}) d \mathbf{x} \\ &= - \mathbb{E}_{\mathbf{x} \sim p_{\text{data}}(\mathbf{x})} \left[ Tr(\nabla_\mathbf{x} \mathbf{s}_\phi (\mathbf{x}))\right] \end{align*}\]

이 때 \(\partial x_i \mathbf{s}^{(i)}_\phi (\mathbf{x})\)가 Jacobian의 diagonal term이 되기 때문에 $\sum$을 통해 Trace만 남게 된다.

그러면 원래 \(\mathcal{L}_{\text{SM}}(\phi)\)와 결합하면

\[\begin{align*} \mathcal{L}_{\text{SM}}(\phi) &= \frac{1}{2} \mathbb{E}_{\mathbf{x} \sim p_{\text{data}}(\mathbf{x})} \left[ \|\mathbf{s}_{\phi}(\mathbf{x})\|_2^2 \right] - \mathbb{E}_{\mathbf{x} \sim p_{\text{data}}(\mathbf{x})} \left[ \langle \mathbf{s}_{\phi}(\mathbf{x}), \mathbf{s}(\mathbf{x}) \rangle \right] \\ &\quad + \frac{1}{2} \mathbb{E}_{\mathbf{x} \sim p_{\text{data}}(\mathbf{x})} \left[ \|\mathbf{s}(\mathbf{x})\|_2^2 \right] \\ &= \underbrace{\mathbb{E}_{\mathbf{x} \sim p_{\text{data}}(\mathbf{x})} \left[ Tr(\nabla_\mathbf{x} \mathbf{s}_\phi (\mathbf{x})) + \dfrac{1}{2} \|\mathbf{s}_{\phi}(\mathbf{x})\|_2^2 \right]}_{\tilde{\mathcal{L}}_{\text{SM}}(\phi)} \\ &\quad + \underbrace{\dfrac{1}{2} \mathbb{E}_{\mathbf{x} \sim p_{\text{data}}(\mathbf{x})} \left[ \|\mathbf{s}(\mathbf{x})\|_2^2 \right]}_{C} \end{align*}\]

Stationarity from the Magnitude Term

Loss funciton \(\tilde{\mathcal{L}}_{\text{SM}}(\phi)\)의 첫번쨰 항인 \(\dfrac{1}{2} \|\mathbf{s}_{\phi}(\mathbf{x})\|_2^2\)는 모델의 score의 크기를 0으로 만드는 역할을 한다. (\(\mathbf{s}_{\phi}(\mathbf{x}) \rightarrow 0\)) 이 항은 \(p_{\text{data}}(\mathbf{x})\)에 대한 기대값 안에 포함되어 있어 데이터 밀도가 높은 영역 (High density region)에서 더 강력하게 작용한다. 즉 데이터가 많이 존재하는 곳에서는 Score(gradient 역할)은 0으로 수렴하게 되어 입자가 더 이상 이동하지 않고 머무르게 하는 stationary point를 형성한다.

Concavity When the Field is (Approximately) a Gradient

Loss funciton \(\tilde{\mathcal{L}}_{\text{SM}}(\phi)\)의 두번쨰 항인 \(Tr(\nabla_\mathbf{x} \mathbf{s}_\phi (\mathbf{x}))\)을 최소화한다는 것은 벡터장이 발산(Divergence)를 Negative로 만든다는 것이다. 즉 한 점으로 모이는 수렴(Sink)역할을 유도한다.

기하학적으로는 어떤 potential \(u\)에 대한 scalar function \(u: \mathbb{R}^D \rightarrow \mathbb{R}\)이 존재하고 \(\mathbf{s}_\phi = \nabla_\mathbf{x} u\)라고 가정해보자.

• Jacobian은 Hessian이 된다. (\(\nabla_\mathbf{x} \mathbf{s}_\phi = \nabla^2_\mathbf{x} u\))
• Divergence는 Hessian의 trace가 된다. (\(\nabla_\mathbf{x} \cdot \mathbf{s}_\phi (\mathbf{x}) = Tr(\nabla^2_\mathbf{x} u(\mathbf{x}))\))

데이터가 존재하는 정지점(stationary point, \(\mathbf{x}_*\))에서 taylor expansion을 수행하면 1차항은 \(\mathbf{s}_\phi (\mathbf{x}_*) = \nabla_{\mathbf{x}_*} u(\mathbf{x}_*) = \mathbf{0}\)이 되고, 2차항인 Hessian이 지배적인 항이 된다. 이 때 \(Tr(\nabla_\mathbf{x} \mathbf{s}_\phi (\mathbf{x}))\)가 음수가 되도록 학습하므로 해당 지점이 모든 방향에서 위로 볼록(Concave)한 형태, 즉 극대점(Local minimum)이 된다.

요약하자면: Score matching은 데이터가 있는 곳(정상)은 평평하게(Stationary) 만들고, 그 주변은 정상을 향해 모여들도록 산처럼 위로 볼록한(Concave) 형태를 띠게 만드는 과정이다.

Sampling with Langevin Dynamics

이렇게 구한 Score ($\mathbf{s}_{\phi^x})$를 가지고 추론할 때 Dontinous-time Langevin Dynamics를 적용하면 다음과 같다.

\[\begin{equation} \mathbf{x}_{n+1} = \mathbf{x}_{n} + \eta \mathbf{s}_{\phi^x} (\mathbf{x}_n) + \sqrt{2\eta} \mathbf{\epsilon}_n, \quad \mathbf{\epsilon}_n \sim \mathcal{N}(\mathbf{0}, \mathbf{I}) \end{equation}\]

이를 Continous-time Langevin SDE형태로 작성하면 다음과 같다. Dontinous-time Langevin Dynamics는 Continous-time Langevin SDE에 the Euler–Maruyama discretization을 적용한 형태라고 보면 된다.

\[\begin{equation} d\mathbf{x} = \eta \mathbf{s}_{\phi^x} (\mathbf{x}(t)) dt + \sqrt{2}d \mathbf{w} (t) \end{equation}\]

Denoising Score Matching

Sliced Score Matching and Hutchinson’s Estimator

\(\begin{equation*} \tilde{\mathcal{L}}_{\text{SM}}(\phi) = \mathbb{E}_{\mathbf{x} \sim p_{\text{data}}(\mathbf{x})} \left[ Tr(\nabla_\mathbf{x} \mathbf{s}_\phi (\mathbf{x})) + \dfrac{1}{2} \|\mathbf{s}_{\phi}(\mathbf{x})\|_2^2 \right] \end{equation*}\)

이 Loss function은 기존 \(\mathcal{L}_{\text{SM}}(\phi)\)보다는 tractable하나 앞서 언급한 것처럼 trace of Jacobian인 \(Tr(\nabla_\mathbf{x} \mathbf{s}_\phi (\mathbf{x}))\)이 quadratic하다는 것이 문제였다. 이를 해결하기 위해 모든 차원의 Jacobian이 아닌 단면만 보고 1차원적인 기울기를 통해 trace 항을 대체한다.

만약 \(D\)차원에서 isotropic random vector \(\mathbf{u} \in \mathbb{R}^D\)가 존재한다고 가정하자. (Rademacher나 standard Gaussian이면 된다.) 이 때 \(\mathbb{E} [\mathbf{u}] = 0\)고 \(\mathbb{E} [\mathbf{u} \mathbf{u}^{\mathsf{T}}]= \mathbf{I}\)를 만족한다.

이 경우 Hutchinson’s identity는 다음을 만족한다.

\[\begin{align} Tr(A) &= \mathbb{E}_\mathbf{u} [ \mathbf{u}^\mathsf{T} \mathbf{A} \mathbf{u}] \\ \mathbb{E}_\mathbf{u} [(\mathbf{u}^\mathsf{T} \mathbf{s}_\phi(\mathbf{x}))^2] &= \| \mathbf{s}_\phi (\mathbf{x}) \|^2_2 \end{align}\]

그러면 기존 Loss function에서 trace term은 대체가 되고 다음과 같이 다시 쓸 수 있다.

\[\begin{equation*} \tilde{\mathcal{L}}_{\text{SM}}(\phi) = \mathbb{E}_{\mathbf{x}, \mathbf{u}} \left[ \mathbf{u}^\mathsf{T} (\nabla_\mathbf{x} \mathbf{s}_\phi (\mathbf{x}))\mathbf{u} + \dfrac{1}{2} (\mathbf{u}^\mathsf{T} \mathbf{s}_{\phi}(\mathbf{x}) )^2 \right] \end{equation*}\]

이렇게 변형된 Loss function은 \(\mathbf{J}\)를 Jacobian을 전부 계산하는 것이 아닌 결합법칙을 사용하여 Jacobian-vector-product 혹은 Vector-Jacboian-product 형태로 행렬과 벡터의 곱으로 효과적으로 계산한다. 이는 랜덤한 방향에서의 모델의 변화량 혹은 움직임을 보는 것으로 데이터 포인트에서는 loss가 stationary하게 유지될 것이다. 그러나, low manifolds에 이미지가 의존하게 되어 벡터 필드 score가 불안정하게 될 가능성이 높다. 즉, sliced score matching으로는 data point 근처에서 concave를 유지하게 만드는 constraint가 없다. 또한, Jacobian을 통으로 계산하는 것보단 낫지만 JVP/VJP를 통해 여러번 행렬-벡터 연산을 수행하면서 계산이 많아지고 variance가 생기는 문제도 있다. 이를 해결하기 위해 Denoising Score Matching이 등장하게 된다.

Training

[4]에서는 Denosing Score Matching을 통해 이론적으로 principled하고 현실적으로도 robust하고 scalable한 솔루션을 제공하고자 했다.

DSM은 Loss function을 원점에서 다시 생각한다.

\[\begin{align} \mathcal{L}_{SM} (\phi) &=\dfrac{1}{2} \mathbb{E}_{p_{\textrm{data}}(\mathbf{x})} \|\mathbf{s}_\phi (\mathbf{x})- \nabla_\mathbf{x} p_{\textrm{data}} (\mathbf{x})\|^2_2 \end{align}\]

여기서 맨 처음 문제가 되었던건 \(\nabla_\mathbf{x} p_{\textrm{data}} (\mathbf{x})\) 이 항이 intractable하다는 것이다.

Vincent’s Solution by Conditioning

Vincent는 이 문제를 scale \(\sigma\)를 따르는 조건부 분포(known) \(p_\sigma (\tilde{\mathbf{x}} \mid \mathbf{x})\)를 도입하여 데이터 \(\mathbf{x} \sim p_{data}\)에 노이즈를 주입하는 방식을 제안했다.

이 때 신경망 \(p_\sigma (\tilde{\mathbf{x}})\)은 다음과 같이 정의되는 marginal perturbed distribution의 score을 근사하도록 gkrtmqgksek.

\[p_\sigma (\tilde{\mathbf{x}}) = \int p_\sigma (\tilde{\mathbf{x}} \mid \mathbf{x}) p_{data} (\mathbf{x}) d \mathbf{x}\]

따라서 최소화할 Loss는 다음과 같다.

\[\begin{align} \mathcal{L}_{SM} (\phi; \sigma) := \dfrac{1}{2} \mathbb{E}_{\tilde{\mathbf{x}} \sim p_\sigma} \left[ \|\mathbf{s}_\phi (\tilde{\mathbf{x}};\sigma) - \nabla_\tilde{\mathbf{x}} \log p_\sigma (\tilde{\mathbf{x}})\|^2_2 \right] \end{align}\]

그냥 단순히 \(\sigma\)와 \(\tilde{\mathbf{x}}\)를 도입한 것에 지나지 않아 \(\nabla_\tilde{\mathbf{x}} \log p_\sigma (\tilde{\mathbf{x}})\)가 여전히 intractable하지만, Vincent는 결국 \(\mathbf{x} \sim p_{data}\)에 conditioning을 추가하면 다음과 같은 Loss가 되고 이는 위의 Loss와 동일하다는 것을 보였다.

\[\begin{align} \mathcal{L}_{DSM} (\phi; \sigma) := \dfrac{1}{2} \mathbb{E}_{\mathbf{x} \sim p_{data}, \tilde{\mathbf{x}} \sim p_\sigma (\cdot \mid \mathbf{x})} \left[ \|\mathbf{s}_\phi (\tilde{\mathbf{x}};\sigma) - \nabla_\tilde{\mathbf{x}} \log p_\sigma (\tilde{\mathbf{x}} \mid \mathbf{x})\|^2_2 \right] \end{align}\]

이렇게 구해서 최적화된 신경망 (optimal minimizer) \(\mathbf{s}^*\)은 conditioning을 처음 도입했을 때 신경망이 도달하고자 했던 목표 \(\nabla_\tilde{\mathbf{x}} \log p_\sigma (\tilde{\mathbf{x}})\)가 된다.

\[\begin{equation} \mathbf{s}^* (\tilde{\mathbf{x}}; \sigma) = \nabla_{\tilde{\mathbf{x}}} \log p_\sigma (\tilde{\mathbf{x}}) \end{equation}\]

Equivalence of \(\mathcal{L}_{SM}\) and \(\mathcal{L}_{DSM}\)

위 내용을 formalize하면 다음과 같다.

어떤 고정된 noise scale \(\sigma > 0\)에 대해서 다음을 만족한다.

\[\begin{equation} \mathcal{L}_{SM} (\phi ; \sigma) = \mathcal{L}_{DSM} (\phi ; \sigma) + C \end{equation}\]

이 떄 $C$는 파라미터 $\phi$와 무관한 상수이며 두 Loss가 만드는 minimizer \(s^*(\cdot ; \sigma\)는 다음과 같다.

\[\begin{equation} \mathbf{s}^* (\tilde{\mathbf{x}}; \sigma) = \nabla_{\tilde{\mathbf{x}}} \log p_\sigma (\tilde{\mathbf{x}}), \quad \text{for almost every } \tilde{\mathbf{x}} \end{equation}\]

증명은 각 MSE Loss를 전개하면 $\phi$관련된 term은 소거되고 관련없는 term만 $C$로 남게 된다.

이를 통해 DDPM부터 내려온 다음과 같은 테크닉을 알 수 있다.

데이터 포인트 $\mathbf{x}$에 대해 conditioning을 사용해서 intractable한 loss를 tractable한 loss로 바꾼다. (MOnte Carlo Estimation 대상)

Special Case: Additive Gaussian Noise

Reference

1. [1]C.-H. Lai, Y. Song, D. Kim, Y. Mitsufuji, and S. Ermon, “The Principles of Diffusion Models,” arXiv preprint arXiv:2510.21890, 2025.
2. [2]Y. Song, J. Sohl-Dickstein, D. P. Kingma, A. Kumar, S. Ermon, and B. Poole, “Score-based generative modeling through stochastic differential equations,” arXiv preprint arXiv:2011.13456, 2020.
3. [3]A. Hyvärinen and P. Dayan, “Estimation of non-normalized statistical models by score matching.,” Journal of Machine Learning Research, vol. 6, no. 4, 2005.
4. [4]P. Vincent, “A connection between score matching and denoising autoencoders,” Neural computation, vol. 23, no. 7, pp. 1661–1674, 2011.