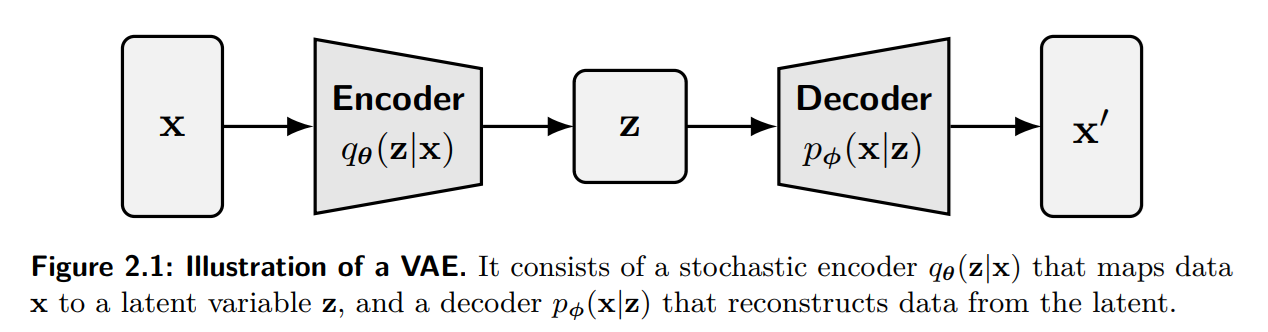
From VAEs to DDPMs
Introduction
최근에 올라온 이 책 저자가 저자라 그런지 너무나도 깔끔하고 아름답다. [1]
따라서 한번 챕터별로 정리하면서 읽어보려고 한다. 특히 현재 챕터는 다음 글이 같이 떠올랐고 같이 읽어보면 좋을 것 같다. [2]
Review of Bayesian Inference
베이즈 추론(Bayesian Inference)에서 훈련과 추론(예측)은 모두 베이즈 정리를 기반으로 하지만, 초점과 입출력이 다르다.
- 훈련(Training): 데이터 $\mathcal{D}$을 사용해 모델의 파라미터 $\theta$에 대한 믿음을 업데이트(추론)
- 추론(Inference): 업데이트된 믿음을 사용해 새로운 데이터 $\mathcal{D}_{new}$를 예측하는 과정
Bayes Rule
관찰된 결과(Data)를 바탕으로 관찰되지 않은 원인(Parameter)을 추론하는 것
- 원인: $\theta$
- 알고자 하는 목표
- 모델의 파라미터, 시스템의 hidden state 등
- 결과: $\mathcal{D}$
- 관찰한 것
- 실험 결과, 수집된 데이터 샘플
Posterior:
\[P(\theta \mid \mathcal{D})\]- (원인 $\mid$ 결과)
- 정의: 결과($\mathcal{D}$)를 관찰했을 때, 이 현상의 원인이 $\theta$일 확률.
- 의미:
- 데이터를 본 후 업데이트된 믿음 또는 지식
- 훈련의 최종 목표
Likelihood:
\[P(\mathcal{D} \mid \theta)\]- (결과 $\mid$ 원인)
- 정의: 원인이 $\theta$라고 가정할 때, 관찰한 결과($\mathcal{D}$)가 나타날 확률.
- 의미:
- 특정 파라미터($\theta$)가 주어진 데이터를 얼마나 잘 설명하는지를 나타내는 값
- 데이터가 모델에 적합한 정도를 측정
- Prior
- (원인)
- 정의: 결과($\mathcal{D}$)를 관찰하기 전에, 원인이 $\theta$일 것이라고 믿는 초기 확률
- 의미:
- 데이터와 무관하게 우리가 이미 가지고 있는 사전 지식이나 가정
- Evidence
- (결과)
- 정의: 우리가 관찰한 결과($\mathcal{D}$)가 나타날 총 확률
- 의미:
모든 가능한 원인($\theta$)에 대해 가중 평균을 낸 값
\[P(\mathcal{D}) = \int P(\mathcal{D} \mid \theta) P(\theta) d\theta\]- 실제로는 Posterior를 확률 분포로 만들기 위한 정규화 상수
- 계산이 매우 어려워 MCMC 같은 샘플링 기법을 사용하여 계산
훈련 (Training)
데이터($\mathcal{D}$)를 사용해 파라미터($\theta$)의 사후 확률 분포($P(\theta \mid \mathcal{D})$)를 찾는 과정
- 목표: 데이터가 주어졌을 때, 모델 파라미터($\theta$)가 어떠한 분포를 따르는지 알아내는 과정
- $P(\theta \mid \mathcal{D})$를 구하는 것
- 입력 (Inputs):
- 데이터 (Data): $\mathcal{D}$
- 사전 확률 (Prior): $P(\theta)$ (우리가 $\theta$에 대해 미리 가정한 분포)
- 가능도 함수 (Likelihood Model): $P(\mathcal{D} \mid \theta)$ (데이터 생성 과정을 정의하는 모델)
- 과정 (Process):
- 베이즈 정리를 적용: $P(\theta \mid \mathcal{D}) \propto P(\mathcal{D} \mid \theta) P(\theta)$ (참고: $P(\mathcal{D})$는 $\theta$에 대해 상수이므로 비례 관계로 표현)
- 실제로는 $P(\mathcal{D})$ 계산이 어렵거나 $P(\theta \mid \mathcal{D})$가 복잡한 형태일 경우, MCMC(Markov Chain Monte Carlo)나 변분 추론(Variational Inference) 같은 근사(approximation) 방식을 사용해 $P(\theta \mid \mathcal{D})$에서 샘플을 추출하거나 근사 분포를 찾습니다.
- 출력 (Output):
- 사후 확률 분포 (Posterior Distribution): $P(\theta \mid \mathcal{D})$
- 단일 값이 아닌, $\theta$가 가질 수 있는 값들에 대한 확률 분포.
- (예: $\theta$는 95% 확률로 [2.5, 3.5] 사이에 있다.)
- 단일 값이 아닌, $\theta$가 가질 수 있는 값들에 대한 확률 분포.
- 사후 확률 분포 (Posterior Distribution): $P(\theta \mid \mathcal{D})$
추론 (Inference)
훈련을 통해 얻은 사후 확률 분포($P(\theta \mid \mathcal{D})$)를 사용해, 아직 보지 못한 새로운 데이터($\mathcal{D}_{new}$)가 어떨지 예측하는 과정
- 목표: 이미 관찰한 데이터 $\mathcal{D}$를 바탕으로, 새로운 데이터 \(\mathcal{D}_{new}\)의 분포인 사후 예측 분포(\(P(\mathcal{D}_{new} \mid \mathcal{D})\))를 구하기
- 입력 (Inputs):
- 사후 확률 분포 (Posterior): $P(\theta \mid \mathcal{D})$ (훈련 단계의 출력)
- 가능도 함수 (Likelihood Model): $P(\mathcal{D}_{new} \mid \theta)$ (새로운 데이터를 생성할 모델)
- (필요시) 새로운 입력값 (New Input): $x_{new}$ (예: \(\mathcal{D}_{new} = y_{new}\)를 예측하기 위한 $x_{new}$)
- 과정(Posterior Predictive Distribution)
- $\theta$ 값을 하나로 확정한다면, $P(\mathcal{D}_{new} \mid \theta)$이 고정된 예측값
- 베이즈 추론에서는 $\theta$가 $P(\theta \mid \mathcal{D})$라는 ‘분포’를 가짐 ($\theta$ 값에 불확실성이 존재)
- 가능한 모든 $\theta$ 값에 대해 예측(\(P(\mathcal{D}_{new} \mid \theta)\))을 수행하고 이를 해당 $\theta$가 맞을 확률($P(\theta \mid \mathcal{D})$)로 가중 평균
- 출력
- 사후 예측 분포 (Posterior Predictive Distribution): $P(\mathcal{D}_{new} \mid \mathcal{D})$
- $\mathcal{D}_{new}$에 대한 예측을 확률 분포로 제공
- 예: “새로운 환자의 생존 확률은 70%”가 아니라, “생존 확률은 95% 신뢰구간으로 [0.65, 0.75] 사이에 있다”처럼 예측의 불확실성(uncertainty)까지 포함
| 구분 | 1. 훈련 (Training / Parameter Inference) | 2. 추론 (Inference / Prediction) |
|---|---|---|
| 목적 | 데이터($\mathcal{D}$)를 통해 파라미터($\theta$)의 분포를 학습 | 학습된 파라미터 분포를 사용해 새 데이터($\mathcal{D}_{new}$) 예측 |
| 핵심 질문 | “데이터를 보니, 모델 파라미터($\theta$)는 무엇일까?” | “지금까지의 데이터와 모델을 보니, 다음 데이터($D_{new}$)는 어떨까?” |
| 주요 수식 | Posterior $P(\theta \mid \mathcal{D}) \propto P(\mathcal{D} \mid \theta) P(\theta)$ | Posterior Predictive \(P(\mathcal{D}_{new} \mid \mathcal{D}) = \int P(\mathcal{D}_{new} \mid \theta) P(\theta \mid \mathcal{D}) d\theta\) |
| 입력 (Input) | * Data ($\mathcal{D}$) * Prior ($P(\theta)$) * Likelihood ($P(\mathcal{D} \mid \theta)$) | * Posterior ($P(\theta \mid \mathcal{D})$) (훈련의 결과물) * Likelihood ($P(\mathcal{D}_{new} \mid \theta)$) |
| 출력 (Output) | Posterior Distribution $P(\theta \mid \mathcal{D})$ (파라미터 $\theta$에 대한 확률 분포) | Posterior Predictive Distribution \(P(\mathcal{D}_{new} \mid \mathcal{D})\) (새 데이터 $\mathcal{D}_{new}$에 대한 확률 분포) |
Deep Generative Modeling (DGM)
생성모델은 고차원 데이터로부터 확률 분포를 학습하여 데이터셋과 유사한 새로운 샘플을 생성해 내는 것이다.
훈련 데이터 분포를 $p_{\text{data}}$라고 하고, 모델의 확률분포를 $p_\phi (x)$라고 가정하자. 이 떄 모델의 파라미터 $\phi$를 훈련하여 $p_{\text{data}}$를 $p_\phi (x)$에 근사하게 만드는것이 생성모델의 목표이다. 두 분포가 얼마나 멀리 떨어져있는가? (KL Divergence 등) 를 측정하는것이 loss function의 역할을 하게 된다.
\[\begin{equation} p_{\phi^*} (\mathbf{x}) \approx p_{\text{data}} (\mathbf{x}) \end{equation}\]Training DGM
모델 family $\lbrace p_{\phi} \rbrace$는 discrepancy $\mathcal{D} (p_{\text{data}}, p_\phi)$
\[\begin{equation} \phi^* \in \mathop{\arg\min}\limits_{\phi} \mathcal{D} (p_{\text{data}}, p_\phi) \end{equation}\]이 때 $p_{\text{data}}$는 알 수 없는 값이므로, 데이터로부터 i.i.d. samples을 뽑아서 추정한다.
KL Divergence
$\mathcal{D} (p_{\text{data}}, p_\phi)$ ($p_\phi$로 $p_{\text{data}}$를 모델링할 때 잃어버리는 정보량) 로 가장 많이 쓰이는 것이 KL Divergence이다.
\[\begin{align} \mathcal{D}_{\mathrm{KL}}(p_{\text{data}} \| p_{\phi}) &:= \int p_{\text{data}}(\mathbf{x}) \log \frac{p_{\text{data}}(\mathbf{x})}{p_{\phi}(\mathbf{x})} \, d\mathbf{x} \\ &= \mathbb{E}_{\mathbf{x} \sim p_{\text{data}}} \left[ \log p_{\text{data}}(\mathbf{x}) - \log p_{\phi}(\mathbf{x}) \right]. \end{align}\]하지만 forward KL \(\mathcal{D}_{\mathrm{KL}}(p_{\text{data}} \| p_{\phi})\)를 최소화하는 과정은 모드 커버링(mode covering)이라는 생성하게 된다. 이는, 데이터가 존재하는 영역 $p_{\text{data}} > 0$이지만, 모델이 그 영역에 확률을 주지 않으면 $p_{\phi}(\mathbf{x}) = 0$이 되고
\(\begin{equation*} \log \frac{p_{\text{data}}(\mathbf{x})}{p_{\phi}(\mathbf{x})} = + \infty \end{equation*}\) 가 되어 KL이 무한대가 되기 때문에 데이터가 존재하는 모든 영역에 확률을 주려고 한다.
그러나 반대로 reverse KL \(\mathcal{D}_{\mathrm{KL}}(p_{\phi} \| p_{\text{data}} )\)에서는 데이터가 존재하는 일부 영역을 놓쳐도 큰 손해가 나지 않아 페널티가 크지 않다. 이를 큰 모드에 집중하는 mode seeking 이라고 한다.
또한 $p_{\text{data}}$는 직접 구할 수 없으므로 forward KL은 다음과 같이 쓸 수 있다. 이 떄, \(\mathcal{H}(p_{\text{data}}) := - \mathbb{E}_{\mathbf{x} \sim p_{\text{data}}}\)는 데이터의 entropy이다.
\[\begin{align} \mathcal{D}_{\mathrm{KL}}(p_{\text{data}} \| p_{\phi}) &= \mathbb{E}_{\mathbf{x} \sim p_{\text{data}}} \left[ \log \frac{p_{\text{data}}(\mathbf{x})}{p_{\phi}(\mathbf{x})} \right] \\ &= - \mathbb{E}_{\mathbf{x} \sim p_{\text{data}}} \left[ \log p_{\phi}(\mathbf{x}) \right] + \mathcal{H}(p_{\text{data}}), \end{align}\]즉 KL을 최소화하는 것은 MLE와 같은 말이다.
\[\begin{align} \min_{\phi} \, \mathcal{D}_{\mathrm{KL}}(p_{\text{data}} \| p_{\phi}) \;\Longleftrightarrow\; \max_{\phi} \, \mathbb{E}_{\mathbf{x} \sim p_{\text{data}}} \left[ \log p_{\phi}(\mathbf{x}) \right]. \end{align}\]Variational Autoencoder(VAE)
기존의 Autoencoder는 고정된 latent vector가 있지만, VAE에서는 latent vector를 확률 분포로 만들어 generative model로 만들어버림
Probabilistic Encoder and Decoder
Construction of Decoder (Generator)
- $\mathbf{x}$: 관찰된 변수. 우리가 보는 이미지
- $\mathbf{z}$: 잠재 변수 (latent variable). 이미지에 숨겨진 feature
- 가정:
- 가우시안 같은 단순한 prior 분포($\mathbf{z} \sim p_{\text{prior}} := \mathbf{\mathcal{N}(0, I)}$)로부터 $\mathbf{x}$를 생성
- $\mathbf{x}$와 $\mathbf{z}$의 생성
- Decoder 분포를 $p_\theta(\mathbf{x} \mid \mathbf{z})$라고 했을때,
- Sampling: $\mathbf{z} \sim p_{\text{prior}}$
- Decoding: $\mathbf{x} \sim p_\theta(\mathbf{x} \mid \mathbf{z})$
VAE는 다음과 같은 marignal likelihood에 의해 latent-variable generative model로 정의된다. 이게 $p_\theta(\mathbf{x} \mid \mathbf{z})$는 $z$라는 원인으로부터 $x$가 생성(결과)이므로 (결과 $\mid$ 원인)인 likelihood이기 때문이다.
\[\begin{equation} p_\phi (x) = \int p_\phi(\mathbf{x} \mid \mathbf{z}) p(\mathbf{z}) d\mathbf{z} \end{equation}\]이상적으로는 decoder 파라미터 $\phi$는 marignal likelihood를 최대화해서 학습할 수 있지만. $p(\mathbf{z})$를 구하기가 힘들다.
왜냐하면 $\mathbf{z}$가 $m$개의 변수라고 하고, 각 변수마다 $n$개씩 쪼개서 계산한다 하더라도 $m \times n$이라는 엄청난 수의 grid point가 필요하기 때문이다. 따라서 이를 변수를 바꿔서 계산(변분법)하게 된다.
Construction of Encoder (Inference Network)
반대로 $\mathbf{x}$로 부터 $\mathbf{z}$를 생성하기 위해서는 $p_\theta(\mathbf{z} \mid \mathbf{x})$가 필요하고 베이즈 정리에 따라 다음과 같이 계산한다.
\[\begin{equation*} p_\phi(\mathbf{z} \mid \mathbf{x}) = \dfrac{p_\phi(\mathbf{x} \mid \mathbf{z}) p(\mathbf{z})}{p(\mathbf{x})} \end{equation*}\]Decoder와 마찬가지로 $p(\mathbf{x})$를 일반적인 계산으로 구하기 어렵다. (intractable) 즉, $\mathbf{x}$로부터 $\mathbf{z}$를 구하는 것은 불가능하다.
따라서, intractable posterior를 tractable approximation으로 교체하는 것이 필수적이며 이걸 변분법적 접근이라고 한다. Encoder 네트워크 $q_\theta(\mathbf{z} \mid \mathbf{x})$를 가정해서 다음과 같이 정의하자.
\[\begin{equation*} q_\theta(\mathbf{z} \mid \mathbf{x}) \approx p_\phi(\mathbf{z} \mid \mathbf{x}) \end{equation*}\]여기서 $q_\theta(\mathbf{z} \mid \mathbf{x})$는 근사 사후 확률(Approximate Posterior)가 된다.
즉 Decoder는 Likelihood $\phi_\phi(x \mid z)$를, Encoder는 Approximate posterior $q_\theta(z \mid x)$를 훈련한다.
Training via the Evidence Lower Bound (ELBO)
지금까지 내용을 정리해보자면, 생성 모델인 모델이 얼마나 데이터 $x$를 잘 설명하는가?이고, 이는 데이터의 가능도 $\log p_\phi(\mathbf{x})$를 최대화하여 이루어진다. 그러나, VAE에서는 $\log p_\phi(\mathbf{x})$를 직접 구하려면 모든 $\mathbf{z}$에 대해 구해야해서 어렵다.
- VAE(생성 모델)의 목표: Marginal Likelihood $\log p_\phi(\mathbf{x})$의 최대화
- 필요한 것: $p (\mathbf{z} \mid \mathbf{x})$
- 문제점:
- $p_\phi (x) = \int p_\phi(\mathbf{x} \mid \mathbf{z}) p(\mathbf{z}) d\mathbf{z}$의 모든 $\mathbf{z}$에 대해서 구하는건 불가능
- $\mathbf{z}$에 대해 샘플링해서 구하자니 효율적으로 샘플링하지 않으면 대부분 0이 나올 가능성이 높음
- $\mathbf{x}$가 주어졌을때 $\mathbf{x}$를 만들었을 $\mathbf{z}$의 분포 $p(\mathbf{z} \mid \mathbf{x})$가 필요
- \[p_\phi (\mathbf{z} \mid \mathbf{x}) = \frac{p_\phi(\mathbf{x} \mid \mathbf{z}) p(\mathbf{z})}{p(\mathbf{x})}\]
- $p(\mathbf{x})$를 알아야함
- 목표로 다시 회귀. $\log p_\phi(\mathbf{x})$를 구할 수가 없음
- 해결책
- True \(p_\phi (\mathbf{z} \mid \mathbf{x})\)는 찾을 수 없음
- \(q_\theta (\mathbf{z} \mid \mathbf{x}) \approx p_\phi (\mathbf{z} \mid \mathbf{x})\)를 훈련하여 $q_\theta (z \mid x)$를 사용하자 (Variational Inference)
- 즉 $\log p_\phi(\mathbf{x})$를 최대화를 변수를 바꿔서 (변분 추론, Varaitional Inference)를 통해서 \(q_\theta (z \mid x)\)를 사용하자.
이렇게 된것이다. 여기서 ELBO가 나오게 된다.
Deriving ELBO
우리의 목표는 \(p_\phi (\mathbf{z} \mid \mathbf{x})\)와 근사한 \(q_\theta (z \mid x)\)를 찾는 것이다. 또한 $p_\phi (\mathbf{z})$를 $q_\theta (z \mid x)$로 변수를 바꾸는 것이 목표이다. 즉, 기존의 $\log p_\phi(\mathbf{x})$를 $q_\theta (z \mid x)$에 대해서 표현하는 것이다.
\[\begin{equation*} p_\phi (\mathbf{z} \mid \mathbf{x}) = F \left( q_\theta (z \mid x) \right) \end{equation*}\]이러면 $q_\theta (z \mid x)$에 대해 $\log p_\phi(\mathbf{x})$를 평균내어도 원래의 $\log p_\phi(\mathbf{x})$를 얻을 수 있어야 한다.
\[\begin{align*} \log p_\phi(\mathbf{x}) &= \log \int p_\phi(\mathbf{x,z}) d\mathbf{z}\\ &=\log \int q_\theta (z \mid x) \dfrac{p_\phi(\mathbf{x,z})}{q_\theta (z \mid x)} d\mathbf{z} \\ &= \log \mathbb{E}_{\mathbf{z} \sim q_\theta (z \mid x)} \left[ \dfrac{ p_\phi(\mathbf{x,z})}{q_\theta (z \mid x)} \right] \\ &\geq \mathbb{E}_{\mathbf{z} \sim q_\theta (z \mid x)} \left[ \log \left( \dfrac{p_\phi(\mathbf{x, z})}{q_\theta (z \mid x)} \right) \right] \\ &\equiv \mathcal{L} (\phi, \theta ; \mathbf{x}) \; \text{(ELBO)} \end{align*}\]여기서 나온 ELBO는 다음과 같이 분해된다.
\[\begin{align*} \mathcal{L} (\phi, \theta ; \mathbf{x}) &= \mathbb{E}_{\mathbf{z} \sim q_\theta (z \mid x)} \left[ \log \left( \dfrac{p_\phi(\mathbf{x, z})}{q_\theta (z \mid x)} \right) \right] \\ &= \mathbb{E}_{\mathbf{z} \sim q_\theta (z \mid x)} \left[ \log p_\phi(\mathbf{x, z}) - \log q_\theta (z \mid x) \right] \\ &= \mathbb{E}_{\mathbf{z} \sim q_\theta (z \mid x)} \left[ \log p_\phi(\mathbf{x \mid z})p_\phi(\mathbf{z}) - \log q_\theta (z \mid x) \right] \\ &= \mathbb{E}_{\mathbf{z} \sim q_\theta (z \mid x)} \left[ \log p_\phi(\mathbf{x \mid z}) + \log p_\phi(\mathbf{z}) - \log q_\theta (z \mid x) \right] \\ &= \underbrace{\mathbb{E}_{\mathbf{z} \sim q_\theta (z \mid x)} \left[ \log p_\phi(\mathbf{x \mid z}) \right]}_{\text{Reconstruction Term}} + \underbrace{\mathbb{E}_{\mathbf{z} \sim q_\theta (z \mid x)} \left[ \log p_\phi(\mathbf{z}) - \log q_\theta (z \mid x) \right]}_{\text{Latent Regularization}} \\ &= \underbrace{\mathbb{E}_{\mathbf{z} \sim q_\theta (z \mid x)} \left[ \log p_\phi(\mathbf{x \mid z}) \right]}_{\text{Reconstruction Term}} - \underbrace{ \mathcal{D}_{KL} (q_\theta (z \mid x) \| p(\mathbf{z}))}_{\text{Latent Regularization}} \\ \end{align*}\]이 때 ELBO는 두 가지 term으로 구성된다.
- Reconstruction (디코더 $z -> x$)
- \[\mathbb{E}_{\mathbf{z} \sim q_\theta (z \mid x)} \left[ \log p_\phi(\mathbf{x \mid z}) \right]\]
- 방향: $\mathbf{z} \rightarrow \mathbf{x}$ (Decoder, 생성)
- 목표: 데이터 충실도 (Data Fidelity). 즉, $z$로부터 원본 $x$를 얼마나 잘 복원하는가?
- 최대화가 목표 (그래서 +)
- 디코더 출력 분포 $p_\phi (\mathbf{x} \mid \mathbf{z})$가 실제 데이터 분포 \(p_{\text{data}} (\mathbf{x})\) (입력 $x$로 대표됨)을 모델링할 떄의 비용
- \[D_{KL}(p_{\text{data}} (\mathbf{x}) || p_\phi (\mathbf{x} \mid \mathbf{z}))\]
- Latent KL (인코더 $x -> z$)
- \[\mathcal{D}_{KL} (q_\theta (z \mid x) \| p(\mathbf{z}))\]
- 방향: $\mathbf{x} \rightarrow \mathbf{z}$ (Encoder, 압축/추론)
- 목표: 잠재 공간 정규화. 즉, 인코더가 $z$를 $x$로 매핑할 때, 그 $z$의 분포가 우리가 원하는 단순한 형태 (보통 Gaussian인 $p(x)$)를 따르도록 강제
- 최소화가 목표 (그래서 -)
- 단순한 사전 분포 $p(x)$가 인코더의 출력분포 $q_\theta (z \mid x)$를 모델링할 때의 비용
- \[D_{KL}(q_\theta (z \mid x) || p(x))\]
여기서 다음과 같이 Trade-off가 있다.
복원력에 초점을 두면 Reconstruction은 최대화할 수 있겠지만, 암기(memorization)에만 초점을 둬 \(q_\theta (z \mid x)\)가 뾰족해지고, Latent KL \(D_{KL}(q_\theta (z \mid x) || p(x))\)은 커지게된다. 반대로 잠재 공간을 너무 단순하게 만들면, \(q_\theta (z \mid x)\)와 \(p(x)\)가 같아진다고 볼 수 있고, 이는 인코더가 $x$의 정보를 $z$에 반영하지 않아 (독립) 디코더의 입장에서는 \(p_{\text{data}} (\mathbf{x})\)의 평균을 내놓게 될 뿐이다. 이로 인해 Reconstruction \(\mathbb{E}_{\mathbf{z} \sim q_\theta (z \mid x)} \left[ \log p_\phi(\mathbf{x \mid z}) \right]\)은 커지게 된다.
Blurry Generations in VAEs
VAE를 실제로 훈련하다보면 Blurry하게 생성되는 경우가 많다. 처음에는 Autoencoder보다 더 안좋은 결과 같아서 당황하지만, 알고보면 당연하다.
어떤 고정된 Gaussian encoder \(q_{enc} (\mathbf{z} \mid \mathbf{x})\)와 Gaussian Decoder \(p_{dec} (\mathbf{x} \mid \mathbf{z})\)가 있다고 하자. 이는 Encoder와 Decoder를 모두 생각해야하는 기존 VAE의 문제를 Decoder에만 집중하게만 해준다. 이 떄, \(p_{dec} (\mathbf{x} \mid \mathbf{z})\)은 Gussian 관점에서 다음과 같이 표현할 수 있다.
\[\begin{equation} p_{dec} (\mathbf{x} \mid \mathbf{z}) = \mathcal{N}(\mathbf{x} ; \mu(\mathbf{z}), \sigma^2 \mathbf{I}) \end{equation}\]이러면 \(p_{dec}\)를 Gaussian으로 고정했지만 \(\mu\)는 변할 수 있다. 그래서 $\mu(\mathbf{z})$은 autoencoder의 decoder와 비슷한 decoder network에 대응된다고 하자.
임의의 Encoder \(q_{enc} (\mathbf{z} \mid \mathbf{x})\)에서 ELBO를 최적화하는 것은 다음과 같은 Reconstruction Error을 최소화 하는 것과 같다. 왜냐하면 Latent KL \(\mathcal{D}_{KL} (q_\theta (z \mid x) \| p(\mathbf{z}))\)은 고정된 encoder \(q_\theta (z \mid x)\)와 고정된 prior $p(\mathbf{z})$로 인해 상수가 되기 때문이다.
\[\begin{equation} \mathop{\arg\min}\limits_{\mu} \mathbb{E}_{p_{\text{data}}, q_{enc} (\mathbf{z} \mid \mathbf{x})} \left[ \| \mathbf{x} - \mathbf{\mu} (\mathbf{z}) \|^2\right] \end{equation}\]이는 \(\mathbf{\mu} (\mathbf{z})\)에 대한 least square problem과 같고, 따라서 그 해는 다음과 같다. \(\begin{equation} \mathbf{\mu}^* (\mathbf{z}) = \mathbb{E}_{q_{enc} (\mathbf{x} \mid \mathbf{z})} [\mathbf{x}] \end{equation}\)
이 떄 중요한 것은 \(q_{enc} (\mathbf{x} \mid \mathbf{z})\)이라는 건데, 오타가 아니고 정말 \(x\)와 \(z\)의 방향이 바뀐 것이다. 이는 별도의 \(p_{dec} (\mathbf{x} \mid \mathbf{z})\)가 아닌 일종의 역함수처럼 \(q_{enc}\)의 방향을 뒤집은 것이고 다음과 같이 정의한다.
\[\begin{equation} q_{enc} (\mathbf{x} \mid \mathbf{z}) = \dfrac{q_{enc} (\mathbf{z} \mid \mathbf{x}) p_{\text{data}} (\mathbf{x})}{p_{\text{prior}} (\mathbf{z})} \end{equation}\]$\mathbf{\mu}^*$을 기대값의 형태로 풀어쓰고 여기에 다시 \(q_{enc} (\mathbf{x} \mid \mathbf{z})\)를 대입해서 정리해볼 수 있다. 참고로 베이즈 정리에 따른 적분식 $P(B) = \int P(B \mid A) P(A) dA$를 사용한다.
\[\begin{align*} \mathbf{\mu}^* (\mathbf{z}) &= \mathbb{E}_{q_{enc} (\mathbf{x} \mid \mathbf{z})} [\mathbf{x}] \\ &= \int \mathbf{x} \cdot q_{enc} (\mathbf{x} \mid \mathbf{z}) d\mathbf{x} \\ &= \int \mathbf{x} \cdot \dfrac{q_{enc} (\mathbf{z} \mid \mathbf{x}) p_{\text{data}} (\mathbf{x})}{p_{\text{prior}} (\mathbf{z})} d\mathbf{x} \\ &= \dfrac{1}{p_{\text{prior}} (\mathbf{z})} \int \mathbf{x} \cdot q_{enc} (\mathbf{z} \mid \mathbf{x}) p_{\text{data}} (\mathbf{x}) d\mathbf{x} \\ &= \dfrac{1}{\int q_{enc}(\mathbf{z} \mid \mathbf{x}) p_{\text{data}}(\mathbf{x}) d\mathbf{x}} \int \mathbf{x} \cdot q_{enc} (\mathbf{z} \mid \mathbf{x}) p_{\text{data}} (\mathbf{x}) d\mathbf{x} \\ &= \dfrac{1}{\mathbb{E}_{p_{\text{data}}} q_{enc} (\mathbf{z} \mid \mathbf{x})} \int \mathbf{x} \cdot q_{enc} (\mathbf{z} \mid \mathbf{x}) p_{\text{data}} (\mathbf{x}) d\mathbf{x} \\ &= \dfrac{1}{\mathbb{E}_{p_{\text{data}}} q_{enc} (\mathbf{z} \mid \mathbf{x})} \mathbb{E}_{p_{\text{data}}} [q_{enc} (\mathbf{z} \mid \mathbf{x})] \\ \end{align*}\]다시 정리하면 다음과 같이 표현된다.
\[\begin{equation} \mathbf{\mu}^* (\mathbf{z}) = \dfrac{\mathbb{E}_{p_{\text{data}}} [q_{enc} (\mathbf{z} \mid \mathbf{x}) \mathbf{x}]}{\mathbb{E}_{p_{\text{data}}} [q_{enc} (\mathbf{z} \mid \mathbf{x})]} \end{equation}\]만약 서로 다른 입력 \(\mathbf{x} \neq \mathbf{x}'\)이 있고, latent space에서 일부 겹친다고 가정하자. 예를 들어 \(q_{enc} (\cdot \mid \mathbf{x})\) 와 \(q_{enc} (\cdot \mid \mathbf{x'})\)의 support들이 서로 겹치는 것이다.
그 말은 $\mathbf{\mu}^* (\mathbf{z})$은 여러 입력을 평균내게되는데 (말 그대로 평균이니까) 이는 겹치는 구간에서는 서로 상관이 없어도 단순 평균을 낸다는 것이다. 따라서 상관없는 입력끼리 평균을 내버리면 blurry한 결과가 나오게 된다.
즉, L2 손실(Reconstruction Error)을 최소화하는 최적의 Decoder \(\mu^*(\mathbf{z})\)는 어떤 \(\mathbf{z}\)가 주어졌을 때, 그 \(\mathbf{z}\)를 만들었을 가능성이 있는 모든 원본 \(\mathbf{x}\)들의 ‘평균’을 출력하게 된다는 것이다.
Variational Perspective: DDPM
기존 책에는 HVAE와 왜 HVAE로도 기존 VAE의 문제를 완전히 해결하지 못하는지에 대한 이야기가 담겨있다. 요약하면 (1) Encoder의 문제: 깊은 모델이어도 결국 Encoder는 Gaussian으로 근사하고, multi-peaked인 경우에는 이를 모두 포함하기 위해 매우 loose한 Guassian으로 근사하게 된단 점, (2) Decoder의 문제: Decoder가 너무 강력해서 $\mathbf{z}$를 무시하게 되어 controllable하지 않다.라는 문제를 지적했다.
DDPM(Denoising Diffusion Probabilistic Models)은 이를 해결하기 위해 Encoder를 고정하고 Decoder만을 학습한다.
- The forward pass (Fixed Encoder):
- \(p(\mathbf{x}_i \mid \mathbf{x}_{i-1})\)이라는 transition kernel을 통해 데이터에 Gaussian noise를 서서히 주입하여 데이터를 왜곡한다.
- 결국 데이터는 isotropic Gaussian data로 전환되게 되고, 이 과정은 항상 일정하므로 고정된 Encoder라고 할 수 있다.
- The reverse Denoising Process (Learnables Decoder):
- Decoder에서는 parameterized된 \(p_{\phi}(\mathbf{x}_{i_1} \mid\mathbf{x}_{i})\)을 통해 노이즈 주입을 reverse하는 과정을 배우게 된다.
- VAE에서 한번에 denoising하는 것보다는 훨씬 더 controllable하다.
The forward pass (Fixed Encoder)
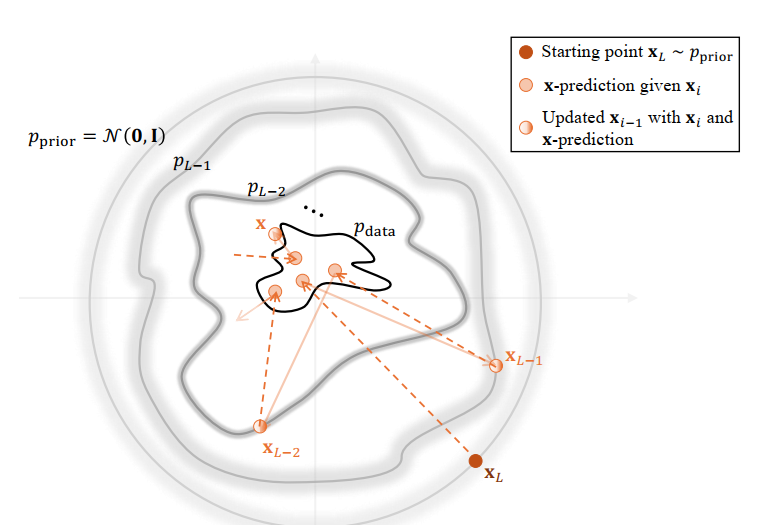
앞서 말했던 것처럼 forward process는 다음 그림과 같이 단계적으로 노이즈를 추가해서 심플한 prior $p_{\text{prior}} := \mathcal{N}(\mathbf{0, I})$으로 만드는 과정이다.
Fixed Gaussian Kernels
여기서 단계적이라는 말은 동적인 모델의 파라미터가 아닌 고정된 Gaussian Kernel에 의해 지배된다. 개인적으로 DDPM을 처음 접할 때 가장 헷갈리는 notation이 $;$과 $,$의 차이인데 우선 $;$는 확률변수와 파라미터를 구분할 때 쓴다. 아래의 식은 \(\mathbf{x}_{i-1}\)이 주어졌을 때 \(\mathbf{x}_i\)가 나타날 확률은, $x_i$를 확률 변수로 하고 (\(\sqrt{1-\beta_i^2} \mathbf{x}_{i-1}\))를 평균으로 \((\beta_i^2 \mathbf{I})\)를 공분산으로 갖는 정규분포를 따른다라는 의미를 가진다. 반면 뒤에 나오는 $,$는 확률 변수가 여러 개임을 뜻한다. 예를 들어 \(p (\mathbf{x}_{i-1} \mid \mathbf{x}_{i}, \mathbf{x}_0)\)는 \(\mathbf{x}_{i}, \mathbf{x}_0\) 두 확률변수가 주어졌을 때의 \(\mathbf{x}_{i-1}\)의 조건부 확률을 뜻한다.
\[\begin{align} p(\mathbf{x}_i \mid \mathbf{x}_{i-1}) := \mathcal{N}(\mathbf{x}_i ; \sqrt{1-\beta_i^2} \mathbf{x}_{i-1}, \beta_i^2 \mathbf{I}) \end{align}\]조금 더 디테일하게 설명하자면, 맨 처음에는 실제 데이터 분포 $p_{\text{data}}$로부터 샘플링된 $\mathbf{x}_0$부터 시작한다. 그리고 \(\lbrace \beta_i \rbrace_{i=1}^L\)는 서서히 증가하는 noise scheudle이다. $\beta_i \in \lbrace 0, 1 \rbrace$는 step $i$에 주입되는 Gaussian noise의 양을 결정한다. 만약 $\alpha_i := \sqrt{1-\beta^2}$라고 가정하면 다음과 같이 단순히 iterative하게 노이즈 주입하는 식인 것일 뿐이다.
\[\begin{align} \mathbf{x}_i = \alpha_i \mathbf{x}_{i-1} + \beta_i \mathbf{\epsilon}_i \end{align}\]이 때, $\mathbf{\epsilon}_i \sim \mathcal{N}(\mathbf{0}, \mathbf{I})$는 i.i.d.인 noise이다.
Perturbation Kernel and Prior Distribution
위 섹션은 스텝간의 kernel에 대해 설명했다면 이제 전체 스텝 즉 $\mathbf{x}_0$과 $\mathbf{x}_i$에 대해 식을 정리하면 다음과 같다.
\[\begin{align} p(\mathbf{x}_i \mid \mathbf{x}_0) &:= \mathcal{N}(\mathbf{x}_i ; \bar{\alpha}_i \mathbf{x}_0, (1-\bar{\alpha}_i^2)\mathbf{I}) \\ \bar{\alpha}_i &:= \Pi_{k=1}^i \sqrt{1-\beta_k^2} = \Pi_{k=1}^i \alpha_k \end{align}\]마찬가지로 위에서 iterative하게 표현한 식도 $\mathbf{x}_0$에 대해서 다음과 같이 쓸 수 있다.
\[\begin{align} \mathbf{x}_i = \bar{\alpha}_i \mathbf{x}_0 + (1-\bar{\alpha}_i^2) \mathbf{\epsilon}_i, \quad \mathbf{\epsilon}_i \sim \mathcal{N}(\mathbf{0}, \mathbf{I}) \end{align}\]결국 마지막 step $L$로 가면 forward process는 $\mathcal{N}(\mathbf{0}, \mathbf{I})$로 수렴한다.
\[\begin{equation} p_L (\mathbf{x}_L \mid \mathbf{x}_0) \longrightarrow \mathcal{N}(\mathbf{0}, \mathbf{I}) \quad \text{as} \quad L \rightarrow \infty \end{equation}\]이 과정을 통해 $p_{\text{data}}$는 점차 $\mathcal{N} (\mathbf{0, I})$가 되고, $\mathbf{x}_0$에 의존하지 않는 prior가 된다.
\[\begin{equation} p_{\text{prior}} := \mathcal{N}(\mathbf{0}, \mathbf{I}) \end{equation}\]Reverse Denoising Process (Learnable Decoder)
Encoder는 고정된 스케줄이니 모델이라고 할 수는 없지만 실제 DDPM의 코어는 모델로 learnable한 Decoder에 있다. 다음 그림과 같이 $x_{L} \sim p_{\text{prior}}$로부터 시작해서 denoise과정을 통해 일관성 있고(coherent) 의미있는(meaningful) 데이터 분포를 도출하는 것이 Decoder의 목적이다.
즉 복잡한 분포 \(\mathbf{x}_i \sim p_i (\mathbf{x})\)를 고려할 때, 정확하게 혹은 최소한 효과적으로 reverse transition kernel \(p(\mathbf{x}_{i-1} \mid \mathbf{x}_{i})\)를 근사할 수 있는가?라는 질문으로 문제를 정의할 수 있다.
Overview: Modeling and Training Objective
위에서 살펴봤듯이, 최종 목적은 unknown true reverse transition kernel \(p(\mathbf{x}_{i-1} \mid \mathbf{x}_{i})\)를 추정하는 것이다. 이를 추정하는 커널을 parameterized reverse transition kernel \(p_\phi (\mathbf{x}_{i-1} \mid \mathbf{x}_{i})\)이라고 하자. 그러면 위 문제를 다음과 같은 KL Divergence를 minimize하는 문제로 바꿀 수 있다.
\[\begin{equation} \text{minimize} \quad \mathbb{E}_{p_i (\mathbf{x}_i)} \left[ \mathcal{D}_{KL} (p (\mathbf{x}_{i-1} \mid \mathbf{x}_{i}) \| p_\phi (\mathbf{x}_{i-1} \mid \mathbf{x}_{i}))\right] \end{equation}\]하지만 \(p (\mathbf{x}_{i-1} \mid \mathbf{x}_{i})\)를 추정하는 것은 쉽지 않다. 어떻게 보면 VAE때랑 비슷한데
\(\begin{equation} p (\mathbf{x}_{i-1} \mid \mathbf{x}_{i}) = p (\mathbf{x}_{i} \mid \mathbf{x}_{i-1}) \underbrace{\dfrac{p_{i-1} (\mathbf{x}_{i-1})}{p_{i} (\mathbf{x}_{i})}}_{\text{intractable}} \end{equation}\) 이기 때문인데, 이는 \(p_{i} (\mathbf{x}_{i})\)를 표현하는 다음 식에서 원본 데이터의 $p_{\text{data}}$의 분포는 샘플링된 데이터로부터 추정할 뿐이지 실제 분포는 일반적으로는 알 수 없기 때문이다.
\[\begin{equation} p_{i} (\mathbf{x}_{i}) = \int p_{i} (\mathbf{x}_{i} \mid \mathbf{x}_0) p_{\text{data}} (\mathbf{x}_0) d \mathbf{x}_0 \end{equation}\]| 비교 항목 | VAE (Variational Autoencoder) | DDPM (Denoising Diffusion) |
|---|---|---|
| 알고 싶은 분포 | true posterior $p(\mathbf{z} \mid \mathbf{x})$ | true reverse kernel $p(\mathbf{x}_{i-1} \mid \mathbf{x}_i) $ |
| 베이즈 정리 | $p(\mathbf{z} \mid \mathbf{x}) = \frac{p(\mathbf{x} \mid \mathbf{z}) p(\mathbf{z})}{p(\mathbf{x})} $ | \(p(\mathbf{x}_{i-1} \mid \mathbf{x}_{i}) = \frac{p(\mathbf{x}_{i} \mid \mathbf{x}_{i-1}) p_{i-1}(\mathbf{x}_{i-1})}{p_{i}(\mathbf{x}_{i})}\) |
| Intractable 항 | \(p(\mathbf{x}) = \int p(\mathbf{x} \mid \mathbf{z}) p(\mathbf{z}) d\mathbf{z}\) | \(p_i(\mathbf{x}_i) = \int p_i(\mathbf{x}_i \mid \mathbf{x}_0) p_{\text{data}}(\mathbf{x}_0) d\mathbf{x}_0\) |
| 해결책 (근사) | 근사 posterior: \(q_\phi(\mathbf{z} \mid \mathbf{x})\) | 근사 reverse kernel: \(p_\phi(\mathbf{x}_{i-1} \mid \mathbf{x}_{i})\) |
Overcoming Intractability with Conditioning
$p_{i} (\mathbf{x}_{i})$를 직접 계산하는건 intractable하다는 것은 알았다. 이제 DDPM의 가장 중요한 직관이 등장한다. 바로 Conditioning을 통해 $p_{i} (\mathbf{x}_{i})$ 대신에 \(p_{i} (\mathbf{x}_{i} \mid \mathbf{x})\)를 사용하는 것이다.
\[\begin{equation} p (\mathbf{x}_{i-1} \mid \mathbf{x}_{i}) = p (\mathbf{x}_{i} \mid \mathbf{x}_{i-1}) \underbrace{\dfrac{p (\mathbf{x}_{i-1} \mid \mathbf{x})}{p (\mathbf{x}_{i} \mid \mathbf{x})}}_{\text{tractable}} \end{equation}\]이것이 가능한 것은 Encoder process가 markov property라 직전 state에만 의존한다는 것이고 \(p (\mathbf{x}_{i} \mid \mathbf{x}_{i-1},\mathbf{x})=p(\mathbf{x}_i \mid \mathbf{x}_{i-1})\), 모든 관련된 distribution이 Gaussian이라 계산이 쉽다는 것이다.
이에 다음과 같은 정리를 도출할 수 있다. $\phi$랑 무관한 상수 $C$가 있다고 하면,
\[\begin{equation*} \begin{aligned} & \mathbb{E}_{p_i (\mathbf{x}_i)} \left[ \mathcal{D}_{KL} (p (\mathbf{x}_{i-1} \mid \mathbf{x}_{i}) \| p_\phi (\mathbf{x}_{i-1} \mid \mathbf{x}_{i}))\right] = \\ & \mathbb{E}_{p_{\text{data}} (\mathbf{x})} \mathbb{E}_{p(\mathbf{x}_i \mid \mathbf{x}) } \left[ \mathcal{D}_{KL} (p (\mathbf{x}_{i-1} \mid \mathbf{x}_{i}, \mathbf{x}) \| p_\phi (\mathbf{x}_{i-1} \mid \mathbf{x}_{i}))\right] + C \end{aligned} \end{equation*}\]이를 증명하려면, 기대값의 정의와 확률의 Chain rule을 사용하고, 로그 함수의 특징을 사용한다. 다만 증명의 편의를 위해 \(\mathbb{E}_{p_{\text{data}} (\mathbf{x})} \mathbb{E}_{p(\mathbf{x}_i \mid \mathbf{x}) } \left[ \mathcal{D}_{KL} (p (\mathbf{x}_{i-1} \mid \mathbf{x}_{i}, \mathbf{x}) \| p_\phi (\mathbf{x}_{i-1} \mid \mathbf{x}_{i}))\right]\)를 분해하는 것부터 증명한다. 어차피 상수는 다른 쪽으로 넘기면 그만이다.
\[\begin{align*} p(\mathbf{x}_0, \mathbf{x_i}) &= p_{\text{data}} (\mathbf{x}_0) p(\mathbf{x}_i \mid \mathbf{x}_0) \end{align*}\]이므로 다음과 같이 $\mathbb{E}$를 하나만 쓰는 식으로 줄일 수 있다.
\[\begin{align*} \mathbb{E}_{p_{\text{data}} (\mathbf{x})} \mathbb{E}_{p(\mathbf{x}_i \mid \mathbf{x}) } \left[ f(\mathbf{x}_0, \mathbf{x}_i) \right] &=\int p_{\text{data}} (\mathbf{x}) \left( \int p(\mathbf{x}_i \mid \mathbf{x}) f(\mathbf{x}_0, \mathbf{x}_i) d\mathbf{x}_i \right) d \mathbf{x}_0 \\ &= \int \int p_{\text{data}} (\mathbf{x}) p(\mathbf{x}_i \mid \mathbf{x}) f(\mathbf{x}_0, \mathbf{x}_i) d\mathbf{x}_i d \mathbf{x}_0 \\ &= \int \int p(\mathbf{x}_0, \mathbf{x_i}) p(\mathbf{x}_i \mid \mathbf{x}) f(\mathbf{x}_0, \mathbf{x}_i) d\mathbf{x}_i d \mathbf{x}_0 \\ &= \mathbb{E}_{\mathbf{x}_0, \mathbf{x_i}} [ f(\mathbf{x}_0, \mathbf{x}_i) ] \end{align*}\]따라서 \(\mathbb{E}_{p_{\text{data}} (\mathbf{x})} \mathbb{E}_{p(\mathbf{x}_i \mid \mathbf{x}) } \left[ \mathcal{D}_{KL} (p (\mathbf{x}_{i-1} \mid \mathbf{x}_{i}, \mathbf{x}) \| p_\phi (\mathbf{x}_{i-1} \mid \mathbf{x}_{i}))\right]\)에 위의 기대값 식을 사용하고, 다시 기대값의 정의를 이용하여 풀어보면 다음과 같다.
\[\begin{equation*} \begin{aligned} & \mathbb{E}_{p (\mathbf{x}_i, \mathbf{x}_0)} \left[ \mathcal{D}_{KL} (p (\mathbf{x}_{i-1} \mid \mathbf{x}_{i}, \mathbf{x}_0) \| p_\phi (\mathbf{x}_{i-1} \mid \mathbf{x}_{i}))\right] = \\ & \int \int p (\mathbf{x}_0, \mathbf{x}_i) \mathcal{D}_{KL} (p (\mathbf{x}_{i-1} \mid \mathbf{x}_{i},\mathbf{x}_{0}) \| p_\phi (\mathbf{x}_{i-1} \mid \mathbf{x}_{i})) d \mathbf{x}_0 d \mathbf{x}_i \end{aligned} \end{equation*}\]로 표현되고, KL Divergence의 정의를 통해 $\mathcal{D}_{KL}$는 다음과 같은 식으로 풀 수 있다.
\[\begin{equation*} \begin{aligned} &\mathcal{D}_{KL} (p (\mathbf{x}_{i-1} \mid \mathbf{x}_{i}) \| p_\phi (\mathbf{x}_{i-1} \mid \mathbf{x}_{i})) = \\ & \int p (\mathbf{x}_{i-1} \mid \mathbf{x}_{i}, \mathbf{x}_0) \log{\dfrac{p (\mathbf{x}_{i-1} \mid \mathbf{x}_{i}, \mathbf{x}_0)}{p_\phi (\mathbf{x}_{i-1} \mid \mathbf{x}_{i})}} d \mathbf{x}_{i-1} \end{aligned} \end{equation*}\]그러면 두 식을 합쳐서 triple integral로 표현할 수 있다. \(\begin{equation*} \begin{aligned} &\mathbb{E}_{p (\mathbf{x}_0, \mathbf{x}_i)} \left[ \mathcal{D}_{KL} (p (\mathbf{x}_{i-1} \mid \mathbf{x}_{i}) \| p_\phi (\mathbf{x}_{i-1} \mid \mathbf{x}_{i}))\right] = \\ & \int \int \int p (\mathbf{x}_0, \mathbf{x}_i) p (\mathbf{x}_{i-1} \mid \mathbf{x}_{i}, \mathbf{x}_0) \log{\dfrac{p (\mathbf{x}_{i-1} \mid \mathbf{x}_{i}, \mathbf{x}_0)}{p_\phi (\mathbf{x}_{i-1} \mid \mathbf{x}_{i})}} d \mathbf{x}_{i-1} d \mathbf{x}_0 d \mathbf{x}_i \end{aligned} \end{equation*}\)
여기에 probability의 chain rule을 적용해보자.
\[\begin{equation*} p(\mathbf{x}_0, \mathbf{x}_i) = p(\mathbf{x}_i) p(\mathbf{x}_0 \mid \mathbf{x}_i) \end{equation*}\]그러면 위 triple integral은 다음과 같이 표현된다.
\[\begin{equation*} \begin{aligned} &\mathbb{E}_{p (\mathbf{x}_0, \mathbf{x}_i)} \left[ \mathcal{D}_{KL} (p (\mathbf{x}_{i-1} \mid \mathbf{x}_{i}) \| p_\phi (\mathbf{x}_{i-1} \mid \mathbf{x}_{i}))\right] \\ &= \int p(\mathbf{x}_i) \int p(\mathbf{x}_0 \mid \mathbf{x}_i) \int p (\mathbf{x}_{i-1} \mid \mathbf{x}_{i}, \mathbf{x}_0) \log{\dfrac{p (\mathbf{x}_{i-1} \mid \mathbf{x}_{i}, \mathbf{x}_0)}{p_\phi (\mathbf{x}_{i-1} \mid \mathbf{x}_{i})}} d \mathbf{x}_{i-1} d \mathbf{x}_0 d \mathbf{x}_i \end{aligned} \end{equation*}\]이는 결국 또다시 기대값의 정의와 부합되므로 세 개의 기대값의 조합으로 표현할 수 있다.
\[\begin{equation*} \begin{aligned} &\mathbb{E}_{p (\mathbf{x}_0, \mathbf{x}_i)} \left[ \mathcal{D}_{KL} (p (\mathbf{x}_{i-1} \mid \mathbf{x}_{i}) \| p_\phi (\mathbf{x}_{i-1} \mid \mathbf{x}_{i}))\right] = \\ & \mathbb{E}_{p(\mathbf{x}_i)} \left[ \mathbb{E}_{p(\mathbf{x}_0 \mid \mathbf{x}_i)} \left[ \mathbb{E}_{p (\mathbf{x}_{i-1} \mid \mathbf{x}_{i}, \mathbf{x}_0)} \left[ \log{\dfrac{p (\mathbf{x}_{i-1} \mid \mathbf{x}_{i}, \mathbf{x}_0)}{p_\phi (\mathbf{x}_{i-1} \mid \mathbf{x}_{i})}} \right] \right] \right] \end{aligned} \end{equation*}\]이제 안쪽 log를 다음과 같이 풀어쓸 수 있다.
\[\begin{equation*} \begin{aligned} \log{\dfrac{p (\mathbf{x}_{i-1} \mid \mathbf{x}_{i}, \mathbf{x}_0)}{p_\phi (\mathbf{x}_{i-1} \mid \mathbf{x}_{i})}} = \log{\dfrac{p (\mathbf{x}_{i-1} \mid \mathbf{x}_{i}, \mathbf{x}_0)}{p (\mathbf{x}_{i-1} \mid \mathbf{x}_{i})}} + \log{\dfrac{p (\mathbf{x}_{i-1} \mid \mathbf{x}_{i})}{p_\phi (\mathbf{x}_{i-1} \mid \mathbf{x}_{i})}} \end{aligned} \end{equation*}\]이 로그식을 위의 기대값식과 결합하면 다음과 같이 전개가 된다. 두번째 term이 전개되는 이유는 $\mathbf{x}_0$과 관련이 없기 때문이다.
\[\begin{align*} \mathbb{E}_{p (\mathbf{x}_0, \mathbf{x}_i)} & \left[ \mathcal{D}_{KL} (p (\mathbf{x}_{i-1} \mid \mathbf{x}_{i}) \| p_\phi (\mathbf{x}_{i-1} \mid \mathbf{x}_{i}))\right] \\ &= \mathbb{E}_{p(\mathbf{x}_i)} \left[ \mathbb{E}_{p(\mathbf{x}_0 \mid \mathbf{x}_i)} \left[ \mathbb{E}_{p (\mathbf{x}_{i-1} \mid \mathbf{x}_{i}, \mathbf{x}_0)} \left[ \log{\dfrac{p (\mathbf{x}_{i-1} \mid \mathbf{x}_{i}, \mathbf{x}_0)}{p (\mathbf{x}_{i-1} \mid \mathbf{x}_{i})}} \right] \right] \right] \\ &+ \mathbb{E}_{p(\mathbf{x}_i)} \left[ \mathbb{E}_{p(\mathbf{x}_0 \mid \mathbf{x}_i)} \left[ \mathbb{E}_{p (\mathbf{x}_{i-1} \mid \mathbf{x}_{i}, \mathbf{x}_0)} \left[ \log{\dfrac{p (\mathbf{x}_{i-1} \mid \mathbf{x}_{i})}{p_\phi (\mathbf{x}_{i-1} \mid \mathbf{x}_{i})}} \right] \right] \right] \\ &= \mathbb{E}_{p(\mathbf{x}_i)} \mathbb{E}_{p(\mathbf{x}_0 \mid \mathbf{x}_i)} \left[ \mathcal{D}_{KL} (p(\mathbf{x}_{i-1} \mid \mathbf{x}_i, \mathbf{x}_0) \| p (\mathbf{x}_{i-1} \mid \mathbf{x}_i)) \right] \\ &+ \mathbb{E}_{p(\mathbf{x}_i)} \left[ \mathbb{E}_{p(\mathbf{x}_0 \mid \mathbf{x}_i)} \left[ \mathbb{E}_{p (\mathbf{x}_{i-1} \mid \mathbf{x}_{i}, \mathbf{x}_0)} \left[ \log{\dfrac{p (\mathbf{x}_{i-1} \mid \mathbf{x}_{i})}{p_\phi (\mathbf{x}_{i-1} \mid \mathbf{x}_{i})}} \right] \right] \right] \\ &= \mathbb{E}_{p(\mathbf{x}_i)} \left[ \mathbb{E}_{p(\mathbf{x}_0 \mid \mathbf{x}_i)} \left[ \mathcal{D}_{KL} (p(\mathbf{x}_{i-1} \mid \mathbf{x}_i, \mathbf{x}_0) \| p (\mathbf{x}_{i-1} \mid \mathbf{x}_i)) \right] \right] \\ &+ \mathbb{E}_{p(\mathbf{x}_i)} \left[ \mathbb{E}_{p (\mathbf{x}_{i-1} \mid \mathbf{x}_{i})} \left[ \log{\dfrac{p (\mathbf{x}_{i-1} \mid \mathbf{x}_{i})}{p_\phi (\mathbf{x}_{i-1} \mid \mathbf{x}_{i})}} \right] \right] \\ &= \mathbb{E}_{p(\mathbf{x}_i)} \left[ \mathbb{E}_{p(\mathbf{x}_0 \mid \mathbf{x}_i)} \left[ \mathcal{D}_{KL} (p(\mathbf{x}_{i-1} \mid \mathbf{x}_i, \mathbf{x}_0) \| p (\mathbf{x}_{i-1} \mid \mathbf{x}_i)) \right] \right] \\ &+ \mathbb{E}_{p(\mathbf{x}_i)} \left[ \mathcal{D}_{KL} (p (\mathbf{x}_{i-1} \mid \mathbf{x}_{i}) \| p_\phi (\mathbf{x}_{i-1} \mid \mathbf{x}_{i})) \right] \end{align*}\]이를 정리하면 다음과 같다.
\[\begin{align*} \mathbb{E}_{p (\mathbf{x}_0, \mathbf{x}_i)} & \left[ \mathcal{D}_{KL} (p (\mathbf{x}_{i-1} \mid \mathbf{x}_{i}) \| p_\phi (\mathbf{x}_{i-1} \mid \mathbf{x}_{i}))\right] \\ &= \mathbb{E}_{p(\mathbf{x}_i)} \left[ \mathbb{E}_{p(\mathbf{x}_0 \mid \mathbf{x}_i)} \left[ \mathcal{D}_{KL} (p(\mathbf{x} _{i-1} \mid \mathbf{x}_i, \mathbf{x}_0) \| p (\mathbf{x}_{i-1} \mid \mathbf{x}_i)) \right] \right] \\ &+ \mathbb{E}_{p(\mathbf{x}_i)} \left[ \mathcal{D}_{KL} (p (\mathbf{x}_{i-1} \mid \mathbf{x}_{i}) \| p_\phi (\mathbf{x}_{i-1} \mid \mathbf{x}_{i})) \right] \\ &= \mathbb{E}_{p(\mathbf{x}_i)} \left[ \mathcal{D}_{KL} (p (\mathbf{x}_{i-1} \mid \mathbf{x}_{i}) \| p_\phi (\mathbf{x}_{i-1} \mid \mathbf{x}_{i})) \right] + C \end{align*}\]여기서 $C$는 모델 파라미터 $\phi$에 의존하지 않는 항이고 단순 noise scheduling에 결정되는 항이므로 상수라는 것이 성립된다.
\[\begin{equation*} C' := \mathbb{E}_{p(\mathbf{x}_i)} \left[ \mathbb{E}_{p(\mathbf{x}_0 \mid \mathbf{x}_i)} \left[ \mathcal{D}_{KL} (p(\mathbf{x}_{i-1} \mid \mathbf{x}_i, \mathbf{x}_0) \| p (\mathbf{x}_{i-1} \mid \mathbf{x}_i)) \right] \right] \end{equation*}\]이걸 $C’$를 역으로 넘기면 Equivalence Between Marginal and Conditional KL Minimization라는 Theorem을 정의할 수 있다. $-$는 상수니까 상관없으므로 $C = -C’$라고 하면 맨 처음 증명하고자 했던 그 식이 나온다.
\[\begin{align*} \mathbb{E}_{p(\mathbf{x}_i)} &\left[ \mathcal{D}_{KL} (p (\mathbf{x}_{i-1} \mid \mathbf{x}_{i}) \| p_\phi (\mathbf{x}_{i-1} \mid \mathbf{x}_{i})) \right] \\ &= \mathbb{E}_{p (\mathbf{x}_0, \mathbf{x}_i)} \left[ \mathcal{D}_{KL} (p (\mathbf{x}_{i-1} \mid \mathbf{x}_{i}) \| p_\phi (\mathbf{x}_{i-1} \mid \mathbf{x}_{i}))\right] + C \\ &= \mathbb{E}_{p_{\text{data}} (\mathbf{x})} \mathbb{E}_{p (\mathbf{x}_i \mid \mathbf{x})} \left[ \mathcal{D}_{KL} (p (\mathbf{x}_{i-1} \mid \mathbf{x}_{i}) \| p_\phi (\mathbf{x}_{i-1} \mid \mathbf{x}_{i}))\right] + C \end{align*}\]이 식은 DDPM을 관통하는 중요한 원리이다. 현재 포스트와 같은 Variational한 접근뿐만 다른 접근에서도 통찰하는 원리인 것이다.
marginal distribution의 KL divergence를 minimize하는 것은 실제로는 특정 condiitional distribution을 minimize하는 것과 같다.
이것을 바탕으로 다음과 같은 Reverse Conditional Transition Kerne에 대한 Lemma를 도출할 수 있다.
\(p(\mathbf{x}_{i-1} \mid \mathbf{x}_i, \mathbf{x})\)는 다음과 같이 closed Gaussian form으로 표현된다.
\[\begin{align} p(\mathbf{x}_{i-1} \mid \mathbf{x}_i, \mathbf{x}) = \mathcal{N} (\mathbf{x}_{i-1};\mathbf{\mu}(\mathbf{x}_i, \mathbf{x}, i ), \sigma^2 (i) \mathbf{I}) \end{align}\]이 때 각 $\mathbf{\mu}$와 $\sigma^2 (i)$ 는 노이즈 스케줄링을 담당하는 $\beta_i$에 의해 다음과 같이 정의된다. $\alpha_i$와 $\bar{\alpha}_i$도 참고를 위해 다시 작성했다.
\[\begin{align} \mathbf{\mu}(\mathbf{x}_i, \mathbf{x}, i ) &:= \dfrac{\bar{\alpha}_{i-1} \beta^2_i}{1-\bar{\alpha}_{i}^2 } \mathbf{x}+ \dfrac{(1-\bar{\alpha}^2_{i-1}) \alpha_i}{1-\bar{\alpha}^2_{i}} \mathbf{x}_i \\ \sigma^2 (i) &:= \dfrac{1-\bar{\alpha}_{i-1}}{1-\bar{\alpha}_{i} } \beta^2_i \\ \alpha_i &= \sqrt{1-\beta^2} \\ \bar{\alpha}_i &= \Pi_{k=1}^i \sqrt{1-\beta_k^2} = \Pi_{k=1}^i \alpha_k \end{align}\]Modeling of Reverse Transition Kernel
결국 남은 문제는 Reverse Transition Kernel \(p_\phi (\mathbf{x}_{i-1} \mid \mathbf{x}_i)\)를 어떻게 모델링할 것인가가 남는다. 이전 섹션 Theorem과 Lemma을 결합하면 각 reverse transition kernel은 다음과 같이 정의될 수 있다.
\[\begin{align} p_\phi (\mathbf{x}_{i-1} \mid \mathbf{x}_i) := \mathcal{N}(\mathbf{x}_{i-1};\mathbf{\mu}_\phi (\mathbf{x}_i, i), \sigma^2(i)\mathbf{I}) \end{align}\]이 때 $\mathbf{\mu}_\phi (\cdot, i): \mathbb{R}^D \rightarrow \mathbb{R}^D$는 learnable한 mean function이고, $\sigma^2(i) \geq 0$은 Lemma에 정의된 것처럼 positive한 양수이다.
결국 loss function은 모든 step에 대해 평균을 낸 KL Divergence이다.
\[\begin{align} \mathcal{L}_{\text{diffusion}} (\mathbf{x}_0 ; \phi) := \sum_{i=1}^L \mathbb{E}_{p(\mathbf{x}_i \mid \mathbf{x}_0)} \left[ \mathcal{D}_{KL} (p(\mathbf{x}_{i-1} \mid \mathbf{x}_i, \mathbf{x}_0) \| p_\phi (\mathbf{x}_{i-1} \mid \mathbf{x}_i)) \right] \end{align}\]그러면 Gaussian 의 정의와 위에서 parameterized된 $\mu$의 힘을 빌리면
\[\begin{align*} \mathcal{L}_{\text{diffusion}} (\mathbf{x}_0 ; \phi) = \sum_{i=1}^L \dfrac{1}{\sqrt{2\sigma^2 (i)}} \| \mathbf{\mu}_\phi (\mathbf{x}_i, i) - \mathbf{\mu} (\mathbf{x}_i, \mathbf{x}_0, i) \|^2_2 + C \end{align*}\]$C$는 minimize 할 때는 필요가 없는 상수이고, 위 식을 전체 data distribution \(\mathbf{x}_0 \sim p_{\text{data}}\)에 대해 평균을 내면 다음과 같은 DDPM의 최종 loss function이 도출된다.
\[\begin{align} \mathcal{L}_{\text{DDPM}} (\phi) := \sum_{i=1}^L \dfrac{1}{\sqrt{2\sigma^2 (i)}} \mathbb{E}_{\mathbf{x}_0} \mathbb{E}_{p(\mathbf{x}_i \mid \mathbf{x}_0)} \left[ \| \mathbf{\mu}_\phi (\mathbf{x}_i, i) - \mathbf{\mu} (\mathbf{x}_i, \mathbf{x}_0, i) \|^2_2 \right] \end{align}\]Practical Choices of Predictions and Loss
하지만 실제로는 위 loss를 직접 사용하는 일은 없다. 왜냐하면, \(\| \mathbf{\mu}_\phi (\mathbf{x}_i, i) - \mathbf{\mu} (\mathbf{x}_i, \mathbf{x}_0, i) \|^2_2\) 이 값이 복잡한 $\mathbf{\mu}$는 복잡하여 예측하기도 어렵고, 타임스텝에 따라 $\mu$의 중요도가 변하며 (노이즈가 적은 초반에는 $\mu$에 민감, 후반에는 noise에 의해 $\mu$가 묻힘), 앞으로 증명하겠지만 $\epsilon$이 $\mu$와 동등(reparameterization trick)하기 때문이다.
$\epsilon$-prediction
DDPM forward process를 다시 떠올려 보면 noise level $i$에서 생성되는 noisy sample \(x_i \sim p(\mathbf{x}_i \mid \mathbf{x})\)는 다음과 같은 식에 의해서 생성된다.
\[\begin{equation} \mathbf{x}_i = \bar{\alpha}_i \mathbf{x}_0 + \sqrt{1- \bar{\alpha}_i^2} \epsilon, \quad \mathbf{x}_0 \sim p_{\text{data}}, \quad \epsilon \sim \mathcal{N}(\mathbf{0, I}) \end{equation}\]이걸로 \(\mathbf{\mu}(\mathbf{x}_i, \mathbf{x}, i )\)를 \(\mathbf{\mu}(\mathbf{x}_i, \mathbf{x}_0, i )\)로 바꾼 다음 다시 전개해보자. 이 때 목표로 하는 것은 $\mathbf{x}_0$을 $\mathbf{x}_i, \mathbf{\epsilon}$으로 치환하는 것이다. 따라서 \(\mathbf{x}_i\) 식을 \(\mathbf{x}_0\)에 대해서 다시 정리한다.
\[\begin{align*} \mathbf{x}_0 = \dfrac{1}{\bar{\alpha}_i} \left( \mathbf{x}_i - \sqrt{1 - \bar{\alpha}_i^2} \mathbf{\epsilon}\right) \end{align*}\]이 때, \(\bar{\alpha}_i = \alpha_i \bar{\alpha}_{i-1}\) 과 \(\beta_i^2 = 1 - \alpha_i^2\)를 조합하면
\[\begin{align*} \mathbf{\mu}(\mathbf{x}_i, \mathbf{x}_0, i ) &= \dfrac{\bar{\alpha}_{i-1} \beta^2_i}{1-\bar{\alpha}_{i}^2 } \mathbf{x}_0 + \dfrac{(1-\bar{\alpha}^2_{i-1}) \alpha_i}{1-\bar{\alpha}^2_{i}} \mathbf{x}_i \\ \mathbf{\mu}(\mathbf{x}_i, \mathbf{\epsilon}, i ) &= \dfrac{\bar{\alpha}_{i-1} \beta^2_i}{1-\bar{\alpha}_{i}^2 } \dfrac{1}{\bar{\alpha}_i} \left( \mathbf{x}_i - \sqrt{1 - \bar{\alpha}_i^2} \mathbf{\epsilon}\right) +\dfrac{(1-\bar{\alpha}^2_{i-1}) \alpha_i}{1-\bar{\alpha}^2_{i}} \mathbf{x}_i \\ &= \dfrac{A}{\bar{\alpha}_i} (\mathbf{x}_i - \sqrt{1 - \bar{\alpha}_i^2} \mathbf{\epsilon}) + B \mathbf{x}_i \\ &= \left(\dfrac{A}{\bar{\alpha}_i} + B\right) \mathbf{x}_i - \dfrac{A}{\bar{\alpha}_i} \sqrt{1 - \bar{\alpha}_i^2} \mathbf{\epsilon} \\ &= \dfrac{1}{\alpha_i} \mathbf{x}_i - \dfrac{1 - \alpha_i^2}{\alpha_i \sqrt{1 - \bar{\alpha}_i^2}} \mathbf{\epsilon} \\ &= \dfrac{1}{\alpha_i} \left(\mathbf{x}_i - \dfrac{1 - \alpha_i^2}{\sqrt{1 - \bar{\alpha}_i^2}} \mathbf{\epsilon} \right) \end{align*}\]모델을 이용하여 \(\mathbf{\mu}_\phi\)를 \(\mathbf{\epsilon}_\phi (\mathbf{x}_i, i)\)로 parameterize하면 다음과 같다.
\[\begin{align} \mathbf{\mu}_\phi(\mathbf{x}_i, i ) = \dfrac{1}{\alpha_i} \left(\mathbf{x}_i - \dfrac{1 - \alpha_i^2}{\sqrt{1 - \bar{\alpha}_i^2}} \underbrace{\mathbf{\epsilon}_\phi (\mathbf{x}_i, i)}_{\epsilon\text{-prediction}} \right) \end{align}\]이를 원래 Loss인 \(\mathcal{L}_{\text{DDPM}} (\phi)\)에 넣으면 다음과 같이 reparameterization이 일어난다.
\[\begin{align} \| \mathbf{\mu}_\phi (\mathbf{x}_i, i) - \mathbf{\mu} (\mathbf{x}_i, \mathbf{x}_0, i) \|^2_2 &\propto \| \mathbf{\epsilon}_\phi (\mathbf{x}_i, i) - \mathbf{\epsilon} \|^2_2 \\ \| \mathbf{\mu}_\phi (\mathbf{x}_i, i) - \mathbf{\mu} (\mathbf{x}_i, \mathbf{x}_0, i) \|^2_2 &= C_i \| \mathbf{\epsilon}_\phi (\mathbf{x}_i, i) - \mathbf{\epsilon} \|^2_2 \\ \end{align}\]참고로 \(\propto\)를 \(=\)로 바꾸는 과정에서 $i$에 의존하는 weight $C_i$가 들어간다.
$\epsilon$-prediction is a noise detective
이렇게 DDPM은 노이즈 탐지기(noise detective)의 역할을 수행한다. 복잡한 $\mathbf{\mu}_i$대신에 $\mathbf{\epsilon}_i$을 예측하면서 특정 스텝 $i$에 들어가는 노이즈의 분포를 예측하는 것이다.
- noisy한 이미지를 보고
- “이 이미지에 어떤 노이즈가 섞여있나?”를 분석하여
- 그 노이즈를 정확히 복원 (모델의 output)
- 그걸 빼서 $x_0$에 가까운 값을 얻음
과 같은 작용을 한다. 모델의 출력은 noise고 해당 step에서 noise만 뺀 뒤 $\mu$를 계산하고 posterior mean \(\mathbf{\mu}(\mathbf{x}_i, \mathbf{\epsilon}_i , i)\)을 계산한 다음 \(x_{i-1}\)을 샘플링 하는 것이다.
이 때 모델은 UNet이나 Transformer같은 백본 모델을 써서 입력 이미지의 noisy한 feature를 분석해 noise component(\(\epsilon\))를 예측하는 map으로 반환한다.
Simplified Loss with $\epsilon$-prediction
$\epsilon$-prediction에서 \(\mathbf{\mu}\)와의 연결을 위해 $C_i$라는 $i$에 dependent한 weight를 도입했는데, 실제로는 이 weight가 없어도 된다는 것이 밝혀졌다.
\[\begin{align} \mathcal{L}_{\text{simple}}(\phi) := \mathbb{E}_{i}\, \mathbb{E}_{\mathbf{x} \sim p_{\text{data}}(\mathbf{x})}\, \mathbb{E}_{\epsilon \sim \mathcal{N}(0, \mathbf{I})} \left[ \left\| \epsilon_{\phi}(\mathbf{x}_i, i) - \epsilon \right\|_2^2 \right] \end{align}\]왜냐하면 \(\mathcal{L}_{\text{simple}}(\phi)\)나 \(\mathcal{L}_{\text{DDPM}}(\phi)\)이나 결국 동일한 문제를 푸는 least square problem이기 때문에 동일한 optimal solution \(\epsilon^* (x_i, i)\)를 가지기 때문이다.
$\epsilon$-prediction 모델은 $\mathbf{x}_i$가 주어졌을 때, forward diffusion 과정에서 실제로 들어간 노이즈 $\mathbf{\epsilon}$의 조건부 기대값을 출력한다.
\[\begin{equation} \epsilon^* (x_i, i) = \mathbb{E} [\mathbf{\epsilon} \mid \mathbf{x}_i ] \end{equation}\]\(\mathbf{x}_i\)는
\[\begin{equation} \mathbf{x}_i = \bar{\alpha}_i \mathbf{x}_0 + \sqrt{1-\bar{\alpha}^2_i } \mathbf{\epsilon} \end{equation}\]이렇게 $\mathbf{x}_0$와 $\epsilon$이 섞여서 구성되어 있다.
우리의 입력은 $\mathbf{x}_i$이고, $\mathbf{\epsilon}$은 target이지만 훈련할때는 알고있다. 일종의 $\hat{y}$같은 것이기 때문이다.
즉 기존 딥러닝 모델과 마찬가지로 다음 문제를 푸는 것이 주 목적이다. \(\min_\phi \mathbb{E} \| \hat{y}(\phi) - y \|^2\)와 다를 바가 없는 식이다.
\[\begin{equation} \min_\phi \mathbb{E} \| \mathbf{\epsilon}_\phi (\mathbf{x}_i, i) - \mathbf{\epsilon} \|^2 \end{equation}\]L2 regression의 기본 성질에 따라, 모델은 $\mathbf{\epsilon}$자체를 학습하는 것이 아니라 $\mathbf{x}_i$를 보고 가능한 $\mathbf{\epsilon}$들의 평균(조건부 기대값)을 추정한다.
알고보니까 \(\| \mathbf{\mu}_\phi (\mathbf{x}_i, i) - \mathbf{\mu} \|^2\) 이거나 \(w_i \| \mathbf{\epsilon}_\phi (\mathbf{x}_i, i) - \mathbf{\epsilon} \|^2\)이거나 \(\| \mathbf{\epsilon}_\phi (\mathbf{x}_i, i) - \mathbf{\epsilon} \|^2\) 결국 \(\epsilon^* (x_i, i)\)를 찾는 문제라는 것이 증명되었고, 그러면 제일 간단한 \(\| \mathbf{\epsilon}_\phi (\mathbf{x}_i, i) - \mathbf{\epsilon} \|^2\)를 쓰는 것이 당연한 것이다.
Conclusion
책에는 $x$-prediction이나 Sampling에 관한 더 재밌는 얘기가 많지만 이정도로 충분한 것같다. 결국 VAE는 $z$로부터 한번에 $x$를 생성하려고 했으나, $x$가 multi-peak분포라면 모두를 포함하기 위해 더 넓은 Gaussian이 되어야 하고, average효과가 나오게 된다. 이로 인해 blurry한 이미지 생성이 발생한다.
그러나, DDPM은 이걸 refine하는 과정을 추가하여 high to low방식으로 noise를 추가하여 초반에는 global한 structure를 후반에는 detail을 추가하는 방식으로 해결하였다. 그러나 이 과정은 iterative하기 때문에 필연적으로 느린 생성 속도를 유발하게 된다. 요즘은 이 생성속도를 해결하기 위한 수치해석적 방법을 결합한 생성방법이 존재하며, 다른 챕터에서 그것을 다루고 있다.
Reference
- [1]C.-H. Lai, Y. Song, D. Kim, Y. Mitsufuji, and S. Ermon, “The Principles of Diffusion Models,” arXiv preprint arXiv:2510.21890, 2025.
- [2]S. Dieleman, “Diffusion models are autoencoders.” 2022. Available at: https://benanne.github.io/2022/01/31/diffusion.html