Singular Value Decomposition

Introduction

SVD(Singular Value Decomposition)는 LLM을 공부하다보면 참 이곳저곳에서 많이 나오는 알고리즘이다. 특히 (Strang and others 2019)에서도 Data Science meets linear algebra in the SVD라고 시작하고, Low Level Technicals of LLMs: Daniel Han에서도 그 중요성을 강조하고 있다.

그래서 오늘은 SVD에 대해 좀 더 집중적으로 탐구해보고자 한다.

\[\mathbf{M} = \mathbf{U} \mathbf{\Sigma} \mathbf{V}^\top\]

Basic problems of Linear Algebra

(Strang and others 2019)에서는 가장 기본적인 선형대수(Linear Algebra)의 문제로 다음 5가지를 꼽고 있다.

• $\mathbf{A}\mathbf{x}=\mathbf{b}$
• $\mathbf{A}\mathbf{x}=\lambda \mathbf{x}$
• $\mathbf{A}\mathbf{v}= \sigma \mathbf{u}$
• Minimize $\lVert \mathbf{A}\mathbf{x} \rVert^2 / \lVert \mathbf{x} \rVert^2$
• Factor the matrix $\mathbf{A}$

그리고 각각에 대해 중요한 질문과 답을 던진다. 이 글에서는 $\mathbf{A}\mathbf{x}=\mathbf{b}$ $\mathbf{A}\mathbf{v}= \sigma \mathbf{u}$를 중점적으로 볼 예정이다.

• $\mathbf{A}\mathbf{x}=\mathbf{b}$
  • Solution $\mathbf{x}$는 존재하는가? 즉, vector $\mathbf{b}$는 $\mathbf{A}$의 column space에 속한다고 할 수 있는가?
• $\mathbf{A}\mathbf{x}=\lambda \mathbf{x}$
  • $\mathbf{A}\mathbf{x}$는 $\mathbf{x}$와 같은 방향을 유지하는가? 즉, 복잡한 $\mathbf{A}$를 $\lambda$로 단순화 시킬 수 있다.
• $\mathbf{A}\mathbf{v}= \sigma \mathbf{u}$
  • 벡터 2개 $\mathbf{u}$와 $\mathbf{v}$가 존재하고, $\mathbf{A}$는 rectangular하며 data로 가득찼을 때, 과연 어떤 data matrix가 중요한가? 여기서 해답은 SVD인 $\sigma \mathbf{u} \mathbf{v}^\mathsf{T}$이다. (PCA: Principle Component Analysis)
• Minimization and Fatorization
  • 근본적인 응용수학인 문제로 귀결되며, SVD의 $\mathbf{u}$와 $\mathbf{v}$를 찾는 문제로 귀결된다. 즉, Data를 가장 잘 설명하는 선형대수는 무엇인가?

Matrix-vector multiplication $\mathbf{Ax}$

궁극적인 목표인 SVD를 가기 위해서 matrix multiplication ($\mathbf{AB}$)을 알아야하고, 그걸 위해서는 matrix-vector multiplication ($\mathbf{Ax}$)을 먼저 알아야한다.

Linear combination of vectors

다음과 같은 샘플 $\mathbf{A}$를 다음과 같이 $a_1$과 $a_2$의 조합이라고 생각해보면, 다음과 같이 inner product of rows와 combinations of the columns 2가지 방식으로 생각할 수 있다.

\[\begin{align*} A &= \begin{bmatrix} 2 & 3 \\ 2 & 4 \\ 3 & 7 \end{bmatrix} = \bigl[\, \mathbf{a}_1 \ \mathbf{a}_2 \,\bigr] \\ x &= \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} \\ Ax &= \begin{bmatrix} 2 & 3 \\ 2 & 4 \\ 3 & 7 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} 2 x_1 + 3 x_2 \\ 2 x_1 + 4 x_2 \\ 3 x_1 + 7 x_2 \end{bmatrix} \\ Ax &= x_1 \begin{bmatrix} 2 \\ 2 \\ 3 \end{bmatrix} + x_2 \begin{bmatrix} 3 \\ 4 \\ 7 \end{bmatrix} = \begin{bmatrix} 2 x_1 + 3 x_2 \\ 2 x_1 + 4 x_2 \\ 3 x_1 + 7 x_2 \end{bmatrix} = x_1 a_1 + x_2 a_2 \end{align*}\]

즉, $\mathbf{Ax}$는 $\mathbf{A}$의 columns의 linear combination이며, $\mathbf{A}$의 column들을 Column Space라고 한다.

선형대수를 처음 배우면 이 Space란 말이 추상적이라 어려운데, 방향의 조합으로 만들어지는 공간이라고 생각하면 된다. 일반적으로 쉽게 접하는 2차원 평면은 cartesian coordinate인 $x$축 즉 $(1, 0)$과 $y$축 즉 $(0, 1)$이라는 두 방향의 조합으로 결정되는 공간인 것이다.

즉, 다음과 같이 정의할 수 있다.

Matrix $\mathbf{A}$의 column vector들의 선형 결합(linear combination)은 $\mathbf{A}$의 열공간(Column space)을 이룬다.

Independence and Rank of $\mathbf{A}$

위에서 언급한 $x$축과 $y$축을 생각해보자. 벡터 $(1,0)$과 $(0,1)$을 잡으면 이 두 벡터를 조합해 2차원 공간 $\mathbb{R}^2$의 모든 점을 표현할 수 있다.

그런데 벡터를 다르게 잡으면 문제가 생길 수 있다. 예를 들어 $(1,0)$과 $(3,0)$을 고르면 어떨까? $(3,0)$은 사실 $(1,0)$을 세 배 한 것이므로, 이 둘을 조합해도 결국 $x$축 위의 점들만 얻을 수 있다. 즉, $y$축 방향은 전혀 표현하지 못한다.

이처럼 어떤 벡터들이 서로 “겹치는” 정보를 담고 있으면, 그 벡터들로는 더 넓은 공간을 만들어내지 못한다. 이런 상황을 일반적으로 선형 종속(linear dependence)이라고 부르고, 반대로 벡터들이 서로 겹치지 않고 독립적으로 공간을 구성할 수 있을 때 선형 독립(linear independence)이라고 한다.

이런 차이를 일반적으로 설명하기 위해, 먼저 span이라는 개념을 정의한다.

정의 (Span). 벡터 집합 $ S = \lbrace v_1, v_2, \dots, v_k \rbrace $가 주어졌을 때,

\[\begin{equation} \textrm{Span}(S) = \lbrace a_1 v_1 + a_2 v_2 + \cdots a_k v_k \mid a_1, a_2, \cdots, a_k \in \mathbb{R} \rbrace \end{equation}\]

라고 하며 이는 $S$에 속한 벡터들의 모든 선형 결합으로 얻을 수 있는 벡터들의 집합을 뜻한다.

이제 이 개념을 통해, $(1,0)$과 $(0,1)$은 $\mathbb{R}^2$ 전체를 span하지만, $(1,0)$과 $(3,0)$은 $x$축만 span한다는 사실을 보다 정확히 표현할 수 있다.

여기서 다시 선형 독립의 개념을 떠올려보면, 벡터들이 서로 중복된 정보를 담지 않아야 원하는 공간 전체를 span할 수 있다는 점이 드러난다.

따라서 어떤 벡터 공간을 생각했을 때, 그 공간의 모든 벡터를 표현할 수 있어야 한다는 조건(즉, span이 공간 전체여야 한다)과, 그 벡터들이 서로 겹치지 않는 조건(즉, 선형 독립이어야 한다)을 동시에 만족하는 벡터 집합을 기저(basis)라고 하며 다음과 같이 정의할 수 있다.

어떤 벡터 공간에서,

1. 그 공간 전체를 span하고,
2. 벡터들이 선형 독립일 때

그 벡터 집합을 basis라고 한다.

예를 들어 $\mathbb{R}^2$에서는 $(1,0)$과 $(0,1)$이 대표적인 basis이다. 두 벡터는 서로 독립적이고, 두 벡터의 조합으로 평면 위의 모든 벡터를 만들 수 있기 때문이다. 반대로 $(1,0)$과 $(3,0)$은 $x$축만 span하므로 $\mathbb{R}^2$의 basis가 될 수 없다.

따라서 basis는 공간 전체를 표현할 수 있는 최소한의 벡터 집합이라고 할 수 있다.

Span과 basis가 처음에 헷갈릴 수 있는데, Span은 주어진 벡터들로 만들 수 있는 전체 공간이고, basis는 그 공간을 대표하는 선형 독립적인 벡터이다. basis 자체는 여러개 존재할 수 있으나, basis의 개수는 항상 같고 이를 차원(dimension)으로 일정하다.

이제 어떤 행렬 $\mathbf{A}$의 column space를 생각해 보자. 그 공간의 차원, 즉 기저 벡터의 개수를 rank라고 한다. 다시 말해 rank는 column space의 차원과 같으며, 행렬의 독립적인 열(column)의 개수를 세는 것과 같다. 예를 들어, $\mathbb{R}^2$에서 $(1,0),(0,1) $은 서로 독립이므로 rank는 2가 되고, (1,0),(3,0)처럼 종속된 벡터들만 있다면 rank는 1이 된다. 따라서 rank는 기저 선택과 관계없이 항상 유일하게 정해진다.

마지막으로, 차원(dimension)은 일반적인 벡터 공간의 크기를 말하는 개념이고, rank는 특별히 “행렬이 만드는 column space(또는 row space)의 차원”을 의미한다. 즉, rank는 “행렬에 의해 결정되는 특정한 공간의 차원”이라고 볼 수 있다. 행렬이 없는 차원은 여러가지 의미가 있을 수 있지만, 우리가 보통 아는 그 차원을 생각하면 된다. 직선 $\mathbb{R}^1$은 1차원, 평면 $\mathbb{R}^2$은 2차원, 3차원 공간 $\mathbb{R}^3$은 3차원인 것이다. 그리고 rank는 이러한 일반적인 차원 개념 속에서 “특정 행렬이 실제로 만들어낼 수 있는 방향(독립적인 열/행 벡터)의 수”를 말한다. 따라서 rank는 차원의 특수한 경우라고 이해할 수 있다.

Matrix-matrix multiplication $\mathbf{AB}$

행렬의 곱셈을 설명하는데는 두 가지 관점이 있다. 한 가지는 Inner product 관점이며, 이는 행렬 원소 하나인 scalar를 계산하는데 초점을 둔다. 또 한 가지는 Outer product관점인데, 이는 행렬을 원소가 아니라 여러 rank one matrix의 합으로 본다.

보통 inner product 관점으로 많이 설명한다. 계산절차를 설명하기도 쉽고, 행렬곱셈을 두 행렬의 기하학적인 정렬이라고 이해하기도 쉽다. 하지만 outer product관점이 머신러닝 관점에서 더 유용하다. 왜냐하면 행렬을 여러 기본 성분(rank one matrix)으로 쪼개서 보는 관점이다. 특히 이번 글에서 설명하는 SVD는 이 중에서 중요한 성분만 추출하는 것이기 때문에 outer product관점으로 접근하는것이 훨씬 이해하기가 쉽다.

Inner product perspective (Row × Column)

일반적으로 matrix끼리의 곱셈은 내적(inner product)로 설명을 한다.

$\mathbf{AB}$에서 $\mathbf{A}$의 row와 $\mathbf{B}$의 column을 곱한다는 관점이다.

$\mathbf{A}$의 2번쨰 row와 $\mathbf{B}$의 3번쨰 column vector의 내적이 $\mathbf{C}=\mathbf{AB}$의 원소 $c_{23}$이 되는 것이다.

\[\begin{bmatrix} \cdot & \cdot & \cdot \\ a_{21} & a_{22} & a_{23} \\ \cdot & \cdot & \cdot \end{bmatrix} \begin{bmatrix} \cdot & \cdot & b_{13} \\ \cdot & \cdot & b_{23} \\ \cdot & \cdot & b_{33} \end{bmatrix} = \begin{bmatrix} \cdot & \cdot & \cdot \\ \cdot & \cdot & c_{23} \\ \cdot & \cdot & \cdot \end{bmatrix}\]

이고,

\[\begin{equation*} c_{23} = a_{21} b_{13} + a_{22} b_{23} + a_{23} b_{33} = \sum_{k=1}^{3} a_{2k} b_{k3} \end{equation*}\]

즉 \(\begin{equation} c_{ij} = \sum_{k=1}^{n} a_{ik} b_{kj} \end{equation}\)

Outer product perspective (Column × Row)

하지만 행렬 곱셈 $\mathbf{AB}$를 포현하는 다른 방식으로는 Outer product의 합으로 설명할 수 있는 방법이 있다. 이는 $\mathbf{A}$의 열(column)과 $\mathbf{B}$의 행(row)을 곱하는 관점이다.

\[\begin{equation} AB = \begin{bmatrix} \,|\, & & \,|\, \\ a_{1} & \cdots & a_{n} \\ \,|\, & & \,|\, \end{bmatrix} \begin{bmatrix} - b_1^{*} - \\ \vdots \\ - b_n^{*} - \end{bmatrix} = a_{1} b_{1}^{*} + a_{2} b_{2}^{*} + \cdots + a_{n} b_{n}^{*} \end{equation}\]

이 때, 개별적인 column $\times$ row 방식은 vector가 아니라 rank-one matrix를 만들고 rank-one matrix의 합이 $\mathbf{AB}$를 구성한다.

$\mathbf{A}$의 column vector 하나를 $u$, $\mathbf{B}$의 row vector 하나를 $v^\mathsf{T}$라고 할 때, 모든 열(column)은 $u$의 배수이고, 모든 행(row)는 $v^\mathsf{T}$의 배수이다.

\[\begin{equation} uv^{\mathsf{T}} = \begin{bmatrix} 2 \\ 2 \\ 1 \end{bmatrix} \begin{bmatrix} 3 & 4 & 6 \end{bmatrix} = \begin{bmatrix} 6 & 8 & 12 \\ 6 & 8 & 12 \\ 3 & 4 & 6 \end{bmatrix} \end{equation}\] \[uv^{\mathsf{T}} = \begin{bmatrix} 6 & 8 & 12 \\ 6 & 8 & 12 \\ 3 & 4 & 6 \end{bmatrix}\]

이것이 rank-one matrix의 특징이고, 이 rank-one matrix는 행렬의 기저 역할을 한다. 모든 nonzero 벡터의 외적 $uv^{\mathsf{T}}$는 rank one이며 모든 행렬의 building block라고 할 수 있다.

이걸 확장하면 행렬 곱셈은 여러 개의 외적 = rank one matrix = building block들의 합이라고 볼 수 있다.

Geometric interpretation of outer product perspective

• Rank-one rank과 기본 공간 (Rank-one 행렬의 row space = $v$ 방향 (line through v))
  • 하나의 rank-one matrix $\mathbf{u}\mathbf{v}^{\mathsf{T}}$은 한 쌍의 기본 공간을 정의한다.
  • Row Space: 이 행렬의 Row Space는 입력 방향을 결정하는 벡터 v가 만드는 1차원 공간(선)이다.
  • Column Space: 이 행렬의 Column Space는 출력 방향을 결정하는 벡터 u가 만드는 1차원 공간(선)이다..
  • 즉, 이 행렬은 입력을 v 방향으로 ‘측정’하여, 그 결과를 u 방향으로 ‘사상(mapping)’시키는 가장 단순한 변환기이다.
• 여러 rank-one의 조합 → row space의 span이 확장
  • 모든 행렬 A는 이러한 Rank-one 행렬(벽돌)들의 합으로 표현될 수 있다. $\mathbf{A} = \Sigma \sigma_i u_i v^{\mathsf{T}}_i$가 된다.
  • 즉, 각 rank-one 행렬 $u_i v^{\mathsf{T}}_i$는 특정 입력방향 $v_i$에 반응하여 특정 출력방향 $u_i$로 결과를 내보낸다.
  • Row Space
    • 행렬 $\mathbf{A}$의 row space는 입력방향 벡터 $v_i$가 모여서 만드는 공간(span)이다.
    • 이 공간은 행렬 $\mathbf{A}$가 의미 있게 반응할 수 있는 모든 입력 벡터의 집합이다.
    • 만약 어떤 벡터가 이 Row space에 포함되어 있지 않다면(직교한다면), 행렬 A는 그 벡터를 영벡터($\mathbf{0}$)로 변환한다.
  • Column Space
    • 행렬 $\mathbf{A}$의 column space는 출력방향 벡터 $u_i$가 모여서 만드는 공간(span)이다.
    • 이 공간은 행렬 $\mathbf{A}$가 만들어낼 수 있는 모든 가능한 결과 벡터의 집합이다.
    • 어떤 입력 벡터 $\mathbf{x}$를 사용하든, 그 결과인 $A\mathbf{x}$는 반드시 이 column space 안에 존재하게 된다.

From Matrix Factorization to SVD

머신러닝에서 중요한것은 어떤 것을 feature 혹은 signal로 볼 것인가이다. 노이즈를 제거하고 핵심 정보를 추출하기 위해 행렬(matrix)을 다양한 방식으로 분해(factorization)할 수 있다.

어떤 matrix $\mathbf{A}$를 $\mathbf{CR}$로 분해한다고 가정하자. 이 때 $\mathbf{C}$와 $\mathbf{R}$을 구성하는 방식은 다양하며, LU, QR, 고유분해(diagonalization) 등의 기법이 있고, 이 모든 것을 일반화한 가장 강력한 방식이 바로 SVD이다.

1. LU Decomposition (Elimination)
   • $\mathbf{A} = \mathbf{LU}$
   • $\mathbf{A}$를 Gauss elimination으로 행(row)을 조합해 upper triangular matrix $\mathbf{U}$를 만들고, 소거 과정에서의 계수(coefficient)들을 모아서 lower triangular matrix $\mathbf{L}$를 생성한다.
2. QR Decomposition (Orthogonalization)
   • $\mathbf{A} = \mathbf{QR}$
   • Gram-Schmidt변환을 통해 열(column)을 직교화(Orthogonalizing)한다.
   • $\mathbf{Q}$는 orthonormal columns ( $Q^{\mathsf{T}}Q=I$ ), $\mathbf{R}$은 upper triangular matrix이다.
3. Diagonalization
   • $\mathbf{A} = \mathbf{X \Lambda} \mathbf{X}^{-1}$
   • $\mathbf{A}$는 Square matrix이고 diagonalize한다면, eigenvector matrix $\mathbf{X}$와 eigenvalue로 이루어진 diagonal matrix인 $\mathbf{\Lambda}$로 분해할 수 있다.
   • 단, $\mathbf{X}$는 orthogonal matrix가 아닐 수 있고, 모든 행렬에서 diagonalize가 가능한 것은 아니다.
4. Orthogonal Diagonalization (for symmetric matrices)
   • $\mathbf{S} = \mathbf{Q \Lambda} \mathbf{Q}^{\mathsf{T}}$
   • $\mathbf{S}$는 Symmetric matrix ($\mathbf{S}=\mathbf{S}^\mathsf{T}$)이면, 항상 orthogonal diagnoalization이 가능하다.
   • $\mathbf{Q}$는 $\mathbf{S}$의 Orthonormal eigenvectors로 이루어진 orthonormal matrix이고, $\Lambda$는 $\mathbf{S}$의 eigenvalue들인 $\lambda_1, \dots, \lambda_n$로 이루어진 diagonal matrix이다.
   • 이는 3. Diagonalization의 특수한 경우로, symmetric matrix에서는 eigenvector들이 orthogonal하므로, $\mathbf{X}^{-1}$ 대신 $\mathbf{Q}^\mathsf{T}$가 사용된다.
5. SVD
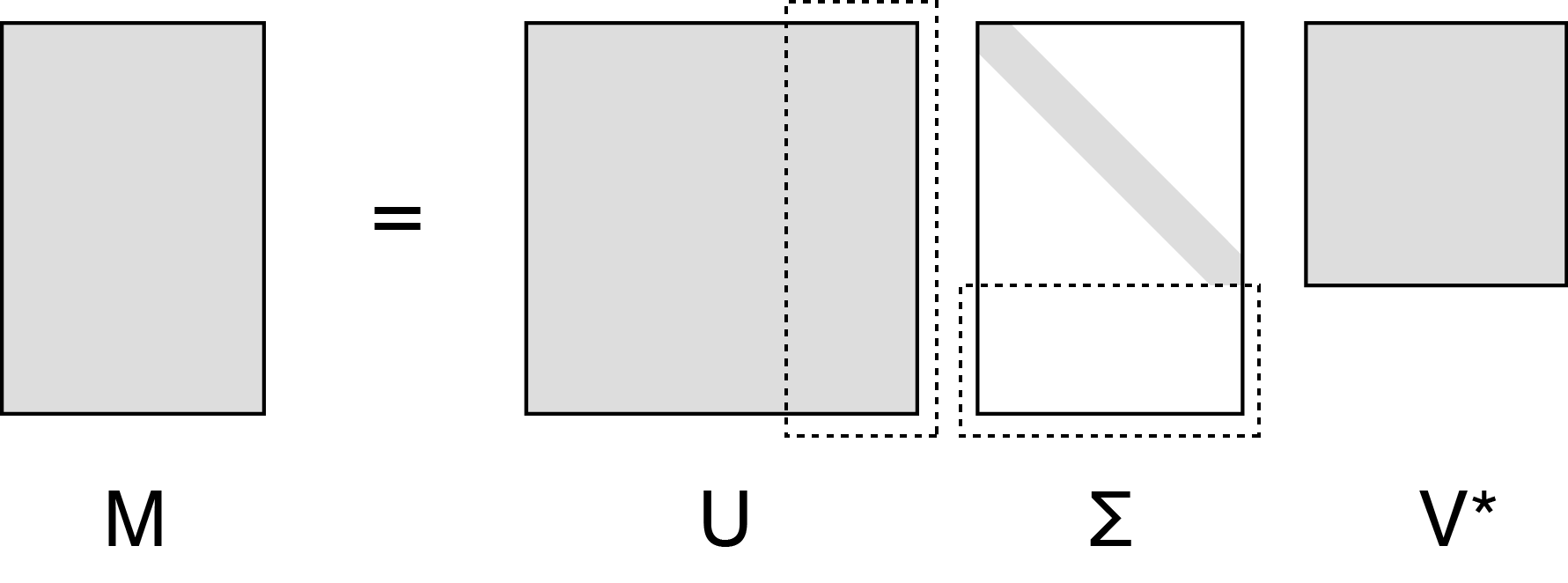
   • $\mathbf{A} = \mathbf{U \Sigma} \mathbf{V}^{\mathsf{T}}$
   • 모든 (square matrix & non-square matrix) 행렬 $\mathbf{A}$에서 항상 성립한다.
   • $\mathbf{U}$와 $\mathbf{V}$는 orthonormal singular vectors들로 이루어진 matrix이고, $\mathbf{\Sigma}$는 singular values들로 이루어진 diagonal matrix이다.
   • SVD는 LU, QR, orthogonal decomposition을 모두 일반화한 경우이다.

Definition of SVD

위에서 본 것처럼 SVD는 아무 Matrix $\mathbf{A}$를 다음과 같이 분해할 수 있음을 뜻한다.

$\mathbf{A} = \mathbf{U \Sigma} \mathbf{V}^{\mathsf{T}}$

이 때 각 행렬은 다음과 같은 특성을 지닌다.

• $\mathbf{U}$: $\mathbf{A}$의 column space를 orthonormal basis(orthornomal singular vectors)로 표현
• $\mathbf{\Sigma}$: Singular value로 이루어진 diagonal matrix
• $\mathbf{V}$: $\mathbf{A}$의 row space를 orthonormal basis(orthornomal singular vectors)로 표현

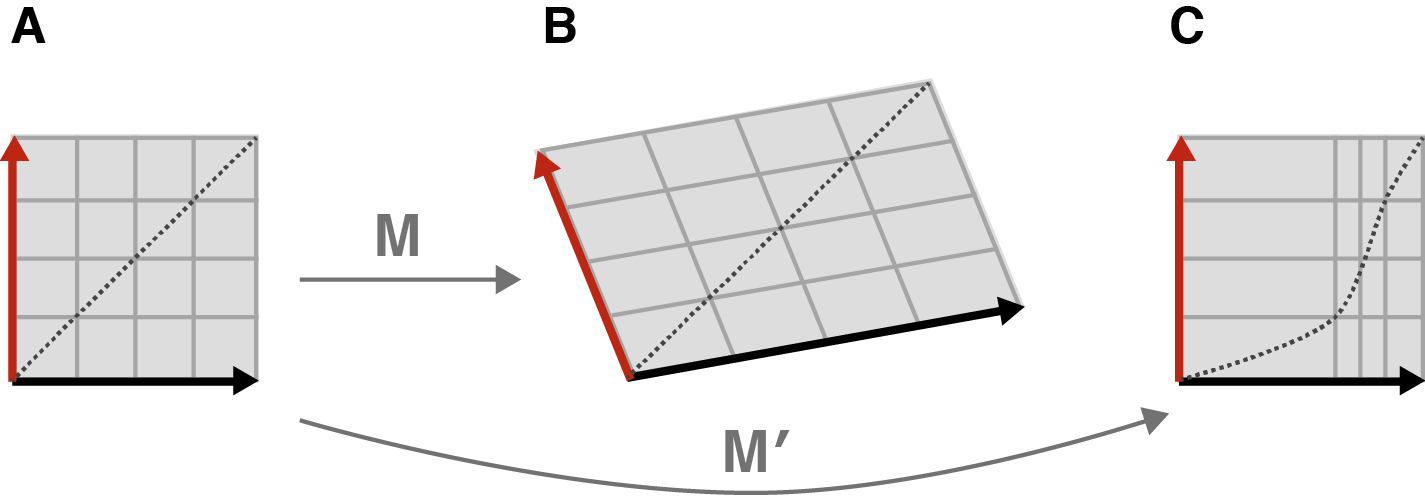
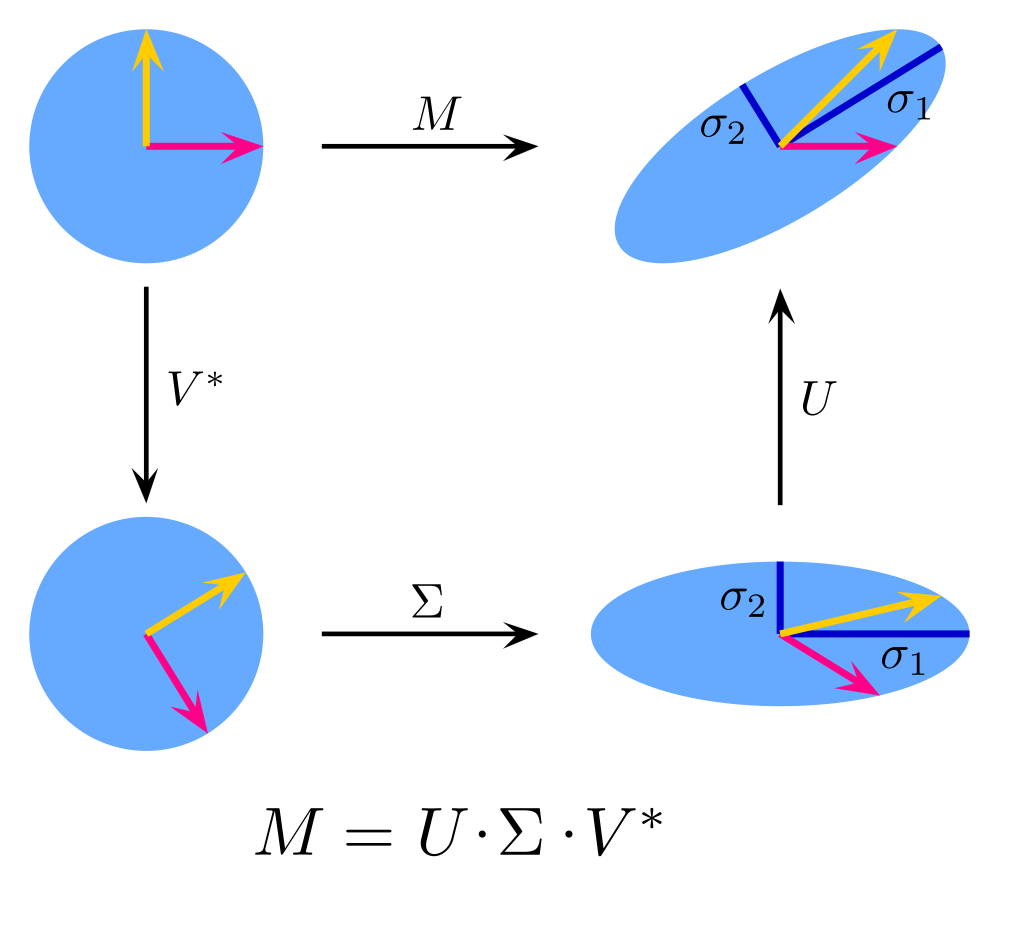
SVD(Singular Value Decomposition)는 모든 행렬을 회전과 스케일링으로 ‘쪼개서’ 이해할 수 있게 해주는 강력한 도구이다. 이는 데이터 압축, 노이즈 제거 등 다양한 분야에서 쓰이기 떄문에 기하학적 해석을 이해해두면 여러모로 유용하다.

Matrix Linear Transformation

2x2 행렬은 평면의 점을 선형 변환(linear transformation)하는 연산자로 볼 수 있다. (A) 늘이기(stretching), (B) 줄이기 (compression), ((C) 회전(rotation), (D) 반사(reflection), (E) 전단(shear)으로 나타낼 수 있다.

Our original square under different types of transformations: (A) stretched, (B) compressed, (C) rotated, (D) reflected or flipped, and (E) sheared

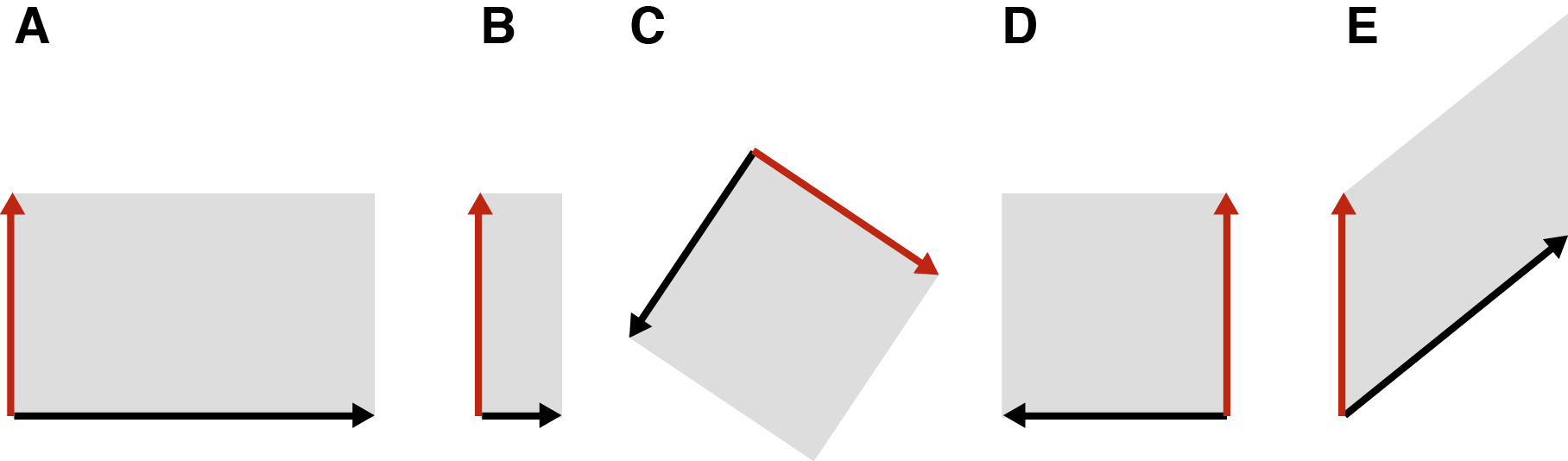
만약 선형이 아니라면, 다음 그림에서 (A)는 (C)처럼 변할 것이다. ((B)는 선형 변환)

(A) Our original square under a linear transformation M (B) and a nonlinear transformation M′(C).

Geometrical interpretations of SVD

여기서 (A) Streching (늘리기): 축 방향으로 길이만 바꿈 (B) Compression (줄이기): 축 방향으로 길이만 바꿈 (C) Rotation (회전): 방향만 바꿈 (길이 보존) (D) Reflection or Flip (반사 혹은 뒤집기): 축 방향으로 방향만 반전 (E) 전단(shear): 한 축을 고정하고 다른 축을 평행이동시켜 모양을 “기울임”

(A)와 (B)는 결국 크기의 문제이지 길이를 바꾸는 “Scaling”관점에서 하나고, (C)와 (D)또한 방향을 바꾼다는 점에서 같은 속성을 지닌다.

(E) 전단(shear)는 직각 구조(Orthogonality)를 깨뜨려 길이와 각도를 바꾸기 때문에, 단순한 회전이나 스케일링보다 다루기 까다롭다. 하지만 모든 Shear 변환도 다음과 같이 Rotation + Scaling + Rotation의 조합으로 표현할 수 있다.

Illustration of the singular value decomposition UΣV⁎ of a real 2 × 2 matrix M.

요약하자면, 모든 행렬(matrix)는 선형 변환이라고 할 수 있고, 이는 Scaling과 Rotation의 조합으로 표현될 수 있다. 그리고 SVD는 임의의 행렬을 ‘회전-스케일링-회전’의 조합으로 분해하는 강력한 방법이다.

Why “Singular”?

기하학적 해석을 통해 SVD는 회전($\mathbf{V}^\mathsf{T}$) ➜ 확대/축소($\Sigma$) ➜ 회전($\mathbf{U}$)의 세 단계로 분해된다는 것을 알 수 있었다.

• Singular value ($\sigma_i$): $\Sigma$ 행렬의 대각 성분으로, 각 축 방향으로 얼마나 확대 또는 축소되는지를 나타내는 ‘배율’
• Right singular vectors ($v_i$): 확대/축소되기 전의 입력 벡터 방향(축)
• Left singular vectors ($u_i$): 확대/축소되기 전의 입력 벡터 방향(축)

만약 Singular value $\sigma_i$가 $0$이라면, 변환 배율이 0이라는 소리이고, 해당 축 방향의 모든 정보는 소멸된다는 것을 의미한다. 즉 3차원이었던 정보가 2차원 혹은 1차원으로 변환되게 된다.

이 경우 행렬은 non-intertible 상태가 되며 singular point가 생기기 때문에 SINGULAR이라는 명칭을 붙였다.

만약 총 $n$개 singular values가 있고, $r$개가 nonzero singular values라고 할 때, 이들을 다음과 같이 내림차순으로 정렬한다고 하자.

\[\begin{align*} \sigma_1 &\geq \sigma_2 \geq \cdots \sigma_r \geq 0 \\ \sigma_{r+1} &= \sigma_{r+2} = \cdots \sigma_n = 0 \end{align*}\]

그러면 다음과 같이 $\mathbf{A}v = \sigma u$를 만족한다.

\[\begin{align*} \mathbf{A}v_1 &= \sigma_1 u_1 \\ \mathbf{A}v_2 &= \sigma_1 u_2 \\ &\cdots \\ \mathbf{A}v_r &= \sigma_1 u_r \\ \mathbf{A}v_{r+1} &= 0 \\ \mathbf{A}v_{r+2} &= 0 \\ &\cdots \\ \mathbf{A}v_{n} &= 0 \\ \end{align*}\]

Matrix form으로는 다음과 같다.

The canonical diagram of the SVD decomposition of a matrix M

참고로 $\mathbf{V}$와 $\mathbf{U}$는 orthogonal하므로, $\mathbf{V}^\mathsf{T}=\mathbf{V}^{-1}$와 $\mathbf{U}^\mathsf{T}=\mathbf{U}^{-1}$를 만족한다.

\[\begin{align} \mathbf{AV_r} &= \mathbf{U_r} \Sigma_r \qquad \\ \overset{m \times n}{\left[ A \right]} \overset{n \times n}{\begin{bmatrix} \, v_1 \; \Big| \; \dots \; \Big| \; v_n \, \end{bmatrix}} &= \overset{m \times m}{\begin{bmatrix} \, u_1 \; \Big| \; \dots \; \Big| \; u_m \, \end{bmatrix}} \overset{m \times n}{ \left[ \begin{array}{ccc|c} \sigma_1 & & & 0 \\ & \ddots & & \vdots \\ & & \sigma_r & 0 \\ \hline 0 & \cdots & 0 & 0 \end{array} \right] } \end{align}\]

여기서는 $\Sigma$가 square matrix라는 보장이 없지만, $\Sigma$에서 0부분을 전부 제거하면 square matrix가 되고 rank $r$에 대해 The reduced form of SVD가 된다.

\[\begin{align} \mathbf{AV} &= \mathbf{U} \Sigma \qquad \\ \overset{m \times n}{\left[ A \right]} \overset{n \times r}{\begin{bmatrix} \, v_1 \; \Big| \; \dots \; \Big| \; v_r \, \end{bmatrix}} &= \overset{m \times r}{\begin{bmatrix} \, u_1 \; \Big| \; \dots \; \Big| \; u_r \, \end{bmatrix}} \overset{r \times r}{ \left[ \begin{array}{ccc} \sigma_1 & & \\ & \ddots & \\ & & \sigma_r \\ \end{array} \right] } \end{align}\]

Proof of SVD Existence

SVD는 과연 모든 matrix에 존재하는가?에 대한 증명을 우선하고자 한다.

우선 Symmetric matrix $\mathbf{S} \in \mathcal{R}^{n \times n}$ 에 대해서 위에서 살펴봤던 Orthogonal Diagonalization (for symmetric matrices)이 성립한다. 실은 이것을 Spectrum theorem이라고 한다. \(\mathbf{S} = \mathbf{Q \Lambda} \mathbf{Q}^{\mathsf{T}}\)

이 증명의 큰 틀은 임의의 $\mathbf{M} \in \mathbb{R}^{m \times n}$를 spectrum theorem을 적용하여 SVD form을 구하는 것이다.

$\mathbf{M}$의 rank을 $r$이라고 하면, $\mathbf{M}^\mathsf{T} \mathbf{M}$는 symmetric matrix가 되고, positive semidefinite matrix $(x^\mathsf{T} A x \geq 0)$이다.

참고로 Positive semidefinite matrix은 다음과 같이 quadaratic form에 의해 증명된다. \(\begin{align} x^\mathsf{T} \mathbf{M}^\mathsf{T} \mathbf{M} x = (Mx)^\mathsf{T} (Sx) = \| Mx \|^2 \geq 0 \end{align}\)

Positive semidefinite matrix는 diagnoalize되며 spectrum theorem에 의해 eigenvalue decomposition이 가능하다.

\[\mathbf{\mathbf{M}^\mathsf{T} \mathbf{M}} = \mathbf{\mathbf{V} \mathbf{\Lambda}} \mathbf{\mathbf{V}}^{\mathsf{T}} = \sum_{i=1}^n \lambda_i v_i v_i^{\mathsf{T}} = = \sum_{i=1}^n (\sigma_i)^2 v_i v_i^{\mathsf{T}}\]

이 때, $\mathbf{V}$의 컬럼은 $\mathbf{M}^\mathsf{T} \mathbf{M}$의 eigenvectors들이며 orthonormal matrix이고, $r \leq n$일 때, $r = \textrm{rank}(\mathbf{M}) = \textrm{rank}(\mathbf{M}^\mathsf{T} \mathbf{M})$이다. 또한, $\sigma_i$는 singular value라고 정의하면 $\sigma_i = \sqrt{\lambda_i}$를 만족한다.

$i$번째의 eigenvector는 다음을 만족한다. (Eigenvalue, Eigenvector 정의: $\mathbf{A} x = \lambda x$)

\[\mathbf{M}^\mathsf{T} \mathbf{M} v_i = (\sigma_i)^2 v_i\]

만약 full rank matrix라면 ($\sigma_i > 0$ for all $i$) 새롭게 $u_i$를 다음과 같이 정의할 수 있다. \(u_i = \dfrac{\mathbf{M} v_i}{\sigma_i}\)

$u_i$는 $\mathbf{M}\mathbf{M}^\mathsf{T}$의 eigenvector인데 이는 다음 식으로 증명될 수 있다.

\[\begin{align} \mathbf{M}\mathbf{M}^\mathsf{T} u_i &= \mathbf{M}\mathbf{M}^\mathsf{T} \left( \dfrac{\mathbf{M} v_i}{\sigma_i} \right) \\ &= \mathbf{M} \left(\mathbf{M}^\mathsf{T} \mathbf{M} \right) \dfrac{v_i}{\sigma_i} \\ &= \mathbf{M} \left( \sigma_i \right)^2 v_i \dfrac{1}{\sigma_i} \\ &= \left( \sigma_i \right)^2 \left(\mathbf{M} v_i \dfrac{1}{\sigma_i} \right) \\ &= \left( \sigma_i \right)^2 u_i \\ \end{align}\]

즉 정리하자면

• $\mathbf{V} \in \mathbb{R}^{n \times n}$는 $\mathbf{M}^\mathsf{T} \mathbf{M}$의 orthonormal eigenvectors
• $\mathbf{U} \in \mathbb{R}^{m \times m}$는 $\mathbf{M} \mathbf{M}^\mathsf{T}$의 orthonormal eigenvectors
• $\sigma_i^2 (i \leq r)$는 $\mathbf{M}^\mathsf{T} \mathbf{M}$와 $\mathbf{M} \mathbf{M}^\mathsf{T}$의 nonzero eigenvalues.

따라서 matrix form으로 정리하면

\[\begin{align} \mathbf{U} &= \mathbf{M V \Sigma^{-1}} \\ \mathbf{U} \Sigma &= \mathbf{M V} \\ \mathbf{U} \Sigma \mathbf{V}^{-1} &= \mathbf{M} \\ \mathbf{U} \Sigma \mathbf{V}^{\mathsf{T}} &= \mathbf{M} \\ \mathbf{M} &= \mathbf{U} \Sigma \mathbf{V}^{\mathsf{T}} \end{align}\]

이 떄, singular value가 0인 경우는 일단 제외하고, 나중에 0을 제외한 full rank에 대해서 SVD를 구한다음 0을 추가한다고 생각하면 된다.

이 증명은 이 글의 증명을 충실하게 따랐다. 개인적으로는 가장 직관적이고 쉽게 증명한 글이라고 생각한다.

SVD의 특성들

spectral norm of a matrix

어떤 임의의 matrix $\mathbf{A} \in \mathbf{R}^{m \times n}$의 SVD를 $\mathbf{A} = \mathbf{U \Sigma V^{\mathsf{T}}}$에서 $\sigma_1 \geq \sigma_2 \geq \cdots$라 하자.

그러면 다음과 같이 spectral norm $\left( \dfrac{| \mathbf{A}x |}{| x |} \right)$ 최대는 $x=v_1$ (첫번쨰 right singular vector)에서 달성된다.

\[\begin{align} \max_{x\neq 0} \dfrac{\| \mathbf{A}x \|}{\| x \|} = \sigma_1 \end{align}\]

증명은 다음과 같다.

\[\dfrac{\| \mathbf{A}x \|^2}{\| x \|^2} = \dfrac{x^{\mathsf{T}} \mathbf{A}^{\mathsf{T}} \mathbf{A} x}{x^{\mathsf{T}} x} = \dfrac{x^{\mathsf{T}} \mathbf{S} x}{x^{\mathsf{T}} x}\]

이 때 rayleigh quotient $ \dfrac{x^{\mathsf{T}} \mathbf{S} x}{x^{\mathsf{T}} x} $는 $x_1, \dots, x_n$에 의존하므로 각각의 원소에 대해서 다음과 같이 미분할 수 있다.

\[\begin{align*} \dfrac{\partial}{\partial x_i} \left( x^{\mathsf{T}} x \right) &= \dfrac{\partial}{\partial x_i} (x_1^2 + \cdots + x_i^2 + \cdots + x_n^2) = 2(x)_i \\ \dfrac{\partial}{\partial x_i} (x^{\mathsf{T}} \mathbf{S} x) &= \dfrac{\partial}{\partial x_i} \left( \sum_i \sum_j S_{ij} x_i x_j \right) = 2 \sum_j S_{ij} x_j = 2 (\mathbf{S}x) \end{align*}\]

이 정보를 가지고 $i=1,\dots, n$에 대해 $\dfrac{x^{\mathsf{T}} \mathbf{S} x}{x^{\mathsf{T}} x} $를 미분하고 $x^{\mathsf{T}} x$로 양분을 나누면 다음과 같이 정리된다. \(\begin{align} (x^{\mathsf{T}} x) \dfrac{\partial}{\partial x_i}(x^{\mathsf{T}} \mathbf{S} x) - (x^{\mathsf{T}} \mathbf{S} x) \dfrac{\partial}{\partial x_i} \left( x^{\mathsf{T}} x \right) &= 0 \\ (x^{\mathsf{T}} x) (2 (\mathbf{S}x)_i) - (x^{\mathsf{T}} \mathbf{S} x) 2(x)_i &= 0 \\ 2 \left( (x^{\mathsf{T}} x) \mathbf{S}x - (x^{\mathsf{T}} \mathbf{S} x) x_i \right) &= 0 \\ (x^{\mathsf{T}} x) \mathbf{S}x &= (x^{\mathsf{T}} \mathbf{S} x) x \\ \mathbf{S}x &= \dfrac{(x^{\mathsf{T}} \mathbf{S} x)}{(x^{\mathsf{T}} x)} x \\ \mathbf{S}x &= \lambda x \end{align}\)

이 때 $\lambda := \dfrac{(x^{\mathsf{T}} \mathbf{S} x)}{(x^{\mathsf{T}} x)}$이다.

결국 $\mathbf{S} = \mathbf{A^{\mathsf{T}}A}$의 eigenvalue를 찾는것으로 문제가 좁혀졌고, 이 때의 eigenvalue는 $\lambda_1= \sigma_1^2$이며, eigenvector는 $x=v_1$이다. 첫번쨰 singular value를 구한셈이다.

두번째 singular value부터는 $\left( \dfrac{| \mathbf{A}x |}{| x |} \right)$ 최대를 구하는 같은 문제에 $v_1^{\mathsf{T}} x = 0$ 조건을 넣어서 풀면 된다. 이는 Langrange multiplier에 제약조건($g(x)$)을 넣어서로 풀 수 있다.

\[\begin{align} \mathcal{L}(x_1, \dots, x_n, \lambda) = f(x_1, \dots, x_n) - \lambda (g(x_1, \dots, x_n) - c) \end{align}\]

Singular vector of $\mathbf{A}^\mathsf{T}$

SVD는 $\mathbf{A} = \mathbf{U \Sigma V^{\mathsf{T}}}$를 통해 $v$의 row space(입력)를 $u$의 column space(출력)으로 연결시켜주는 역할을 한다. $\mathbf{A}^\mathsf{T} = \mathbf{V \Sigma^{\mathsf{T}} U^{\mathsf{T}}}$에서는 반대로 $u$의 row space를 $v$의 column space로 연결시킨다.

SVD of symmetric block matrix

\(\mathbf{S} = \begin{bmatrix} 0 & \mathbf{A} \\ \mathbf{A}^{\mathsf{T}} & 0 \end{bmatrix}\) 는 $r$개의 pair positive / negative eigenvalue를 가지게 되고 다음과 같은 $(m+n,)$의 크기를 가지는 eigenvector들을 가지게 된다. \(\begin{bmatrix} u_k \\ v_k \end{bmatrix}, \begin{bmatrix} -u_k \\ v_k \end{bmatrix}\)

AB and BA

$\mathbf{A} \in \mathbb{R}^{m \times n}, \mathbf{B} \in \mathbb{R}^{n \times m}$이면, $\mathbf{AB}$와 $\mathbf{BA}$는 같은 eigenvalue를 가지게 된다. 증명은 매우 심플한데, $ABx = \lambda x, BAB x = \lambda Bx,BA (Bx) = \lambda (Bx) $이기 때문에 $Bx$를 하나의 vector $y$라고 생각하면 eigenvalue의 정의에 따라 증명된다. $Bx$가 eigenvector가 되는건 덤이다.

References

• A Geometrical Understanding of Matrices
• Singular Value Decomposition as Simply as Possible
• Singular Value Decomposition Part 1: Perspectives on Linear Algebra
• SVD分解(一)：自编码器与人工智能
• 低秩近似之路（二）：SVD
• SVD的导数
• Transformations in a Plane

1. Strang, Gilbert, and others. 2019. Linear Algebra and Learning from Data. Vol. 4. Wellesley-Cambridge Press Cambridge.