Preventing Overfitting with Norms and Batch Normalization

Introduction

머신러닝의 궁극적인 목적은 무엇일까? 그것은 일반화(generalization)이다. 훈련 데이터의 학습을 통해 시그널(signal) 혹은 패턴(pattern)을 학습해, 처음 보는 데이터에 대해서도 정확한 예측을 해내는 것을 요구한다.

하지만 모델은 종종 엉뚱한 길로 빠진다. 진짜 패턴을 넘어 데이터에 섞인 ‘노이즈(Noise)’까지 통째로 암기(Memorization)해버리는 경우가 종종 있다. 이처럼 훈련 데이터는 완벽하게 외웠지만 실전에서는 성능이 하락하는 현상을 과적합(Overfitting)이라 부른다.

최근 몇 년간 Double descent, grokking, memorization vs. generalization까지 이어지는 논문들의 흐름에서 기존 전통적인 머신러닝 이론에서의 오버피팅이라는 단어는 새롭게 재정의되고 있다. 오버피팅이 단순한 훈련/테스트 성능 곡선을 넘어, ‘암기’와 ‘일반화’ 사이의 치열한 싸움임을 보여주고 있다.

과적합의 근본적인 원인은 모델 복잡도 제어 실패에 있다. 모델의 복잡도를 적절히 제어하면, 모델은 ‘노이즈’처럼 사소하고 특이한 정보는 무시하고, 데이터 전체를 관통하는 중요하고 반복적인 ‘패턴’에만 집중하게 되어 일반화에 성공한다. 그러나, 모델이 너무 복잡하면(자유도가 높으면) 노이즈까지 암기해버리고, 이는 곧 일반화의 실패로 이어진다.

따라서 이 글에서는 일반화(generalization)라는 최종 목표를 달성하기 위해, 모델 복잡도를 측정하는 수학적 도구인 Norm부터 시작하여, 이를 제어하는 정규화(Regularization) 기법들을 거쳐, 궁극적으로 일반화 성능을 어떻게 향상시킬 수 있는지에 대해 설명하고자 한다.

Generalization Error

우선 첫번쨰 해야할 질문은 “기계가 데이터를 통해 학습하는 것이 과연 가능한가?”이다. 한정된 훈련 데이터셋(sample)만을 가지고 있을 때, 여기서 얻은 훈련 오차 ($E_{in}$)가 일반화 오차 ($E_out$)와 비슷할 것이라고 어떻게 장담할 수 있을까?

Learning Feasibility

위 질문은 다음과 같이 2개의 문제로 분류할 수 있다. 어떤 모델 혹은 hypothesis $g$가 있다고 하자.

1. 일반화 오차를 훈련오차와 가깝다고 어떻게 확신할 수 있을까? (일반화 문제) ($E_{out}(g) \approx E_{in}(g)$)
2. 훈련 오차를 충분히 작게만들 수 있을까? (최적화 문제) $E_{in}(g) \approx 0$

우선 2.는 우리에게 주어진 모델 후보들 중에서 실제로 훈련 데이터를 가장 잘 설명하는 모델을 찾아낼 수 있느냐의 문제이고 답은 현재 가지고 있는 여러 모델들을 학습시키는 방법으로 훈련하면 된다이다. 이건 최적화(Optimization)문제라고 할 수 있다. Ordinary Least Squares를 푸는 방법부터 시작해서 딥러닝에서 쓰는 Gradient descent같은 방법이 그 예이다. 하지만 모든 모델이 다 작동하는건 아니다. 어떤 모델은 훈련 오차를 작게 만드는데 실패하기도 한다. 즉, 이건 보장할 수 없다.

1.은 우리가 $E_{in}(g)$를 얼마나 신뢰하며, 실제($E_{out}(g)$)에서도 비슷할 것이라고 말할 수 있는가?에 대한 문제이다. 이에 대한 답은 호프딩 부등식(Hoeffding’s inequality)이다.

Hoeffding’s inequality

최종 목표 hypothesis $g$에 대한 $E_{out}(g) \approx 0$은 확인할 방법은 없다. 실제 target function $f$는 모를 것이다. 그러나 $E_{in}(g)$는 알 수 있다. 이걸 호프딩의 부등식(Hoeffding’s inequality)을 통해 교환할 수 있다.

1. 최종 목표: $E_{out}$을 낮추는 것.
2. 호프딩의 부등식: $E_{out}$은 $E_{in}$과 비슷할 확률이 높다.
3. 실행 계획 (교환): 그러므로 우리가 할 수 있는 $E_{in}$을 낮추는 데 집중하자! 그러면 높은 확률로 $E_{out}$도 낮아질 것이다.

호프딩의 부등식은 확률론에 기반하여 “샘플의 평균은 실제 전체의 평균과 비슷할 확률이 높다”는 것을 수학적으로 보장한다. 충분한 양의 데이터를 샘플링했다면, 훈련 오차($E_{in}(g)$)가 일반화 오차($E_{out}(g)$)와 크게 다르지 않을 것이라 말해준다.

\[\begin{equation} \mathbb{P} ( | E_{in}(g) - E_{out}(g)| > \epsilon ) \leq 2M e^{-2\epsilon^2 N} \end{equation}\]

각각 term의 의미는 다음과 같다.

• $E_{in}(g)$: 훈련 데이터셋에서의 오차 (in-sample error)
• $E_{out}(g)$: 전체 데이터 분포에 대한 실제 오차 (out-of-sample error)
• $\epsilon$: 허용 오차 한계 (tolerance)
• $M$: 가설 집합(Hypothesis set, $\mathcal{H}$) 안에 있는 가설(모델)의 개수
• $N$: 훈련 데이터 개수

Hoeffding’s inequality를 통해 두가지 사실을 알 수 있다.

첫 번쨰는 일반화 문제(1)에서는 실제 target function $f$는 전혀 중요하지 않다는 것이다. $f$는 무엇인지 절대 알 수 없고 통제할 수 있는 대상도 아니라는 것이다. 다만, $f$의 문제는 최적화 문제(2)에서는 문제가 될 수 있다. 복잡한 $f$ 일수록, 학습하기가 힘들어지기 때문이다. 이는 Hoeffding’s inequality는 최적화 문제(2)에 답을 줄 수가 없다라는 사실과 일맥상통한다.

두 번째 사실은 가설 집합 ($\mathcal{H}$)의 복잡도는 다음과 같은 trade-off를 던져준다.

1. 일반화(Generalization, (1)) 관점:
   • $\mathcal{H}$는 단순할수록 좋다.
   • 이는 $M$이 작을 수록 hoeffding’s inequality의 우변이 작아지기 때문에 말이 된다.
2. 최적화(Optimization, (2)) 관점:
   • $\mathcal{H}$는 복잡할수록 좋다.
   • 이는 $g$의 후보군을 늘려줘서 더 적은 오차를 생성할 $g$를 찾아낼 확률을 높아내기에 좋다.

여기서의 $M$ 즉 Complexity of $\mathcal{H}$이 모델 복잡도이며, 이 글에서 주요 주제로 다룰 주제이다.

Generalization Error Bound

Hoeffding’s inequality식을 역으로 풀어서 오차경계 즉, Generalization Error Bound를 구할 수 있다. 즉, 신뢰도(confidence)를 얻으려면, 감수해야 할 오차의 한계($\epsilon$)가 얼마인가?에 대한 답이라고 할 수 있다.

이는 가장 피하고 싶은 상황 즉, 훈련 오차($E_{in}(g)$)와 실제 오차($E_{out}(g)$)의 차이가 클 확률을 Hoeffding’s inequality를 통해 얼마나 작은지 (bounded) 제한하여 알려주는 것이다.

우선 도입해야할 것은 신뢰도 $\delta$이다. $\delta$는 감수할 수 있는 위험의 크기이다. $\delta=0.05$라고 하면 5%의 위험을 감수하고, 95%의 신뢰도를 원한다는 의미인 것이다.

\[P(\textrm{Bad Event}) \leq \delta\]

그리고 $\delta$로부터 $\epsilon$은 다음과 같이 구할 수 있다.

\[\begin{align} \mathbb{P} ( | E_{in}(g) - E_{out}(g)| > \epsilon ) &\leq 2M e^{-2\epsilon^2 N} \\ \mathbb{P} ( | E_{in}(g) - E_{out}(g)| > \epsilon ) &\leq \delta \\ \delta &:= 2M e^{-2\epsilon^2 N} \\ \dfrac{\delta}{2M} &= e^{-2\epsilon^2 N} \\ \ln{\left(\dfrac{\delta}{2M}\right)} &= -2 \epsilon^2 N \\ \ln{\left(\dfrac{2M}{\delta}\right)} &= 2 \epsilon^2 N \\ \epsilon^2 &= \ln{\left(\dfrac{2M}{\delta}\right)} \dfrac{1}{2N} \\ \epsilon &= \sqrt{\dfrac{1}{2N} \ln{\left(\dfrac{2M}{\delta}\right)} } \\ \end{align}\]

이렇게 구한 $\epsilon$으로 $E_{in}(g)$와 $E_{out}(g)$을 넣으면 $1-\delta$의 확률로 다음을 만족함을 알 수 있다.

\[\begin{equation} E_{out}(g) \leq E_{in}(g) + \sqrt{\dfrac{1}{2N} \ln{\left(\dfrac{2M}{\delta}\right)} } \end{equation}\]

즉 $1-2M e^{-2\epsilon^2 N}$의 확률로 우리가 원하는 훈련 오차와 실제오차가 작을 확률인 $| E_{in}(g) - E_{out}(g)| \leq \epsilon$를 만족한다는 것이고, 이는 $E_{out}(g) \leq E_{in}(g) + \epsilon$을 만족하며, 이 때 $\epsilon = \sqrt{\dfrac{1}{2N} \ln{\left(\dfrac{2M}{\delta}\right)} }$을 만족한다는 것을 알 수 있다.

Effective Number of Hypothesis

문제점은 가설공간의 크기 $M$은 무한(infinite)이 될 수 있다는 점이다. 이러면 $\epsilon$이 아무 의미가 없어진다. 하지만 실제로 모든 $M$개의 가설이 필요한 것이 아니다. 실제로 유효한 (effective) 가설의 개수만 세면 된다. 이를 위해 성장 함수(growth function)을 도입하여 $M$ 대신 $m_{\mathcal{H}} (N)$으로 대체한다.

growth function을 도입한 이유는 실제로 M개가 있다고 해도 그 중에서 중복도 많을 것이고, 실제 유효한 가설은 데이터의 개수 $N$에 영향을 받을 것이라는 가정이 담긴 함수이다.

정리하면 가설 공간(Hypothesis Set) $\mathcal{H}$에 대해서 다음과 같이 growth function $m_{\mathcal{K}} (N)$을 정의할 수 있다. 이 때 $| \dot |$은 set의 cardinality를 의미하며, 집합의 원소의 개수를 의미하는 기호이다.

\[\begin{equation} m_{\mathcal{H}}(N) = \max_{x_1, \cdots, x_N \in \mathcal{X}} | \mathcal{H}(x_1, \cdots, x_N) | \end{equation}\]

$M$과 $m_{\mathcal{H}} (N)$의 차이는 $\mathcal{X}$의 전체를 보느냐 아니면, $N$ points에 한정해서 보느냐의 차이이다.

Binary classification에서는 가설공간이 가질 수 있는 값은 $\lbrace -1, +1 \rbrace$ 이렇게 두가지 뿐이다. (Abu-Mostafa, Magdon-Ismail, and Lin 2012) 에서는 이를 dichotomics(이분법)이라고 표현한다. 그러면 $N$개의 data points에 대해서 총 $2^N$개의 경우의 수가 생긴다. 따라서 dichotomics에서는 $m_{\mathcal{H}}(N)$은 다음과 같이 bound된다.

\[m_{\mathcal{H}}(N) \leq 2^N\]

물론 $2^N$도 작은 수는 아니겠지만, 무한대($\infty$)보다는 유한한 값이므로 개선된 결과이다. 즉 무한한 $M$을 제한하기 위해, 가설 집합의 복잡도를 측정하는 방식을 가설의 총개수에서 $N$개의 데이터에 대한 표현력으로 바꾸는 방법이다.

하지만 지수적인 것을 더 줄일 수는 없을까?

Break Point

실제로는 모든 경우의 수를 다 고려할 필요는 없다. 왜냐하면 linear classifier라고 가정했을 때 표현이 불가능한 조합도 있기 때문이다.

예를 들어 $m_{\mathcal{H}}(3)$은 다음 두 경우 때문에 $2^3=8$이 아닌 6이 된다.

mH(3)

$m_{\mathcal{H}}(4)$ 또한 다음 두 경우 때문에 $2^4=16$이 아닌 14가 된다.

mH(4)

이 때 break point $k$는 다음과 같이 정의할 수 있다.

If no data set of size $k$ can be shattered by $\mathcal{H}$, then $k$ is said to be a break point for $\mathcal{H}$

여기서 “shattered”라는 말이 이해하기가 쉽지 않았는데, 한글로는

어떻게 $k$개의 데이터 포인트를 가져와 배치하더라도 가설 집합 $\mathcal{H}$가 모든 가능한 분류 패턴($2^k$개)을 만들어낼 수 없다면, 이 $k$를 $\mathcal{H}$의 break point(브레이크 포인트)라고 한다.

그리고 수학적인 증명은 생략하겠지만, $k$가 존재한다면, $m_{\mathcal{H}}(k) < 2^k$가 되고

\[\begin{equation} m_{\mathcal{H}}(N) \leq \sum_{i=0}^{k-1} \begin{pmatrix} N \\ i \end{pmatrix} \end{equation}\]

가 되고, 이는 $N$에 대한 $k-1$차 다항식(polynomial)이다. 지수함수 $2^N$이 다항함수로 줄어든 것이다!

위의 그림을 다시 살펴보면, 3개의 점이 일직선(colinear)상에 있으면 (+1, -1, +1) 혹은 (-1, +1, -1) 조합은 분류할 수 없는 것이다. 그러나, 삼각형 모향으로 배치하면 3개의 점으로는 모든 linear classifier가 동작하게 된다. 즉 3은 break point가 될 수 없다.

그러나 4개의 포인트를 가정해보자. 4개의 포인트는 위 그림처럼 XOR패턴이 아니더라도 어떤방식으로든 저 데이터셋에서는 모델로 분류할 수 있는 모든 패턴을 만들 수 없다. 이런 경우 break point $k=4$가 된다.

단 하나의 배치에서라도 shatter(주어진 위치에 있는 포인트들에 대해 모델이 모든 분류 패턴을 만들기)에 실패하는 것만으로는 부족하고, 가능한 모든 배치에서 shatter가 불가능해야 break point를 정의할 수 있다.

VC Dimension

VC Dimension은 The Vapnik-Chervonenkis dimension의 줄임말이며, $d_{vc}(\mathcal{H})$이라고 한다. $d_{vc}$는 Break point $k$와 $k = d_{vc} + 1$의 관계를 가진다. break point $k$는 shatter가 실패하는 데이터 포인트 수를 나타냈다면, $d_{vc}$는 모델이 다룰 수 있는 최대의 데이터 포인트를 나타낸다.

VC dimension은 결국 모델이 얼마나 다양한 데이터를 ‘깨뜨릴(shatter)’ 수 있는지에 대한 조합론적(combinatorial) 척도라고 할 수 있다.

VC dimension은 모델이 어디까지 가능한가?를 나타내주는 단위이며, 모델이 가진 자유도(degrees of freedom)나 표현력(expressive power)을 직접적으로 나타내기 때문에 break point보다 더 선호된다.

VC Generalization Bound

이를 이용하여 $m_{\mathcal{H}}(N)$를 다시 작성하면 다음과 같고

\[\begin{equation} m_{\mathcal{H}}(N) \leq \sum_{i=0}^{d_{vc}} \begin{pmatrix} N \\ i \end{pmatrix} \end{equation}\]

귀납법을 통해 더 유용하게 다음과 같이 표현된다.

\[\begin{equation} m_{\mathcal{H}}(N) \leq N^{d_{vc}} + 1 \end{equation}\]

이 VC dimension은 기존 Error bound의 문제를 획기적으로 해결할 수 있다. 원래의 이 식을

\[\begin{equation} E_{out}(g) \leq E_{in}(g) + \sqrt{\dfrac{1}{2N} \ln{\left(\dfrac{2M}{\delta}\right)} } \end{equation}\]

아래와 같이 만들고, $\ln$과 $1/N$덕분에 $N$이 크다면 매우 작은 값으로 수렴하게 된다. 따라서 $E_{out}(g) \approx E_{in}(g)$가 가능해지는 것이다. \(\begin{equation} E_{out}(g) \leq E_{in}(g) + \sqrt{\dfrac{1}{2N} \ln{\left(\dfrac{2 m_{\mathcal{H}}(2N)}{\delta}\right)} } \end{equation}\)

근데 왜 $m_{\mathcal{H}}(N)$이 아니라 $m_{\mathcal{H}}(2N)$인 것인가?

그것은 $E_{out}(g)$은 데이터셋이 무한이기 때문에 비교하기가 쉽지 않기 떄문이다. 그래서 $E_{in}(g)$의 데이터셋을 $\mathcal{D}$라고 하면, 동일한 분포의 같은 크기의 데이터셋인 $\mathcal{D’}$을 만들고 $E_{in}(g)$ in $\mathcal{D}$와 $E_{in}(g)$ in $\mathcal{D’}$를 비교하는 문제로 바꿔서 해결하고자 한다. 따라서 두 데이터셋 $\mathcal{D}$와 $\mathcal{D}’$ 각각의 크기인 $N$을 합쳐서 $2N$에 대하여 growth function을 $m_{\mathcal{H}}(2N)$로 사용한다.

여기서 중요한 가정은 동일한 분포의 데이터셋이라는 것이다. train set과 test set이 동일한 분포가 아니면 $E_{out}(g) \approx E_{in}(g)$은 성립될 수 없다는 머신러닝의 기본적인 가정이 여기에서 나오는 것이다.

최종적으로는 VC Generalization Bound는 일부 상수가 조정되어 다음과 같이 표현된다.

\[\begin{equation} E_{out}(g) \leq E_{in}(g) + \sqrt{\dfrac{8}{N} \ln{\dfrac{4m_{\mathcal{H}}(2N)}{\delta}} } \end{equation}\]

그리고 이를 VC dimension $d_{vc}$를 포함하면 다음과 같이 된다.

\[\begin{equation} E_{out}(g) \leq E_{in}(g) + \sqrt{\dfrac{8}{N} \ln{\dfrac{4 ((2N)^{d_{vc}} + 1) }{\delta}} } \end{equation}\]

Rademacher Complexity

Lessons from VC dimension

지금까지 모델의 복잡도에 대해 알아봤다. Generalization Bound를 다시한번 간단하게 표현하면 다음과 같다.

\(\begin{equation} \textrm{Test error} \leq \textrm{Train error} + \mathcal{O}(\textrm{Model Complexity}) \end{equation}\) 우리의 목표인 Train error와 Test error의 격차를 줄이려면 Model Complexity를 최대한 억제해야함을 알 수 있었고, 이를 VC dimension을 통해 컨트롤할 수 있음을 알았다.

VC dimension은 이론적으로는 훌륭하다. 그러나, 현실적으로 복잡한 모델의 complexity를 vc dimension을 통해 구할 수 없다. 왜냐하면 VC dimension은 단순한 binary classificatiion을 기준으로 계산한 것이기 떄문이다. SVM만 되어도 VC dimension을 구하기가 매우 어려워진다.

또한 VC dimension은 worst case인 경우를 가정하기 때문에 모든 데이터 포인트를 생각해서 계산해야한다. 그래서 데이터가 간단한 분포를 따르더라도 VC dimension은 변하지 않는다. VC dimension은 데이터의 ‘분포’나 ‘배치’와는 무관하게 최악의 경우를 가정하기 때문이다.

따라서 데이터 분포를 고려한 새로운 모델 복잡도가 필요한 시점이다.

What is Rademacher Complexity?

이렇게 등장하는것이 Rademacher Complexity이다. Rademacher Complexity는 만약 어떤 모델이 완전한 무작위 노이즈(random noise)에도 잘 들어맞는다면, 그 모델은 매우 복잡하고 과적합될 위험이 높다 라는 가정에서 시작한다.

(Mohri, Rostamizadeh, and Talwalkar 2018)에서는 이를 Empirical Rademacher Complexity라고 정의한다. 기존 hypothesis set $\mathcal{H}$대신에 특정 loss function $L: \mathcal{y} \times \mathcal{y} \rightarrow \mathbb{R}$을 정의하고 $\mathcal{Z} = \mathcal{X} \times \mathcal{Y}$위에서의 loss function들의 집합을 $\mathcal{g}$라고 정의한다.

\[\begin{equation} \mathcal{g} = \lbrace g: (x, y) \mapsto L(h(x), y): h \in \mathcal{H}\rbrace \end{equation}\]

이를 일반화하여 $\mathcal{g}$를 $\mathcal{Z} \mapsto [a, b]$에 해당하는 함수들의 집합, $S = (z_1, \cdots, z_m)$을 m개의 샘플링된 $\mathcal{Z}$라고 가정한다. 이 때 Empirical Rademacher Complexity는 다음과 같다.

\[\begin{equation} \widehat{\mathfrak{R}}_S(\mathcal{G}) = \mathbb{E}_{\mathbf{\sigma}} \left[ \sup_{g \in \mathcal{G}} \dfrac{1}{m} \sum_{i=1}^{m} \sigma_i g(z_i) \right], \end{equation}\]

이 때 $\mathbf{\sigma} = (\sigma_1, \dots, \sigma_m)^{\mathsf{T}}$이고, $\sigma_i$는 $\lbrace -1, +1 \rbrace$로 중 추출된 independent uniform random variables이다.

즉 위에서 말한대로 데이터 샘플($S$)에 대해 모델 집합($\mathcal{g}$)이 얼마나 잘 끼워맞출 수 있는가를 평균적으로 측정한 값이다.

이를 내적의 형태로는 다음과 같이 쓸 수도 있다.

\[\begin{equation} \widehat{\mathfrak{R}}_S(\mathcal{G}) = \mathbb{E}_{\mathbf{\sigma}} \left[ \sup_{g \in \mathcal{G}} \dfrac{\mathcal{\mathbb{\sigma}}\mathcal{\mathbb{g}_S}}{m} \right], \end{equation}\]

Empirical Rademacher Complexity를 일반화하여 특정 샘플 $S$가 아닌 샘플링 과정 전체에 대한 복잡도를 기대값으로 표현할 수 있다. 그것이 Rademacher Complexity의 정의이다.

$\mathcal{D}$를 데이터 분포라고 하자. $S$는 $\mathcal{D}$로 추출된 특정 샘플링(샘플링 사이즈는 $m$)이라고 했을 때, 여러번 샘플링을 반복한 Empirical Rademacher Complexity을 Rademacher Complexity라고 하며 다음과 같이 정의한다.

\[\begin{equation} \mathfrak{R}_m(\mathcal{G}) = \mathbb{E}_{S \sim \mathcal{D}^m} \left[ \widehat{\mathfrak{R}}_S(\mathcal{G}) \right] \end{equation}\]

두 Rademacher Complexity의 차이는 다음과 같다.

• Empirical Rademacher Complexity
  • $\widehat{\mathfrak{R}}_S(\mathcal{G})$
  • 특정 샘플 S에서 측정한 복잡도
  • 주어진 학습 데이터로 측정된 오차 (train error) 혹은 표본 평균
  • 이번에 뽑은 데이터셋 기준으로 모델 클래스가 얼마나 복잡한가?
  • 랜덤 노이즈 $\sigma$에 의존
• Rademacher Complexity
  • $\mathfrak{R}_m (\mathcal{G})$
  • 샘플링 과정 전체에 대한 기대 복잡도
  • 실제 데이터에 대한 복잡도 오차 (test error) 혹은 모평균
  • 데이터를 여러 번 무작위로 뽑는다면, 평균적으로 모델 클래스가 얼마나 복잡할까?
  • 랜덤 노이즈 $\sigma$와 샘플링된 데이터셋 $S$에 의존

Generalization bounds based on Rademacher Complexity

Rademacher Complexity에 기반한 Generalization bounds은 다음과 같다.

$\mathcal{G}$를 $\mathcal{Z} \mapsto [0, 1]$의 매핑이라고 하자. $m$의 크기로 $S$로부터 i.i.d 샘플링했을 때 $g \in S$ 각각에 대해, VC dimension처럼 신뢰도 $\delta$를 사용하면 최소 $1-\delta$의 확률로 다음이 성립한다.

\[\begin{align} \mathbb{E}[g(\mathcal{z})] &\leq \dfrac{1}{m} \sum_{i=1}^m g(z_i) + 2 \mathfrak{R}_m (\mathcal{G}) + \sqrt{\dfrac{\log{\dfrac{1}{\delta}}}{2m}} \\ \mathbb{E}[g(\mathcal{z})] &\leq \dfrac{1}{m} \sum_{i=1}^m g(z_i) + 2 \widehat{\mathfrak{R}}_S (\mathcal{G}) + 3\sqrt{\dfrac{\log{\dfrac{2}{\delta}}}{2m}} \end{align}\]

이것의 증명은 다음과 같다.

함수 클래스 $\mathcal{G}$는 데이터 포인트 $\mathbf{z}$를 입력받아 실수 값을 출력하는 함수 $g$들의 집합이다.
머신러닝 맥락에서 각 함수 $g$는 특정 모델($h$)의 loss function, 즉 $g(\mathbf{z}) = \ell(h(\mathbf{x}), y)$에 해당할 수 있다.

이때, $\mathbb{E}[g]$는 데이터의 실제 분포 $\mathcal{D}$에 대한 $g$의 기대값(진짜 성능)을 의미하며, 이 값을 알 수 없다.

대신 다음과 같이 주어진 샘플 $S = (\mathbf{z}_1, \dots, \mathbf{z}_m)$에 대한 $g$의 경험적 평균(측정된 성능)을 정의할 수 있다.

\[\begin{equation} \widehat{\mathbb{E}}_S [g(\mathcal{z})] := \frac{1}{m} \sum_{i=1}^{m} g(z_i) \end{equation}\]

이 둘의 차이를 $\Phi(S)$라고 하자.

\[\begin{align} \Phi(S) := \sup_{g \in \mathcal{G}} \left( \mathbb{E}[g] - \widehat{\mathbb{E}}_S[g] \right) \end{align}\]

이는 특정 샘플 $S$ 위에서, 함수 클래스 $\mathcal{G}$에 속한 모든 함수 $g$ 중에서, ‘진짜 성능($\mathbb{E}[g]$)’과 ‘측정된 성능($\widehat{\mathbb{E}}_S[g]$)’ 간의 차이(일반화 갭)가 가장 큰 최악의 경우(supremum)가 얼마인지를 나타낸다. 즉, 이 샘플 $S$가 얼마나 우리를 ‘긍정적으로 속일 수 있는지’에 대한 척도이다.

만약 $S$의 포인트 하나만을 달리하는 $S’$를 또 정의할 수 있고 달라지는 샘플을 $S$에서의 $z_m$과 $S’$에서의 $z^{‘}_m$이라고 한다면, supremumd의 차이는 차이의 supremum보다 커질 수 없으므로 (\(|\sup{A} - \sup{B}| \leq \sup{|A-B|}\)) 다음과 같은 관계를 만족한다. 이는 $\mathcal{G}$를 $\mathcal{Z} \mapsto [0, 1]$의 매핑이라고 했기 때문에 차이의 최대가 1이기 때문이다.

\[\begin{align} \Phi(S) - \Phi(S') \leq \sup_{g \in \mathcal{G}} \left( \widehat{\mathbb{E}}_S[g] - \widehat{\mathbb{E}}_{S'}[g] \right) = \sup_{g \in \mathcal{G}} \dfrac{g(z_m) - g(z^{'}_m)}{m} \leq \dfrac{1}{m} \end{align}\]

마찬가지로 $\Phi(S’) - \Phi(S) \leq 1/m$라고 증명할 수 있다. 따라서 $|\Phi(S’) - \Phi(S)| \leq 1/m$이다. 즉 $\Phi(S)$는 bounded difference를 만족한다.

McDiarmid’s Inequality는 이렇게 bounded difference관계가 있을 때 적용할 수 있는 부등식이다. 입력이 조금 변해도 출력이 많이 변하지 않는 함수라면, 그 함수는 집중(concentration)된다는 것이다.

만약 $f(z_1, \dots, z_m)$이 각 입력 $z_i$에 대해, $|f(z_1,\dots,z_i,\dots,z_m) - f(z_1,\dots,z^{‘}_i,\dots,z_m)| \leq c_i$를 만족한다면 (bounded difference), \(P (f(S) - \mathbb{E}[f(S)] \geq t ) \leq \exp{\left( \dfrac{-2t^2}{\sum_{i=1}^m c_i^2}\right)}\)을 만족한다.

여기서 위에서 구한 bounded difference를 조합하여 $\sum_{i=1}^m c_i^2 = m \left( \dfrac{1}{m^2} \right) = \dfrac{1}{m}$을 만족한다.

\(P (f(S) - \mathbb{E}[f(S)] \geq t ) \leq \exp{(-2mt^2)}\) 가 되고 기존 신뢰도 $\delta$를 이용하여 이 확률을 $1 - \delta / 2$라고 가정하면 (변수변환을 위한 단순 교체), 다음과 같이 구할 수 있다.

\[\exp{(-2mt^2)} = \delta / 2 \rightarrow t = \sqrt{\dfrac{\log(2/\delta)}{2}}\]

이 결과를 McDiarmid’s Inequality에 다시 넣어서 정리하면, 다음과 같다. \(\Phi(S) \leq \mathbb{E}_S [\Phi(S)] + \sqrt{\dfrac{\log(2/\delta)}{2}}\)

그리고 $\mathbb{E}_S [\Phi(S)]$은 다음 과정을 통해 Rademacher Complexity로 변환될 수 있다.

\[\begin{align*} \mathbb{E}_S [\Phi(S)] &= \mathbb{E}_S \left[ \sup_{g \in \mathcal{G}} (\mathbb{E}[g] - \widehat{\mathbb{E}}_S[g]) \right] \\ &= \mathbb{E}_{S} \left[ \sup_{g \in \mathcal{G}} \mathbb{E}_{S'} \left[ \widehat{\mathbb{E}}_{S'}(g) - \widehat{\mathbb{E}}_S (g) \right] \right] \\ &\le \mathbb{E}_{S, S'} \left[ \sup_{g \in \mathcal{G}} (\widehat{\mathbb{E}}_{S'}[g] - \widehat{\mathbb{E}}_S[g]) \right] \\ &= \mathbb{E}_{S, S'} \left[ \sup_{g \in \mathcal{G}} \frac{1}{m} \sum_{i=1}^m (g(\mathbf{z}'_i) - g(\mathbf{z}_i)) \right] \\ &= \mathbb{E}_{S, S', \mathbf{\sigma}} \left[ \sup_{g \in \mathcal{G}} \frac{1}{m} \sum_{i=1}^m \sigma_i (g(\mathbf{z}'_i) - g(\mathbf{z}_i)) \right] \\ &\le \mathbb{E}_{\mathbf{\sigma}, S, S'} \left[ \sup_{g \in \mathcal{G}} \frac{1}{m} \sum_{i=1}^m \sigma_i g(\mathbf{z}'_i) + \sup_{g \in \mathcal{G}} \frac{1}{m} \sum_{i=1}^m -\sigma_i g(\mathbf{z}_i) \right] \\ &= \mathbb{E}_{\mathbf{\sigma}, S'} \left[ \sup_{g \in \mathcal{G}} \frac{1}{m} \sum_{i=1}^m \sigma_i g(\mathbf{z}'_i) \right] + \mathbb{E}_{\mathbf{\sigma}, S} \left[ \sup_{g \in \mathcal{G}} \frac{1}{m} \sum_{i=1}^m \sigma_i g(\mathbf{z}_i) \right] \\ &= \mathbb{E}_{\mathbf{\sigma}, S'}[\hat{\mathfrak{R}}_{S'}(\mathcal{G})] + \mathbb{E}_{\mathbf{\sigma}, S}[\hat{\mathfrak{R}}_S(\mathcal{G})] \\ &= 2 \mathfrak{R}_m (\mathcal{G}) \end{align*}\]

증명 과정에서 다음과 같은 사실들이 사용 되었다.

• $\mathbb{E}[g] = \mathbb{E}{S’} \left[ \widehat{\mathbb{E}}{S’} (g) \right]$
• Rademacher variable $\sigma_i$: uniformly distributed independent random variable from $\lbrace -1, +1\rbrace$
• $\mathbb{E}{S’}[\hat{\mathfrak{R}}{S’}(\mathcal{G})] = \mathbb{E}_{S}[\hat{\mathfrak{R}}_S(\mathcal{G})]$: 어차피 random variable이기때문에 기대값(expectation)에 영향을 주지 않음

자잘한 계산을 거치면, 결국 원래 증명하고자 했던 이 식이 나오게된다.

\[\begin{align} \mathbb{E}[g(\mathcal{z})] &\leq \dfrac{1}{m} \sum_{i=1}^m g(z_i) + 2 \mathfrak{R}_m (\mathcal{G}) + \sqrt{\dfrac{\log{\dfrac{1}{\delta}}}{2m}} \\ \mathbb{E}[g(\mathcal{z})] &\leq \dfrac{1}{m} \sum_{i=1}^m g(z_i) + 2 \widehat{\mathfrak{R}}_S (\mathcal{G}) + 3\sqrt{\dfrac{\log{\dfrac{2}{\delta}}}{2m}} \end{align}\]

여기서 각 term은 다음과 같은 의미를 지닌다.

• \(\mathbb{E}[g(\mathcal{z})]\) : True risk. 모델의 실제 성능인 test error에 해당한다.
• \(\dfrac{1}{m} \sum_{i=1}^m g(z_i)\) : Empirical risk. 훈련데이터에 대한 평균 손실 즉 training error에 해당한다.
• \(2 \mathfrak{R}_m (\mathcal{G})\) : Rademacher Complexity. 모델의 복잡도를 나타내는 항.
• \(\sqrt{\dfrac{\log{\dfrac{1}{\delta}}}{2m}}\) : Confidence. 확률적인 신뢰도를 뜻하며, 최소 $1-\delta$의 확률로 이 generalization bound가 성립한다라는 것을 의미. 샘플 크기 $m$이 클 수록 이 값은 작아져서 상한선이 더욱 타이트해짐.

결론은 이렇다. training error(학습이 잘 되었다고 가정)와 test error를 차이를 줄이려면 다음 조건이 필요하다.

1. Rademacher Complexity를 줄인다 = 모델의 복잡도를 줄인다
2. Confidence term을 줄인다 = 데이터를 늘린다

하지만 Rademacher Complexity는 $\mathfrak{R}_m (\mathcal{G})$ 즉, $\mathcal{G}$에 영향을 받는 함수이고, 이는 함수 공간의 크기 $\mathcal{G}$에 영향을 받는 값이라고 알 수 있다.

Norm

위 섹션의 결과는 일반화를 위해서는 훈련의 품질을 높이고 데이터의 양을 늘리는 것도 중요하지만, 함수 공간의 크기를 줄여야한다라는 결론에 도달한다. 그러면 신경망 모델에서 함수 공간의 크기라는 추상적인 개념을 구체적으로 어떻게 측정할 수 있는가?라는 질문에 또다시 봉착하게 된다. 그 답이 바로 모델을 구성하는 파라미터의 “Norm”이다.

Norm은 벡터나 행렬뿐 아니라 함수 공간에 존재하는 원소들까지 일정한 기준(norm)에 따라 크기를 측정하는 추상화된 거리 함수다. 즉, Norm은 다양한 형태의 공간에서 ‘크기’라는 개념을 일관된 방식으로 정의하기 위한 수학적 도구다.

Definition of Norm

다음 조건을 만족할 때 norm이라고 할 수 있다.

1. 양의 정부호 (Positive Definiteness): 0벡터만 길이가 0

   \[\| x \| = 0 \iff x=0\]

2. 동차성 (Homogeneity / Scalar Multiplication): 스칼라배를 하면 크기도 그 절댓값만큼 변함

   \[\| \alpha x \| = 0 = |\alpha| \| x \|\]

3. 삼각 부등식 (Triangle Inequality): 두 벡터의 합의 길이는 각 길이의 합보다 크지 않습니다.

   \[\| x + y \| \leq \| x \| + \| y \|\]

Examples of Norm

단순 norm을 설명하기보다 가중치 입장에서의 norm에 대해 설명하고자 한다.

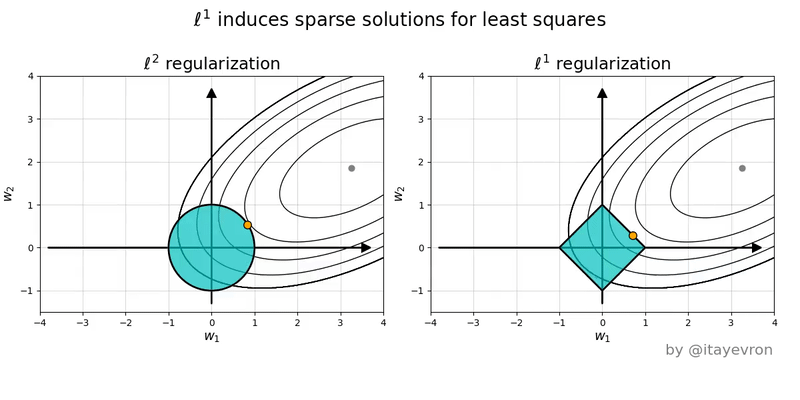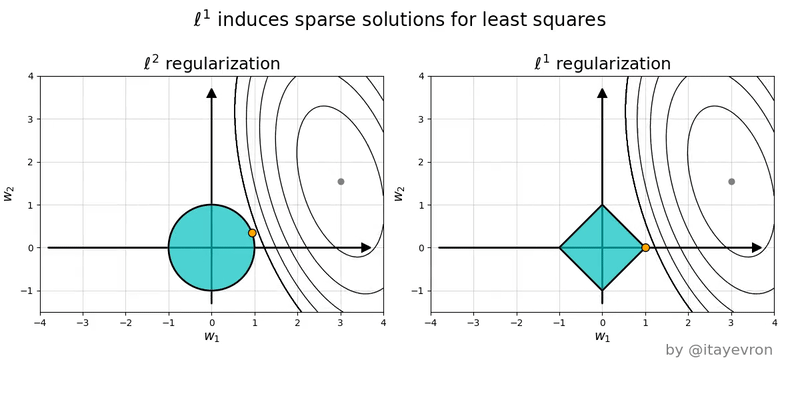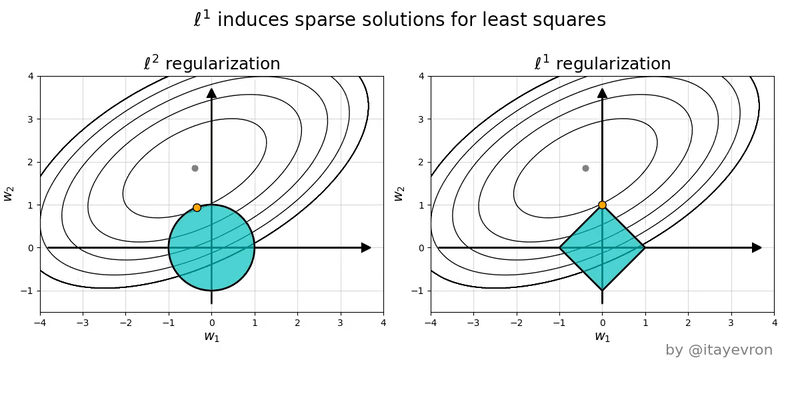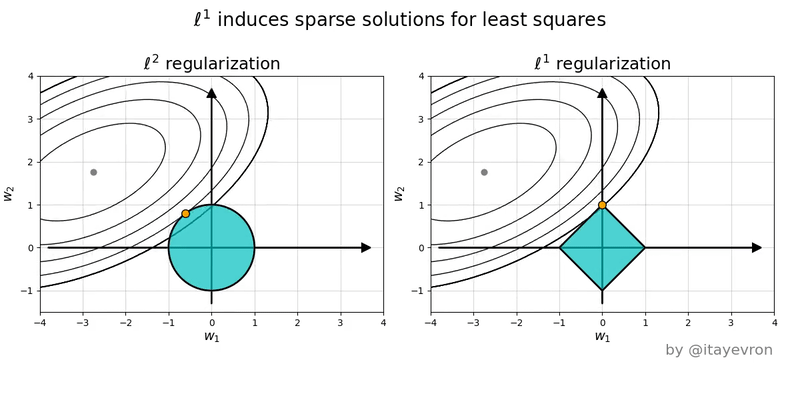
이를 위해 $y = w_1 x_1 + w_2 x_2 + c$형태의 least square problem에서 가중치 공간(weight space)을 기준으로 설명하고자 한다. 위 모델의 가중치 공간에서는 $x, y$축이 $w_1, w_2$이고 $z$ 축은 loss 값이라고 할 수 있다. 이때 각각의 norm은 다음과 같은 의미를 가진다.

L1 Norm (Absolute-value norm)

• 정의: $$|W|_1 = \sum

  w_{ij}

  $$

• 직관:
  • 가중치를 위한 예산의 제약: 모든 가중치의 절대값 총합은 특정 값 혹은 예산(C)를 넘을 수 없다고 제약을 거는것
  • 다이아몬드 형태의 제약: 2차원 가중치 공간에서 $|w_1| + |w_2| \leq C$의 예산조건은 기하하적으로 다이아몬드 형태의 제약을 생성
  • 꼭짓점 효과: loss function의 등고선은 다이아몬드와 만나 최적점을 찾을 때 다이아몬드의 꼭짓점에 닿을 확률이 높음
  • Feature selection 효과: 꼭짓점은 $w_1, w_2$축 위에 있으므로 한 축을 선택하면 다른 축은 0으로 만들어버리는 결과
• 역할: 불필요한 가중치를 정확히 0으로 만들어 희소성(Sparsity)을 유도하고, 이는 곧 피처 선택(Feature Selection) 효과를 발생

L2 Norm (Euclidean Norm)

• 정의: \(\|W\|_F = \sqrt{\sum w_{ij}^2}\)
• 직관:
  • 원점으로부터의 거리 제한: 원점 $(0, 0)$으로부터의 $(w_1, w_2)$까지의 Euclidean distance
  • 원의 형태: $\sqrt{w_1^2 + w_2^2} \leq C$는 가중치 공간에서 원 형태로 존재
  • 원의 효과: 한쪽 축이 아닌 $(w_1, w_2)$ 중간의 어중간한 지점에서 접점 발생
  • weight decay: 모든 축의 퍼센티지에 따른 감쇠효과. 모든 weight을 줄이지만 큰 weight는 더 큰 값으로 줄어드는 효과.
• 역할:
  • 모든 가중치의 크기를 전반적으로 작게 유지하여, 모델이 지나치게 복잡해지는 것을 막고 과적합을 방지하는 부드러운 모델을 생성
  • L1 norm과 달리 파라미터의 크기를 축소할 뿐 파라미터 자체를 제거하지는 않는다. 다른 말로는 파라미터 간의 비율 관계를 바꾸지는 않는다.

L1과 L2 norm은 다음 그림을 같이 보면 이해가 쉽다.

Why does L1 regularization induce sparse models?

Spectral Norm

• 정의: \(\|W\|_\sigma = \max_{\|\mathbf{x}\|_2=1} \|\mathbf{Wx}\|_2\) (최대 특이값)
• 직관:
  • 관점의 전환: L1, L2 Norm이 가중치 벡터의 크기를 봤다면, Spectral Norm은 가중치 행렬 W를 입력 벡터를 다른 벡터로 바꾸는 변환기(Linear Operator)라고 생각하고 행렬의 증폭량을 봄
  • 최대 증폭률(Stretch): 이 변환기가 입력을 최대 몇 배까지 증폭시킬 수 있는가?를 나타냄. 즉, 어떤 방향의 입력이 들어왔을 때 가장 민감하게 반응하여 최대로 길어지는지를 측정
  • 안정성 측정: 이 최대 증폭률이 너무 크면, 입력의 작은 노이즈나 변화에도 출력이 폭발적으로 변하는 불안정한 모델이 됨. 반대로 이 값을 제어하면, 입력이 조금 바뀌어도 출력이 급격히 변하지 않는 안정적인 모델을 만들 수 있음
  • L-$\infty$ Norm은 벡터의 max값을 취한다면, Spectral Norm은 선형변환(matrix)의 크기배율의 최대값을 찾는 문제
  • 즉 Spectral Norm은 SVD를 통해 정의되는 문제로 행렬의 maximum singular value을 찾는 문제로 귀결
  \[\|W\|_\sigma := \sup_{x \neq 0}\dfrac{\| Ax \|_2}{\| x \|_2} = \max_{\| x \|_2=1} \| Ax \|_2\]
• 역할:
  • 함수의 변화율 상한선인 립시츠 상수(Lipschitz Constant)를 직접 제어하여 모델의 안정성을 향상
  • GAN 훈련 시 판별자와 생성자의 학습 균형을 맞추는 역할
  • 적대적 공격(Adversarial Attack)에 대한 방어력을 높이는 역할 수행

Lipschitz Constant

Lipschitz Constant는 함수의 최대 기울기(증가율)을 제한하는 속도 제한 장치같은 역할을 한다. Lipschitz Continuous한 함수 $f$는 입력값 $x_1, x_2$가 변할 때 함수 출력값 $f(x_1), f(x_2)$가 그 입력값의 변화량보다 일정한 상수($K$)배 이상으로 멀어지지 않는다.

\[\begin{align} |f(x_1) - f(x_2)| \leq K |x_1 - x_2| \end{align}\]

신경망에서는 특정 Layer의 spectral norm값이 그 레이어의 lipschitz constant역할을 한다.

Regularization in Practice

앞서 살펴본 Norm들은 모델의 복잡도를 제한하는 정규화(Regularization)의 수학적 기반이다. 이제 실제 딥러NING 모델 학습 시 이 원리가 어떻게 적용되는지 대표적인 두 가지 기법을 통해 알아보도록 하겠다.

특히 이 파트는 (민재식 2025)의 레슨 5. 엇나가는 학습 모델을 어떻게 제어하나의 내용을 많이 참고하였다.

Weight Decay

실은 지금까지 정규화(Regularization) 방법으로 weight decay에 관한 얘기를 계속해서 해왔다. 일반화 오류를 줄이기 위해 모델의 복잡도를 줄여야했고, 모델의 복잡도를 신경망에서 측정하기 위해서 norm을 설명했다. Norm을 통해 측정된 모델의 복잡도는 Loss function에 넣어 loss와 함께 학습과정에서 minimize시키도록 한다.

이러한 접근법을 가중치 감쇠(Weight Decay)라고 부르며, 어떤 Norm을 사용하느냐에 따라 모델에 미치는 영향과 목적이 달라진다.

\[L(W) = L_{\textrm{data}} (W)+ \lambda R(W)\]

이 때 각각은 다음의 의미를 가진다.

• $L(W)$: 최종적으로 최소화해야 할 전체 loss function
• $L_{\textrm{data}}$: 데이터에 대한 loss function (Original loss)
• $\lambda$: 정규화의 강도를 조절하는 하이퍼파라미터
• $R(W)$: 정규화 항(Regularization Term), $| W|^2_2$ 혹은 $| W|_1$

Ridge Regularization (L2 Norm)

\[L(W) = L_{\textrm{data}} (W)+ \lambda \| W\|^2_2\]

앞서 말한 것처럼 일정한 비율(%)로 weight를 감소시켜 모든 weight의 절대적인 크기를 줄인다. Weight vector의 방향을 바꾸지 않고 크기만 줄이는 것이다. 이를 통해 자연스럽게 함수 전체의 기울기가 낮아지고, 특정 feature 하나에 크게 의존하지 않는 robust한 모델이 탄생하게 된다. Robust하다는 것은 덜 예민하다라는 것이고, 이를 Smoothing 효과라고 한다.

L2 norm의 제곱을 하는 이유는 $\sqrt{}$를 제거하여 미분을 편하게 하려는 계산상의 목적이 있고, L2 norm에 더욱 큰 페널티를 줘서 weight decay효과를 더 극대화시키려는 목적이 있다.

Lasso Regularization (L1 Norm)

\[L(W) = L_{\textrm{data}} (W)+ \lambda \| W\|_1\]

Norm에서 보여준 것처럼 L1 regularization을 하면 weight에서 일정한 값을 빼는 효과를 준다. 이 때문에 중요도가 낮은 weight들은 빼는 과정에서 0이 되거나 매우 작은 값이 되어버려 수많은 weight 중에서 일부만 살아남는 희소성(sparsity)를 만들게 된다. 이로 인해 feature를 아예 제거하는 feature selection 효과를 가지게 된다.

Regularization based on Spectral Norm

\[L(W) = L_{\textrm{data}} (W)+ \lambda \| W\|_\sigma\]

Spectrum Norm 기반 Regularzation은 weight의 크기 자체보다, weight matrix가 만드는 변환의 안정성에 초점을 맞춘다.

각 레이어의 Lipschitz Constant $K$가 Spectral Norm값과 같기 떄문에 MLP (함수 $f=f_L \circ \dots \circ f_1$)에서는 다음과 같이 레이어별 Lipschitz Constant를 곱하게 된다.

\[\begin{equation*} K_f \leq \sum_{i=1}^L K_{f_i}= \sum_{i=1}^L \| W_i \|_\sigma \end{equation*}\]

위의 loss function을 최소화하는 것은 각 레이어의 spectrum norm을 줄여, 결과적으로 전체 신경망의 Lipschitz constant bound을 직접 제어하는 것을 의미한다. 이는 입력의 작은 변화에 출력이 폭발적으로 변하는 것을 막아 모델을 안정시키는 역할을 한다.

GAN에서는 (Miyato et al. 2018)을 토대로 이 원리를 더 직접적으로 적용한 스펙트럴 정규화(Spectral Normalization)라는 기법을 사용한다.

이는 loss function에 항을 추가하는 대신, 학습 과정에서 매번 weight matrix $W$를 자신의 spectrum norm으로 직접 나누어주는 방식이다.

\[W_{SN} = \dfrac{W}{ \| W_i \|_\sigma}\]

이 방법을 통해 각 레이어 weight matrix의 spectrum norm을 항상 1로 만들어, 판별자(discriminator)의 Lipschitz constant를 1로 강제하는 효과를 만든다.

GAN에서는 학습의 안정성은 판별자(Discriminator)의 성능에 크게 좌우된다. 판별자는 생성자에게 유의미한 피드백을 주기 위해 입력의 미세한 차이에 민감하게 반응하면서도, 데이터의 다양한 특징(feature)들을 종합적으로 활용해야 한다.

L2 Regularization과 같은 기존 방식들은 여기서 딜레마가 발생한다. (Miyato et al. 2018)에 따르면 기존 방식들은 판별자의 민감도를 높이려는 과정에서 의도치 않게 weight matrix을 low-rank로 만드는 경향이 있다. 행렬의 rank가 낮아진다는 것은 판별자가 소수의 feature에만 의존하게 된다는 의미이며, 이는 결국 생성자에게 질 낮은 피드백을 주게 된다.

반면, SN(Spectral Normalization)은 행렬의 rank와는 독립적으로 오직 최대 singular value(최대 민감도)만을 제어한다. 따라서 판별자가 Lipschitz constant bound를 유지하면서 다양한 feature를 활용할 수 있게 해준다.

Batch Normalization (WIP)

Batch Normalization은 학습 시 미니배치(mini-batch) 단위로 데이터의 평균과 분산을 계산하여 각 레이어의 입력을 정규화하는 방식이다.

Conclusion

지금까지 일반화(Generalization) 성능을 올리기 위해 모델 복잡도를 줄이는 방법을 살펴보았다. 모델의 일반화 성능을 올리기 위해서는 훈련 데이터와 테스트 데이터가 동일분포라고 가정할 때 (1) 충분한 훈련 데이터양을 확보하고 (2) 훈련의 품질을 높여 좋은 모델을 찾아내고 (3) 모델의 복잡도를 낮춰야한다. 이 중 (3)에 집중하여 이론적으로 가설 공간의 크기를 줄이는 것이 모델의 복잡도를 낮추는 역할이다. 특히 신경망에서는 추상적이었던 모델의 복잡도 혹은 가설 공간의 크기는 모델을 구성하는 파라미터들의 Norm으로 실체화시켜서 측정이 가능하다. Norm을 통해 직접적으로 weight를 줄이는 Weight Decay 방법, 그리고 간접적으로 배치의 스케일을 조정하여 간접적으로 weight를 줄이는 Batch Normalization을 알아보았다.

References

• CS260 Machine Learning Algorithms

1. Abu-Mostafa, Yaser S, Malik Magdon-Ismail, and Hsuan-Tien Lin. 2012. Learning from Data. Vol. 4. AMLBook New York.
2. Mohri, Mehryar, Afshin Rostamizadeh, and Ameet Talwalkar. 2018. Foundations of Machine Learning. MIT press.
3. 민재식. 2025. 머신 러닝 마스터 클래스: 기본기를 바로잡는 9가지 레슨. 도서출판 인사이트.
4. Miyato, Takeru, Toshiki Kataoka, Masanori Koyama, and Yuichi Yoshida. 2018. “Spectral Normalization for Generative Adversarial Networks.” ArXiv Preprint ArXiv:1802.05957.